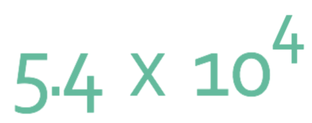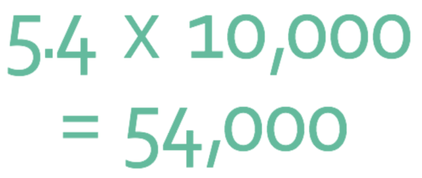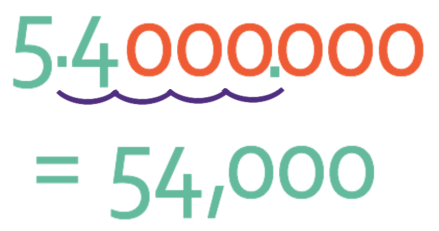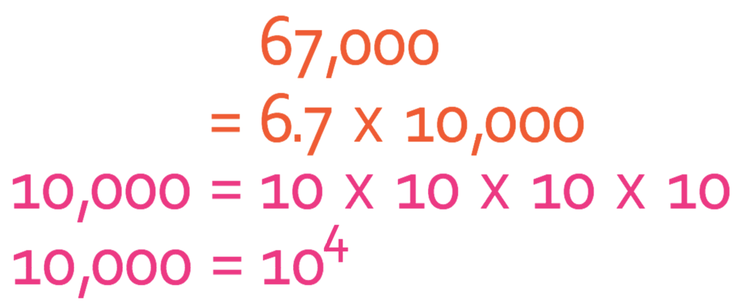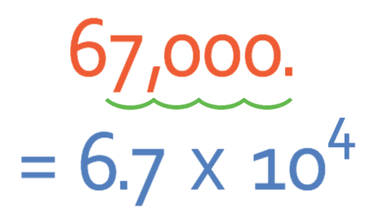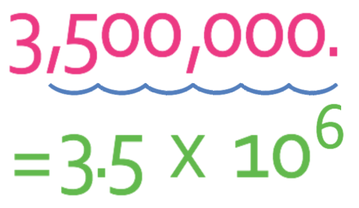1.7 A) Introduction & Large Numbers
Very large and very small numbers can be written in standard form and by writing them in standard form, they are easier to deal with. Scientists often use standard form to measure distances between planets, the speed of waves (e.g. light), the size of atoms etc.
A number written in standard form will have the following structure:
- A is a number between 1 and 10 (1 ≤ A < 10).
- n is the power of 10. It is the number of places that the decimal point moves.
When large numbers are written in standard form, they have a positive value for n. When small numbers are written in standard form, they have a negative value for n. Let’s first look at turning large numbers into standard form.
Large Numbers in Standard Form
When large numbers are written in standard form, they have a positive value for n. This is because the value for A is going to be smaller than the actual value for the number that we are changing into standard form. This means that we have to multiply A by 10 to a positive power in order to get the number that we are converting into standard form.
Let’s start by taking numbers out of standard form
Example 1
Write the number below out of standard form.
A in the number above is 5.4 (and it is between 1 and 10) and n is four; 104 is 10 x 10 x 10 x 10, which is 10,000. We therefore do:
Here are the powers of 10 for positive values of n:
100 = 1
101 = 10
102 = 100
103 = 1,000
104 = 10,000
105 = 100,000
You may find it easier to follow a rule rather than working out what the power of 10 is and then multiplying A by the power of 10. The rule is that we move the decimal point n places to the right for a positive value of n (and if we have a negative value for n, we move the decimal point to the left, which is the case for very small numbers).
To follow the rule, we write the value for A out with many 0’s after the final decimal point.
The value of n for this question is 4, so we move the decimal point 4 places to the right.
The answer is 54,000.
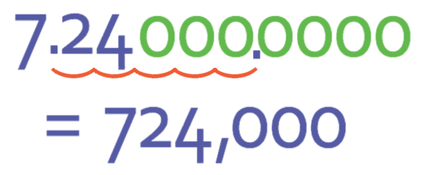
Example 2
Write the number below out of standard form.
The value for n is 5, which means that we are going to be moving the decimal point 5 places to the right. Therefore, we write the value of A down with a load of 0’s after the 4 (the hundredths) and we move the point 5 places to the right.
The answer is 724,000.
Placing a Large Number into Standard Form
We are now going to have a few different examples of placing numbers into standard form. When we are placing numbers into standard form, we need to ensure that we follow the rule of standard form, which is that the value of A must satisfy 1 ≤ A < 10.
Example 3
Write the number below in standard form.
The first step is to find a value for A between 1 and 10 (1 ≤ A < 10). For 67,000, the value of A is 6.7. We then find what we multiply 6.7 by to get 67,000.
Therefore;
Another method to find the answer, is to look at how many places the decimal point has moved when we change 67,000 into 6.7. We can see that the decimal point has moved by 4 places, thus meaning that our answer for n is 4.
Example 4
Write the number below in standard form.
The value of A for this number is 3.5. In order to turn 3,500,000 into 3.5, we move the decimal point 6 places left.
This means that the value for n is 6. Therefore, 3,500,000 written in standard form is 3.5 x 106.
Final note
We are always able to check the answer that we have obtained. If we are placing a number into standard form, we can take our standard form answer out of standard form to see if we obtain the number that we started with. If we are taking something out of standard form, we can check that we have the correct answer by putting the number that we obtained back into standard form.
To save time, you may not want to fully take the number out/ back in to standard form, but it is definitely a good idea to check mentally.