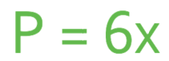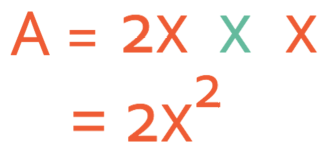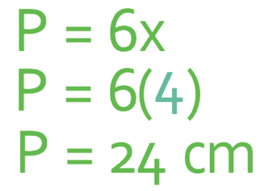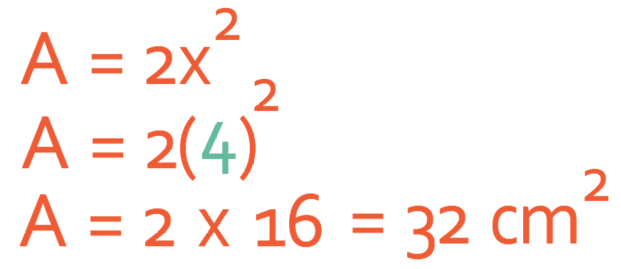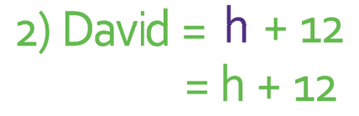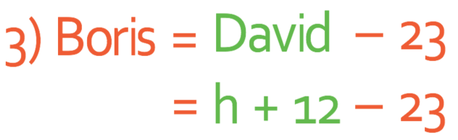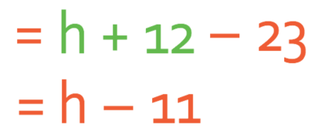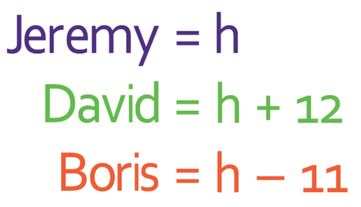Back to Edexcel Algebra Introduction (F) Home
2.1 D) Creating Expressions
2.1 D) Creating Expressions
Often in the exam you will have to create expressions. We create an expression by giving the different variables in the question letters. Let’s have a few examples.
Example 1
I am working for a company and am trying to get people signed up to a loyalty card scheme. For each person that signs up to the scheme, I get paid £2. For each hour that I work, I get paid £6.
Write an expression for this and work out how much I get paid (in pounds) if I work for 3 hours and sign 11 people up.
In order to answer this question, we must represent each of the variables in the question with a letter. There are two variables in the question; the hours that I work and the number of people that I sign up to the loyalty card. I am going to let the letter h be the number of hours that I work, and the letter c be the number of people that I sign up to the loyalty card.
I get paid £6 for every hour that I work and the number of hours that I work is represented by h. Therefore, the amount of money in pounds that I earn purely from hours is calculated by multiplying the number of hours worked (h) by 6, which is 6h.
For each person that signs up to the loyalty card, I get £2. Therefore, my earnings from loyalty card sign ups is the number of people that I sign up (c), multiplied by £2, which is 2c.
My total earnings are the earnings from each of these added together. Therefore, an expression for my total earnings (in pounds) is:
I am working for a company and am trying to get people signed up to a loyalty card scheme. For each person that signs up to the scheme, I get paid £2. For each hour that I work, I get paid £6.
Write an expression for this and work out how much I get paid (in pounds) if I work for 3 hours and sign 11 people up.
In order to answer this question, we must represent each of the variables in the question with a letter. There are two variables in the question; the hours that I work and the number of people that I sign up to the loyalty card. I am going to let the letter h be the number of hours that I work, and the letter c be the number of people that I sign up to the loyalty card.
I get paid £6 for every hour that I work and the number of hours that I work is represented by h. Therefore, the amount of money in pounds that I earn purely from hours is calculated by multiplying the number of hours worked (h) by 6, which is 6h.
For each person that signs up to the loyalty card, I get £2. Therefore, my earnings from loyalty card sign ups is the number of people that I sign up (c), multiplied by £2, which is 2c.
My total earnings are the earnings from each of these added together. Therefore, an expression for my total earnings (in pounds) is:
The second part of our question asks us to work out how much I get paid if I work for 3 hours and sign 11 people up for a loyalty card. I am going to use the expression above to work out how much I have earnt and I will do this by subbing in the values for h and c.
I can now work out my earnings by subbing in these two values into the expression.
- h was the number of hours worked, which is 3 (h = 3)
- c was the number of people that I signed up for a loyalty card, which was 11 (c = 11)
I can now work out my earnings by subbing in these two values into the expression.
Therefore, by working 3 hours and signing 11 people up for loyalty cards, I will earn £40.
Example 2
Expressions are also useful when we are working out the area or perimeter of shapes.
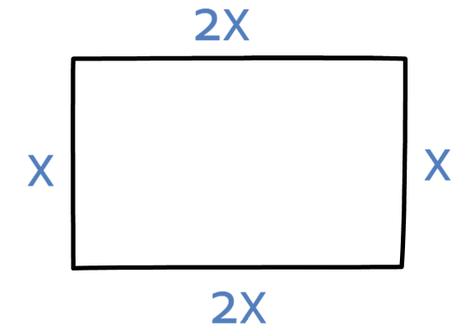
We have a rectangle. The width of the rectangle is twice the length of the height of the rectangle. The height of the rectangle is x cm.
Part 1
Whenever we are working with shapes, it is always best to draw a sketch so that we have a visual representation of what is happening.
The question told us that the height of the rectangle is x. We are also told that the length of the rectangle is twice the length of the height. This means that as the height of the rectangle is x, the length of the rectangle is 2 multiplied by x, which means that the length of the rectangle is 2x.
Expressions are also useful when we are working out the area or perimeter of shapes.
We have a rectangle. The width of the rectangle is twice the length of the height of the rectangle. The height of the rectangle is x cm.
- Find an expression for the perimeter and the area of the rectangle
- Find the perimeter and area of the rectangle when x is 4 cm
Part 1
Whenever we are working with shapes, it is always best to draw a sketch so that we have a visual representation of what is happening.
The question told us that the height of the rectangle is x. We are also told that the length of the rectangle is twice the length of the height. This means that as the height of the rectangle is x, the length of the rectangle is 2 multiplied by x, which means that the length of the rectangle is 2x.
We can now find an expression for the perimeter of the rectangle. The perimeter of a shape is the length of the outside of a shape (it is the distance that you would walk if you were to walk around the outside of a shape). To find the perimeter of a shape, we add the length of all of the sides together. It is best to start at one point on the rectangle and work your way around, so that you do not miss any sides. I am going to start from the top left corner and go clockwise. This means that the perimeter of the above shape is.
We now need to simplify this expression, which we do by adding the x’s together. The terms that are just x can be viewed as 1x; feel free to add in 1’s for these two terms to make it easier to simplify the expression.
The area of a rectangle is calculated by multiplying the length by the height (or width). The length of our rectangle is 2x and the height is x. Therefore, the area of the rectangle is:
We now expressions for both the perimeter and the area of the rectangle above.
Part 2
The second part of the questions asks us to work out the perimeter and area of the shape if x is 4. We do this by subbing in x as 4 into the expressions for the perimeter and area.
The second part of the questions asks us to work out the perimeter and area of the shape if x is 4. We do this by subbing in x as 4 into the expressions for the perimeter and area.
When x is 4, the perimeter of the rectangle is 24 cm and the area is 32 cm2.
Example 3
There are 3 friends; Jeremy, David and Boris. Jeremy has a height of h cm. David is 12 cm taller than Jeremy. Boris is 23 cm smaller than David. Find an expression for the height of David and Boris.
There are 3 friends; Jeremy, David and Boris. Jeremy has a height of h cm. David is 12 cm taller than Jeremy. Boris is 23 cm smaller than David. Find an expression for the height of David and Boris.
Let’s start by finding the height of David. The question tells us that David is 12 cm taller than Jeremy. Jeremy has a height of h, which means that an expression for the height of David is h + 12.
The question also tells us that the Boris is 23 cm smaller than David. Therefore, we can take 23 from the height of David, which is h + 12.
We can simplify this expression by collecting the two numbers that are at the end; 12 – 23 = -11.
Therefore, expressions for the heights are: