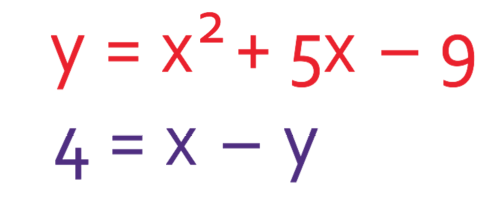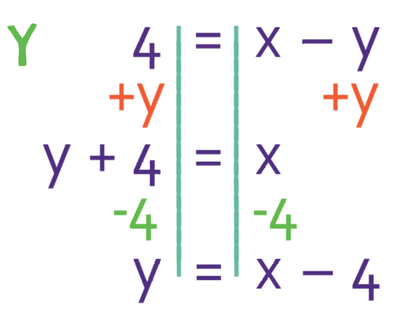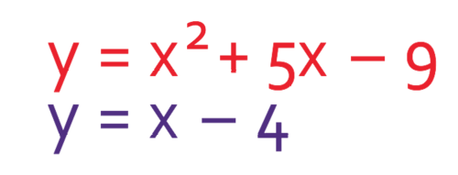Back to Edexcel Simultaneous Equations (F) Home
2.4 D) Quadratic Simultaneous Equations: Graphical Method
2.4 D) Quadratic Simultaneous Equations: Graphical Method
Another method to solve simultaneous equations when one is a linear equation and the other is a quadratic, is to plot them both graphically.
Example 1
Find the values for x and y in the equation below.
Find the values for x and y in the equation below.
We prefer to plot equations when we have y as the subject. This is the case for the first equation, but it is not the case for the second equation. Therefore, the first step is to make y the subject in the second equation.
We now have the two equations:
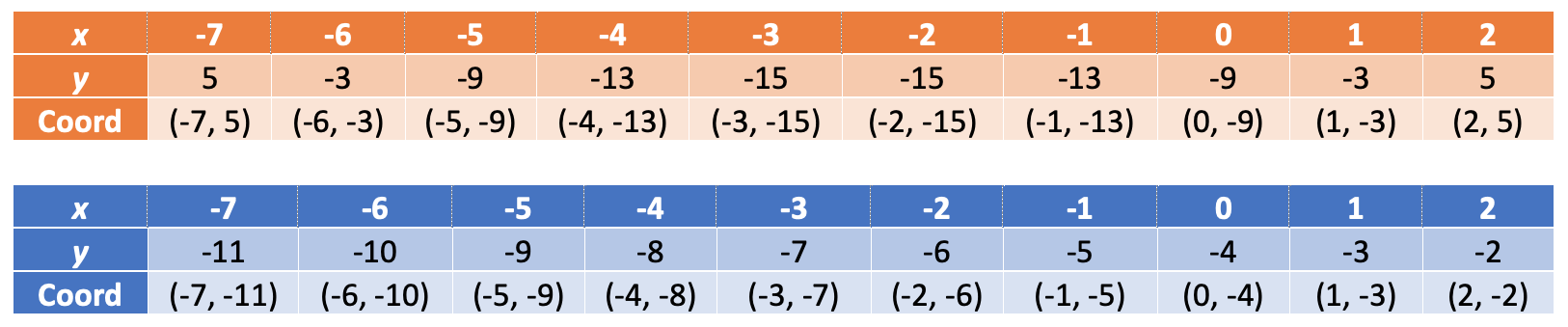
The next step is to plot both of these equations. We can plot these equations by using tables. The tables for the two equations are shown below (click here to learn more about how the tables work for linear equations and click here to learn how the tables work for quadratic equations).
We now use the tables to plot the coordinates and draw the curves. The orange table is for y = x2 + 5x – 9 and the blue table is for y = x – 4.
We now use the tables to plot the coordinates and draw the curves.
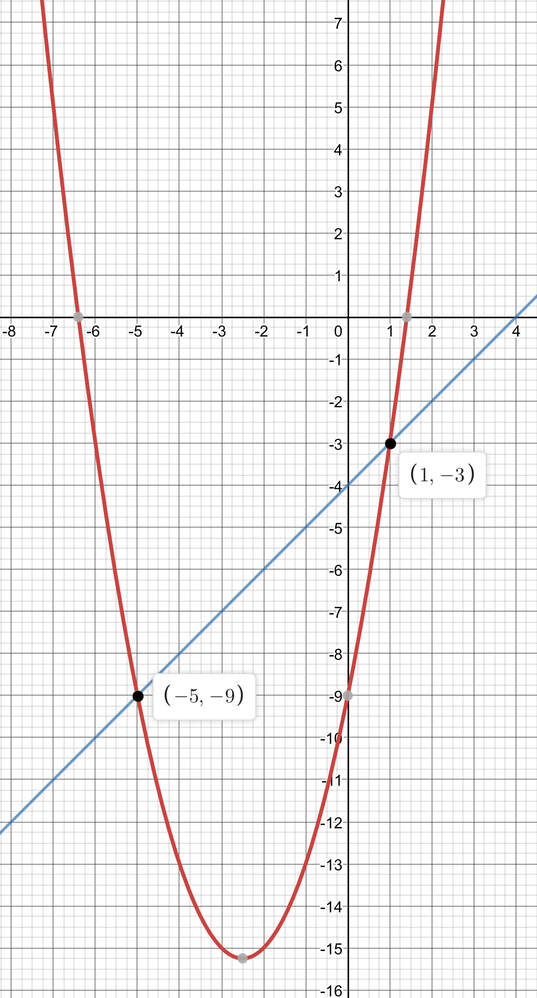
The solutions for the graphical method are where the two graphs intersect one another. The two graphs intersect one another at two different points, and this means that there are two different pairs of solutions for the simultaneous equations. One set of values for x and y are x = -5 and y = -9 (we get these values from the intersection that that is on the left). The second set of values for x and y are x = 1 and y = -3 (these values come from the intersection on the right).
Note for the Exam
It may be the case that in the exam that your answer to simultaneous equations are non-integer numbers (decimals). Do not be alarmed if this is the case. Instead make a rough approximation of what the x and y values are for the point where the graphs intersect one another. There will be a range of values that will be acceptable answers.
There is a question that is like this in the quiz (click here to be taken straight through to the quiz).
It may be the case that in the exam that your answer to simultaneous equations are non-integer numbers (decimals). Do not be alarmed if this is the case. Instead make a rough approximation of what the x and y values are for the point where the graphs intersect one another. There will be a range of values that will be acceptable answers.
There is a question that is like this in the quiz (click here to be taken straight through to the quiz).