Back to Edexcel Linear Graphs (F) Home
2.5 B) Vertical & Horizontal Graphs
2.5 B) Vertical & Horizontal Graphs
Straight line graphs are also known as linear graphs. There are two different types of linear graphs:
In this section, we are going to be looking at vertical and horizontal graphs.
- Vertical and horizontal graphs
- Upwards or downwards sloping graphs
In this section, we are going to be looking at vertical and horizontal graphs.
Vertical Graphs
Verticals lines take the form x = n, where n is a number. With vertical graphs it does not matter what the y value is, because the x coordinate will always be the same (in the example x = n, the x coordinate will always be n, whatever the value of n is).
Verticals lines take the form x = n, where n is a number. With vertical graphs it does not matter what the y value is, because the x coordinate will always be the same (in the example x = n, the x coordinate will always be n, whatever the value of n is).
Example 1
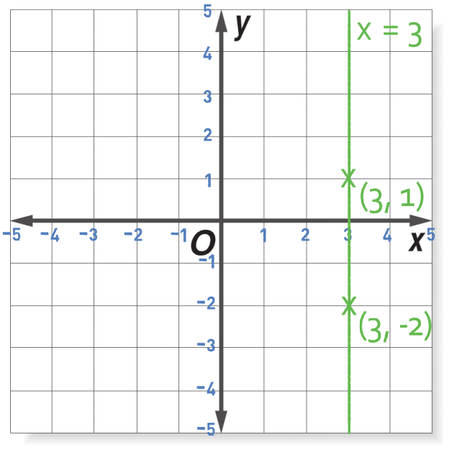
Sketch the graph x = 3.
The x coordinate for this graph is always going to be 3. So, when y is 1, x will be 3, which gives us the coordinates (3, 1). When y is -2, x will also be 3, which means that the coordinates are (3, -2) etc…
In order to plot a linear graph, we need to have two coordinates. We plot these two coordinates on a graph and then draw a line that passes through these two points (it is important to continue the line through both of the points rather than just connecting the two points). The graph for x = 3 is shown below.
Sketch the graph x = 3.
The x coordinate for this graph is always going to be 3. So, when y is 1, x will be 3, which gives us the coordinates (3, 1). When y is -2, x will also be 3, which means that the coordinates are (3, -2) etc…
In order to plot a linear graph, we need to have two coordinates. We plot these two coordinates on a graph and then draw a line that passes through these two points (it is important to continue the line through both of the points rather than just connecting the two points). The graph for x = 3 is shown below.
All of the points that are on the line will have the x coordinate as 3.
Example 2
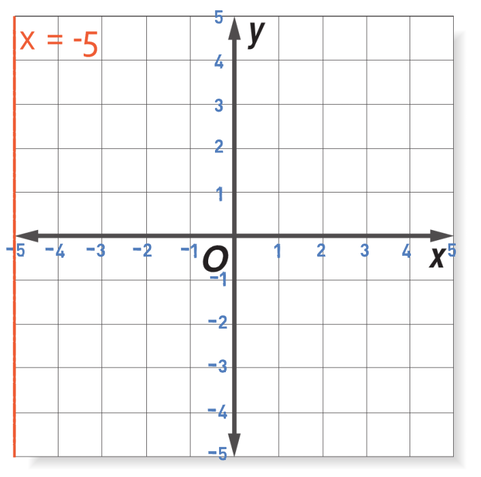
Sketch the graph x = -5.
For graphs that take the form of x = “something”, we do not really need to sub y values in. This is because we know that the graph is going to be vertical, so all we need to do is find -5 on the x axis and then draw a line that is perfectly vertical (going up and down from -5). The graph of x = -5 is shown below.
Sketch the graph x = -5.
For graphs that take the form of x = “something”, we do not really need to sub y values in. This is because we know that the graph is going to be vertical, so all we need to do is find -5 on the x axis and then draw a line that is perfectly vertical (going up and down from -5). The graph of x = -5 is shown below.
Horizontal Graphs
Horizontal graphs take the form y = k, where k is a number. With horizontal graphs it does not matter what the value is for x because the value for y will always be the same. The value for y will be whatever the value for k is.
Horizontal graphs take the form y = k, where k is a number. With horizontal graphs it does not matter what the value is for x because the value for y will always be the same. The value for y will be whatever the value for k is.
Example 3
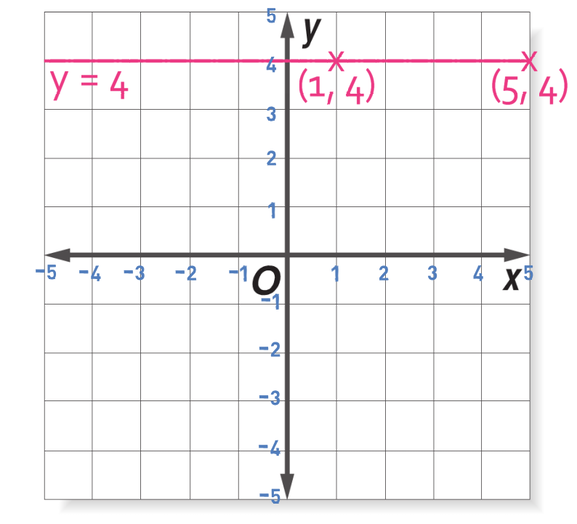
Sketch the graph y = 4.
When x is 1, y will be 4, which gives us the coordinates (1, 4). When x is 5, y will also be 4, which gives us the coordinates (5, 4). We now have two coordinates and as the graph is linear, we can draw a line that passes through both of these points. The graph y = 4 is given below.
Sketch the graph y = 4.
When x is 1, y will be 4, which gives us the coordinates (1, 4). When x is 5, y will also be 4, which gives us the coordinates (5, 4). We now have two coordinates and as the graph is linear, we can draw a line that passes through both of these points. The graph y = 4 is given below.
Example 4
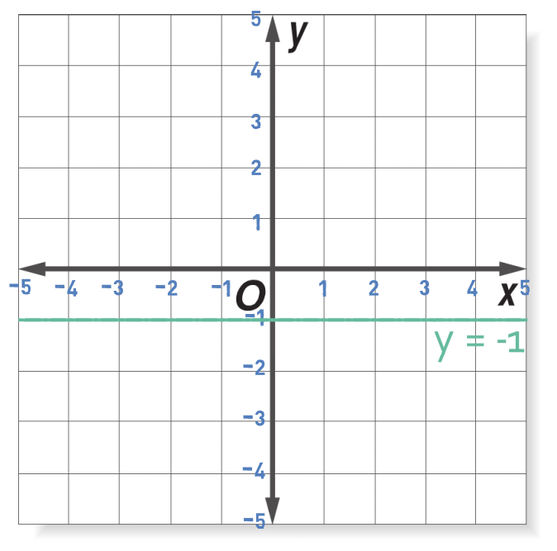
Sketch the graph y = -1
For graphs that are y = “something”, we do not need to sub x values in to find the coordinates. This is because we know that the graph is going to be horizontal and that the y coordinate will always be the value of the “something”, which in this question, the y value will always be -1. Therefore, we can find the point on the axis where y is -1 and draw a horizontal line to the right and left. The graph of y = -1 is shown below.
Sketch the graph y = -1
For graphs that are y = “something”, we do not need to sub x values in to find the coordinates. This is because we know that the graph is going to be horizontal and that the y coordinate will always be the value of the “something”, which in this question, the y value will always be -1. Therefore, we can find the point on the axis where y is -1 and draw a horizontal line to the right and left. The graph of y = -1 is shown below.
Finding the Equation of Vertical and Horizontal Lines
The first step in find the equation of a vertical or horizontal line is to determine whether the line is vertical or horizontal. The next step depends on whether the line is vertical or horizontal:
The first step in find the equation of a vertical or horizontal line is to determine whether the line is vertical or horizontal. The next step depends on whether the line is vertical or horizontal:
- If the line is vertical, we know that the equation will take the form x = n. We find the value of n by looking for the x value where the line passes through the x axis.
- If the line is horizontal, we know that the equation will take the form y = k. We find the value of k by looking for the y value where the line passes through the y axis.
Example 5
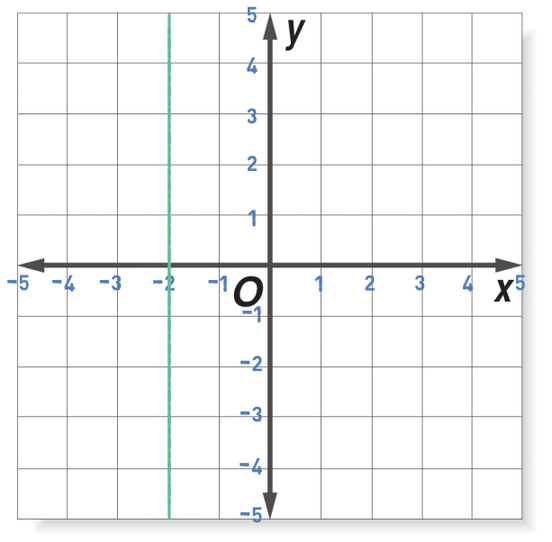
Find the equation of the line on the graph below.
Find the equation of the line on the graph below.
This is a vertical line, which means that the equation will take the form x = n. The value of n is the x coordinate for where the line passes through the x axis. This line passes through the x axis at -2, which means that n is -2. Therefore, the equation for the line is x = -2.
Example 6
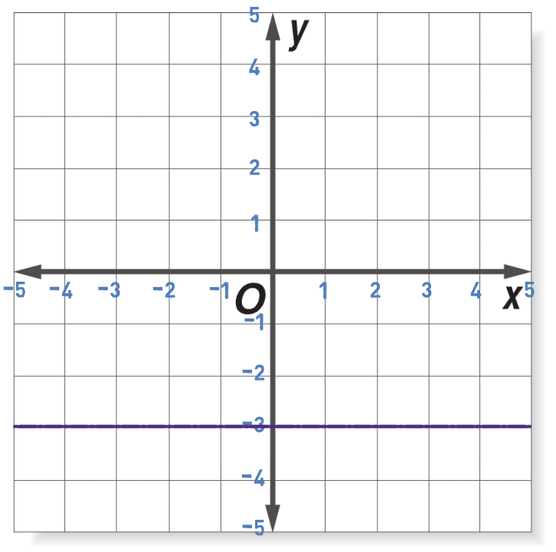
Find the equation of the line on the graph below.
Find the equation of the line on the graph below.
This is a horizontal line, which means that the equation will take the form y = k. The value of k is the y coordinate for where the line passes through the y axis. This line passes through the y axis at -3, which means that k is -3. Therefore, the equation for the line is y = -3.