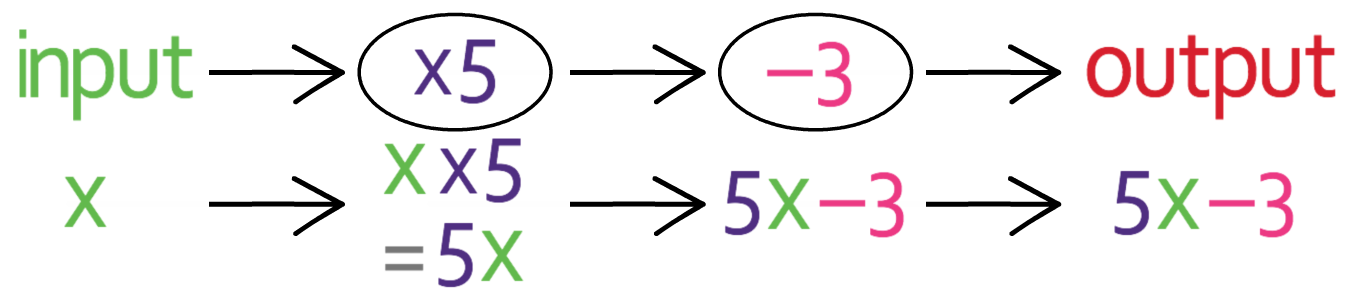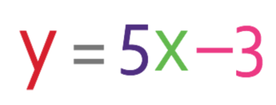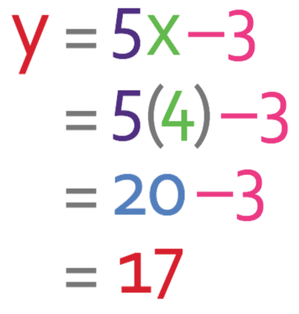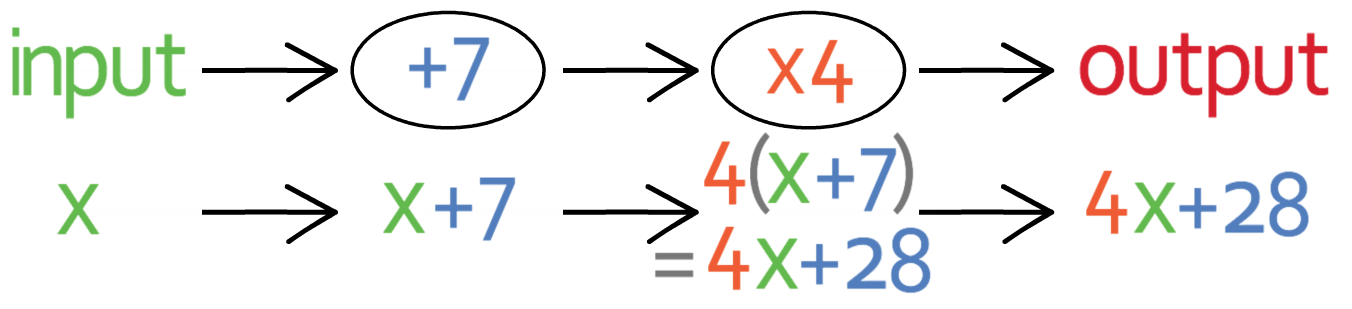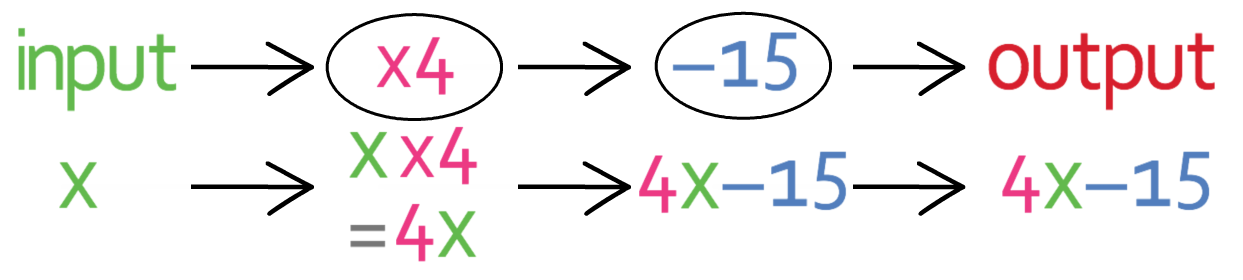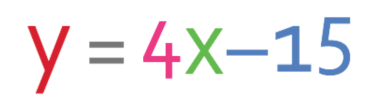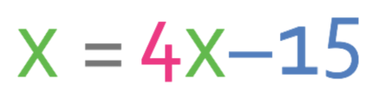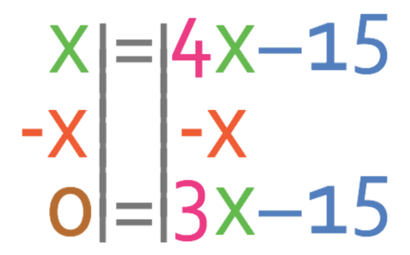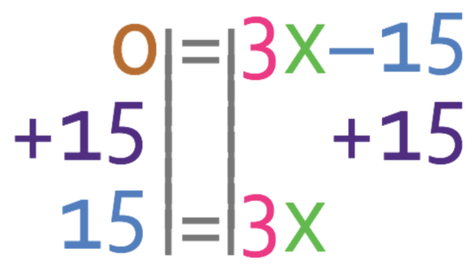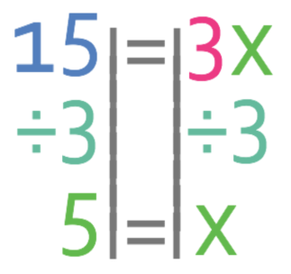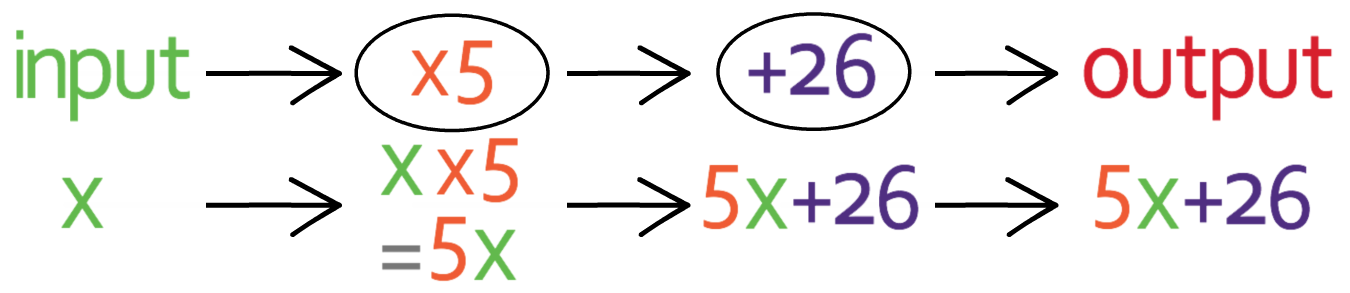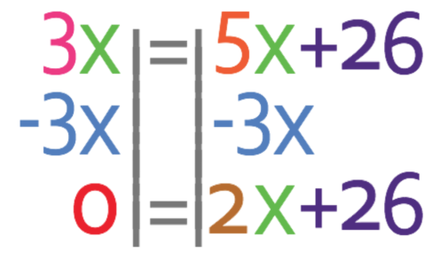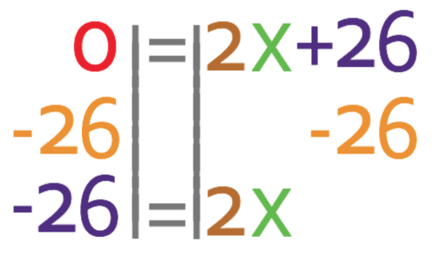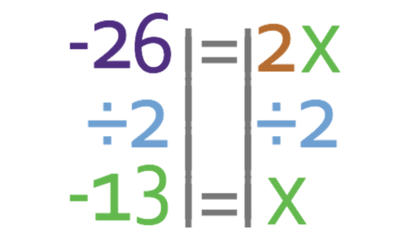Back to Edexcel Functions (F) Home
2.9 B) Functions Machines – Part 2
2.9 B) Functions Machines – Part 2
The content in this section builds on the content that was discussed in the previous section. Therefore, make sure that you have covered the content in the previous section before working through this section (click here to be taken through to the content in the previous section).
Sometimes with function machine questions, we will be asked to write an equation for the output in terms of the input. When this is the case, we will usually have the input as the variable x and the output as the variable y. We then sub the input (x) into the function machine and carry out the operations in the function machine to find what the output (y) is in terms of the input (x). This will make more sense after we have gone through a few examples.
Sometimes with function machine questions, we will be asked to write an equation for the output in terms of the input. When this is the case, we will usually have the input as the variable x and the output as the variable y. We then sub the input (x) into the function machine and carry out the operations in the function machine to find what the output (y) is in terms of the input (x). This will make more sense after we have gone through a few examples.
Example 1
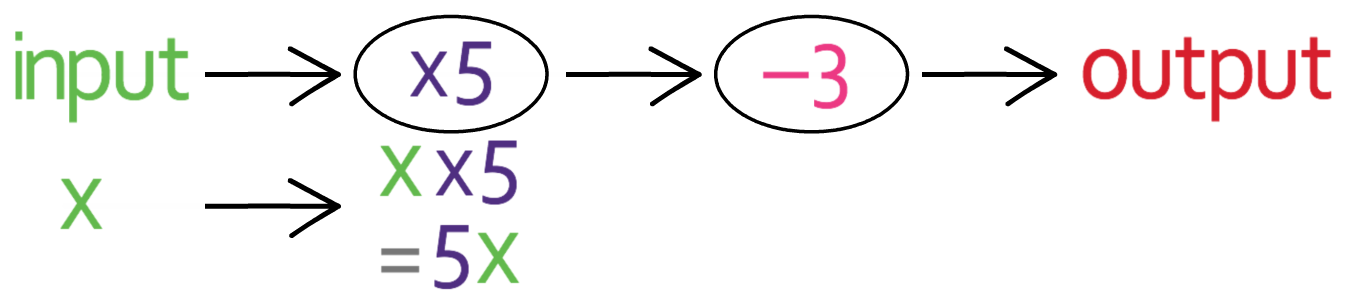
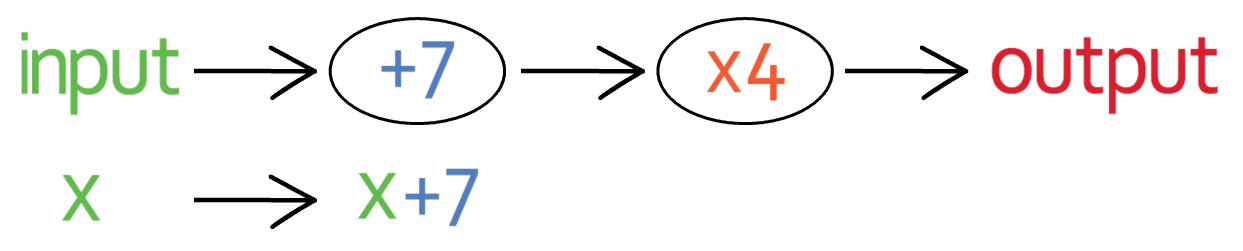
We have the function machine below.
We have the function machine below.
Form an equation for the output of the function in terms of the input (use x as your input and y as your output).
We can form an equation for the output (y) in terms of the input (x) by placing x into the function machine. The first operation in the function machine that we come across is “multiply by 5”, so we multiply our input (x) by 5.
We can form an equation for the output (y) in terms of the input (x) by placing x into the function machine. The first operation in the function machine that we come across is “multiply by 5”, so we multiply our input (x) by 5.
This gives us 5x.
We now complete the second operation in our function machine, which is to “take 3”; we take 3 from 5x.
We now complete the second operation in our function machine, which is to “take 3”; we take 3 from 5x.
This gives us “5x – 3”, which is our output and this output is equal to y. This gives us the equation:
We now have an equation for the output (y) in terms of the input (x).
If we were then given a particular input for the function machine, we can find the output by putting the input into the function machine (in the same way that we did in the previous section), or by subbing the input in as x into the above equation.
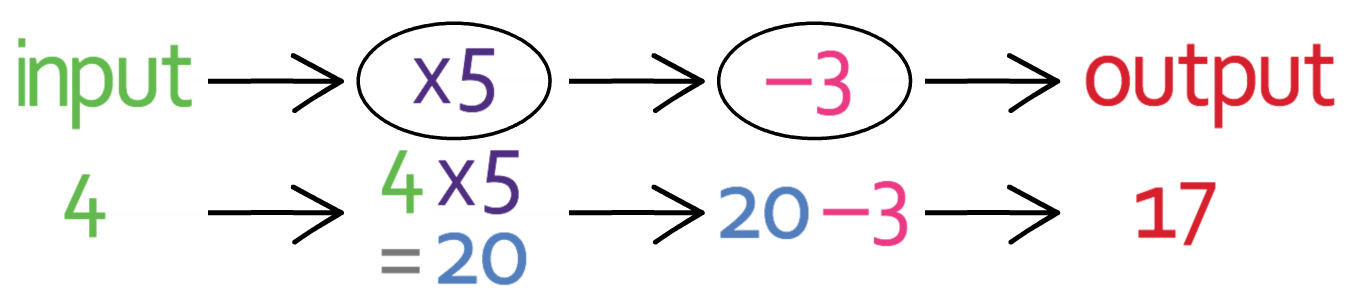
To prove that this is the case, I am going to find the output for the function machine when the input is 4.
Using the Function
We can find the output for the function machine when the input is 4 by placing 4 into the function machine. The working for this is shown below:
If we were then given a particular input for the function machine, we can find the output by putting the input into the function machine (in the same way that we did in the previous section), or by subbing the input in as x into the above equation.
To prove that this is the case, I am going to find the output for the function machine when the input is 4.
Using the Function
We can find the output for the function machine when the input is 4 by placing 4 into the function machine. The working for this is shown below:
The output is 17.
Using the Equation
We can use the equation to find the output for the function machine when the input is 4 by subbing in x as 4 into the equation for the function machine. The working is shown below:
Using the Equation
We can use the equation to find the output for the function machine when the input is 4 by subbing in x as 4 into the equation for the function machine. The working is shown below:
The output for this function (the value of y) is 17, which is the same value that we found when we used the function machine. Therefore, you can see that we can use either of the methods to find the output for the function machine from a given input.
Example 2
We have the function machine below.
We have the function machine below.
Form an equation for the output of the function in terms of the input (use x as your input and y as your output).
We can form an equation for the output (y) in terms of the input (x) by placing x into the function machine. The first operation in the function machine that we come across is “add 7”, so we add 7 to our input (x).
We can form an equation for the output (y) in terms of the input (x) by placing x into the function machine. The first operation in the function machine that we come across is “add 7”, so we add 7 to our input (x).
This gives us x + 7.
We now complete the second operation in our function machine, which is to “multiply by 4”; we multiply “x + 7” by 4. When we multiply “x + 7” by 4, we need to ensure that we multiply both of the terms in “x + 7” by 4. To ensure that I multiply both of the terms in “x + 7” by 4, I am going to place “x + 7” into a bracket. The working is shown below:
We now complete the second operation in our function machine, which is to “multiply by 4”; we multiply “x + 7” by 4. When we multiply “x + 7” by 4, we need to ensure that we multiply both of the terms in “x + 7” by 4. To ensure that I multiply both of the terms in “x + 7” by 4, I am going to place “x + 7” into a bracket. The working is shown below:
This gives us “4x + 28”, which is our output and this output is equal to y. This gives us the equation:
We now have an equation for the output (y) in terms of the input (x).
Example 3
Questions like this can be extended by being told that the input is equal to the output. We answer questions like this by creating an equation for the output in terms of the input. We then replace the output in the equation that we have just created with the value for the input. The final step is to solve the equation to find the value of the input. This will make sense after we have looked at an example.
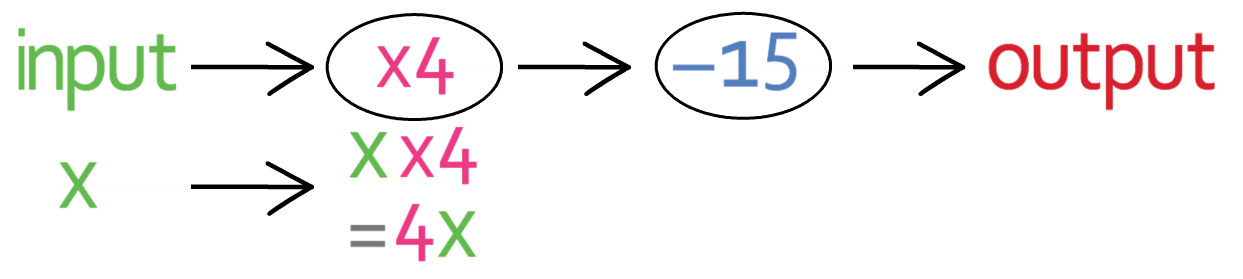
We have the function machine below.
Questions like this can be extended by being told that the input is equal to the output. We answer questions like this by creating an equation for the output in terms of the input. We then replace the output in the equation that we have just created with the value for the input. The final step is to solve the equation to find the value of the input. This will make sense after we have looked at an example.
We have the function machine below.
For a certain input, the output of the function is the same as the input of the function.
Find the value of this input.
The first step in answering this question is to create an equation for the output in terms of the input. I am going to have the input as x and the output as y. We can form an equation for the output (y) in terms of the input (x) by placing x into the function machine. The first operation in the function machine that we come across is “multiply by 4”, so we multiply our input (x) by 4.
Find the value of this input.
The first step in answering this question is to create an equation for the output in terms of the input. I am going to have the input as x and the output as y. We can form an equation for the output (y) in terms of the input (x) by placing x into the function machine. The first operation in the function machine that we come across is “multiply by 4”, so we multiply our input (x) by 4.
This gives us 4x.
We now complete the second operation in our function machine, which is “take 15”; we take 15 from 4x.
We now complete the second operation in our function machine, which is “take 15”; we take 15 from 4x.
This gives us “4x – 15”, which is our output and this output is equal to y. This gives us the equation:
The question told us that the output was equal to the input. This means that x and y are going to be equal to one another. Therefore, we can replace the y on the left side of the equation (the output) with an x (the input). This results in the equation becoming:
We now have an equation with one unknown (x), and this means that we can solve the equation and find the value of x.
There are unknowns on both sides of the equation. When this is the case, we need to get all of the unknowns to one side of the equation and all of the numbers to the other side. We get all of the unknowns to the side that currently has more unknowns. 4x is more than x, so we get all of the unknowns to the right side of the equation, and we get all of the numbers to the left. In order to have all of the unknowns on the right side of the equation, we need to move the x that is currently on the left to the right; we are able to do this by taking x from both sides of the equation.
There are unknowns on both sides of the equation. When this is the case, we need to get all of the unknowns to one side of the equation and all of the numbers to the other side. We get all of the unknowns to the side that currently has more unknowns. 4x is more than x, so we get all of the unknowns to the right side of the equation, and we get all of the numbers to the left. In order to have all of the unknowns on the right side of the equation, we need to move the x that is currently on the left to the right; we are able to do this by taking x from both sides of the equation.
We now need to move the -15 from the right side of the equation to the left. We are able to do this by doing the opposite; we add 15 to both sides.
We want to find the value of x and not 3x. Therefore, we divide both sides of the equation by 3.
This tells us that x is 5, and x was the value for the input. Therefore, the input for this function when the output is the same is 5.
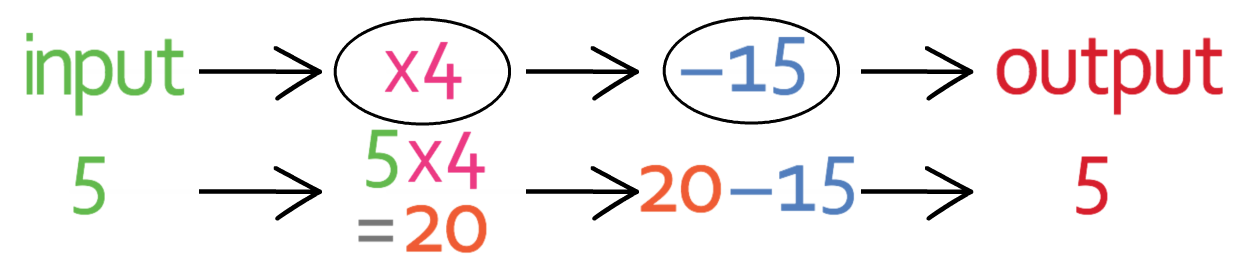
We can check that we have obtained the correct value for the input by placing our answer (5) into the function machine. The working for this is shown below:
We can check that we have obtained the correct value for the input by placing our answer (5) into the function machine. The working for this is shown below:
From the working above, we can see that when we have an input of 5, the output is 5. This means that we have found the correct answer for this question.
Example 4
We have the function machine below.
We have the function machine below.
For a certain input, the output of the function machine is 3 times the input.
Find the value of this input.
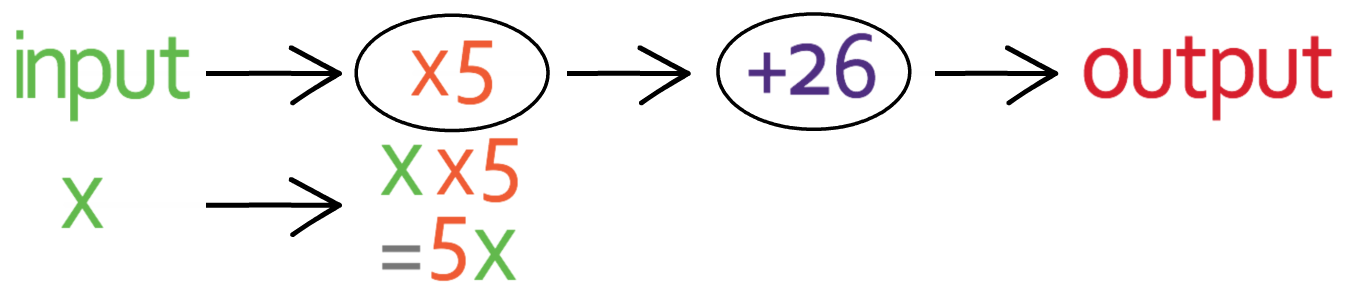
We answer this question in pretty much the same way as the previous question. The first step in answering this question is to create an equation for the output in terms of the input. I am going to have the input as x and the output as y. We can form an equation for the output (y) in terms of the input (x) by placing x into the function machine. The first operation in the function machine that we come across is “multiply by 5”, so we multiply our input (x) by 5.
Find the value of this input.
We answer this question in pretty much the same way as the previous question. The first step in answering this question is to create an equation for the output in terms of the input. I am going to have the input as x and the output as y. We can form an equation for the output (y) in terms of the input (x) by placing x into the function machine. The first operation in the function machine that we come across is “multiply by 5”, so we multiply our input (x) by 5.
This gives us 5x.
We now complete the second operation in our function machine, which is to “add 26”; we add 26 to 5x.
We now complete the second operation in our function machine, which is to “add 26”; we add 26 to 5x.
This gives us “5x + 26”, which is our output and this output is equal to y. This gives us the equation:
We were told in the question that the output is 3 times bigger than the input. I let the output for our function machine be y and our input be x. If the output (y) is 3 times bigger than the input (x), it means that the output in terms of the input is 3x (output = 3 x input = 3 x x = 3x). We can now replace the output (y) in the equation above with 3x. This results in the equation becoming:
We now have an equation that contains just one unknown; the equation only contains x. This means that we can solve the equation to find the value of x.
We find the value of x by getting all of the unknowns to one side of the equation. We get the unknowns to the side of the equation that currently has more unknowns. Currently, there are more unknowns on the right, so we get all of the unknowns to the right side of the equation and all of the numbers to the left. This means that we need to move the 3x from the left side of the equation to the right, and we are able to do this by taking 3x from both sides of the equation.
We find the value of x by getting all of the unknowns to one side of the equation. We get the unknowns to the side of the equation that currently has more unknowns. Currently, there are more unknowns on the right, so we get all of the unknowns to the right side of the equation and all of the numbers to the left. This means that we need to move the 3x from the left side of the equation to the right, and we are able to do this by taking 3x from both sides of the equation.
We now need to move the 26 from the right side of the equation to the left. We are able to do this by doing the opposite. The opposite of adding 26 is taking 26, so we take 26 from both sides of the equation.
We want to find the value of x and not 2x. Therefore, we divide both sides of the equation by 2.
This tells us that x is -13. x is our input, so the input for the function machine when the output is 3 times the input is -13.
If we wanted to check whether we have obtained the correct answer, we could put -13 (the input) into the function machine and then check that the output is 3 times bigger than the input. I am not going to do this, but feel free to do this.
If we wanted to check whether we have obtained the correct answer, we could put -13 (the input) into the function machine and then check that the output is 3 times bigger than the input. I am not going to do this, but feel free to do this.