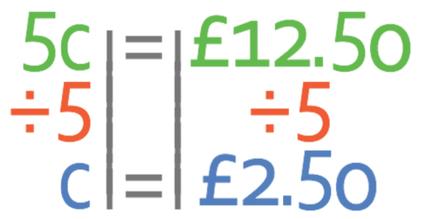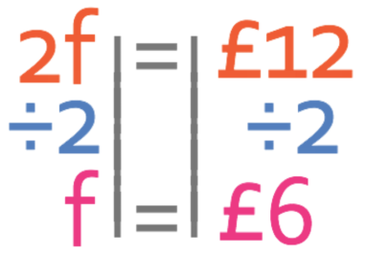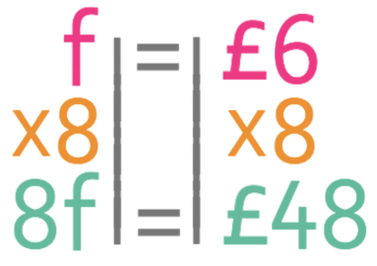Back to Edexcel Direct & Inverse Proportion (F) Home
3.1 C) Direct Proportion
3.1 C) Direct Proportion
Sometimes we are able to describe the relationships between two variables as either directly or inversely proportional to each other.
Direct Proportion
Variables that are in direct proportion move in the same direction and by the same proportion. If one variable was to increase, the other variable would also increase. If one variable was to decrease, the other variable would also decrease. The increase (or decrease) would be in the same proportion. For example, if we were to double one variable, the other variable would also double. If one of the variables was to half, the other variable would also half.
We looked at recipe questions in the previous two sections. The variables in the recipe questions were in direct proportion. This is because the more cakes that we make, the greater the quantity of the ingredients needed. The less cakes that we make, the lower the quantities of the different ingredients needed.
In this section, we are going to be looking at the purchasing of goods. The quantities of the goods purchased and the total cost of all of the goods will be in direct proportion. The more goods that I purchase, the higher the total cost is. The fewer goods that I purchase, the lower the total cost is.
Variables that are in direct proportion move in the same direction and by the same proportion. If one variable was to increase, the other variable would also increase. If one variable was to decrease, the other variable would also decrease. The increase (or decrease) would be in the same proportion. For example, if we were to double one variable, the other variable would also double. If one of the variables was to half, the other variable would also half.
We looked at recipe questions in the previous two sections. The variables in the recipe questions were in direct proportion. This is because the more cakes that we make, the greater the quantity of the ingredients needed. The less cakes that we make, the lower the quantities of the different ingredients needed.
In this section, we are going to be looking at the purchasing of goods. The quantities of the goods purchased and the total cost of all of the goods will be in direct proportion. The more goods that I purchase, the higher the total cost is. The fewer goods that I purchase, the lower the total cost is.
Example 1
I go shopping and buy 5 coffees that cost £12.50. How much would it cost to purchase 3 coffees?
The easiest way to answer questions like this is to use a method known as the unitary method. This method involves working out what the cost of one of the units is. After we have found out how much one-unit costs, we can then work out the cost of the number of units that we are asked for. The question tells us that 5 coffees costs £12.50. I am going to create the following equation from this information; c in the equation below is coffee.
I go shopping and buy 5 coffees that cost £12.50. How much would it cost to purchase 3 coffees?
The easiest way to answer questions like this is to use a method known as the unitary method. This method involves working out what the cost of one of the units is. After we have found out how much one-unit costs, we can then work out the cost of the number of units that we are asked for. The question tells us that 5 coffees costs £12.50. I am going to create the following equation from this information; c in the equation below is coffee.
We want to find out what the price of one coffee is and not what 5 coffees is. Therefore, we need to divide both sides of the equation by 5.
This tells us that each coffee is £2.50.
The question asks us to find the cost of 3 coffees and we are able to do this by multiplying both sides of the equation by 3.
The question asks us to find the cost of 3 coffees and we are able to do this by multiplying both sides of the equation by 3.
Therefore, the cost of 3 coffees is £7.50.
Example 2
It costs £12 to purchase 2 footballs. How much would it cost to purchase 8 footballs?
Like the previous question, I am going to answer this question by using the unitary method. The first step in the unitary method is to work out the cost of 1 of the items. The question tells us that it costs £12 for 2 footballs. Therefore, we can create the following equation from this information; f in the equation below stands for football.
It costs £12 to purchase 2 footballs. How much would it cost to purchase 8 footballs?
Like the previous question, I am going to answer this question by using the unitary method. The first step in the unitary method is to work out the cost of 1 of the items. The question tells us that it costs £12 for 2 footballs. Therefore, we can create the following equation from this information; f in the equation below stands for football.
We want to find the price of one football and not 2 footballs. Therefore, we divide both sides of the equation by 2.
This tells us that a football costs £6.
The question asks us to find the cost of 8 footballs. We are able to do this by multiplying both sides of the equation by 8.
The question asks us to find the cost of 8 footballs. We are able to do this by multiplying both sides of the equation by 8.
Therefore, it costs £48 to purchase the 8 footballs.
Direct Proportion
The variables that we have looked at in both of the examples have been in direct proportion to one another. Direct proportion means that the variables move in the same direction and by the same proportion. As one variable increases, so too does the other variable. And, as one variable decreases, so too does the other variable. Let’s now show that this is the case with the two examples that we looked at.
Example 1
The two different variables in example 1 are the number of coffees and the total cost of the coffees. There were two outcomes with example 1, which I am going to call outcome A and B:
I am now going to compare outcome A and outcome B. When we go from outcome A to outcome B, the number of coffees increases (from 3 to 5) and the total cost of the coffee also increases (from £7.50 to £12.50). These variables are in direct proportion.
Example 2
The two different variables in example 2 were the number of footballs and the total cost of the footballs. There were two outcomes with example 2, which I will call outcome A and B:
I am now going to compare outcome A and outcome B. When we go from outcome A to outcome B, you can see that as the number of footballs purchased increases (from 2 to 8), so too does the total cost of the footballs (from £12 to £48). Also, the variables increase by the same proportion. The number of footballs is 4 times greater in outcome B than A (8 is 4 times bigger than 2) and the total cost of the footballs is 4 times greater in B than A (£48 is 4 times bigger than £12). These variables are in direct proportion.
The variables that we have looked at in both of the examples have been in direct proportion to one another. Direct proportion means that the variables move in the same direction and by the same proportion. As one variable increases, so too does the other variable. And, as one variable decreases, so too does the other variable. Let’s now show that this is the case with the two examples that we looked at.
Example 1
The two different variables in example 1 are the number of coffees and the total cost of the coffees. There were two outcomes with example 1, which I am going to call outcome A and B:
- A) 3 coffees and a total cost of £7.50
- B) 5 coffees and a total cost of £12.50
I am now going to compare outcome A and outcome B. When we go from outcome A to outcome B, the number of coffees increases (from 3 to 5) and the total cost of the coffee also increases (from £7.50 to £12.50). These variables are in direct proportion.
Example 2
The two different variables in example 2 were the number of footballs and the total cost of the footballs. There were two outcomes with example 2, which I will call outcome A and B:
- A) 2 footballs and a total cost of £12
- B) 8 footballs and a total cost of £48
I am now going to compare outcome A and outcome B. When we go from outcome A to outcome B, you can see that as the number of footballs purchased increases (from 2 to 8), so too does the total cost of the footballs (from £12 to £48). Also, the variables increase by the same proportion. The number of footballs is 4 times greater in outcome B than A (8 is 4 times bigger than 2) and the total cost of the footballs is 4 times greater in B than A (£48 is 4 times bigger than £12). These variables are in direct proportion.