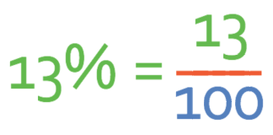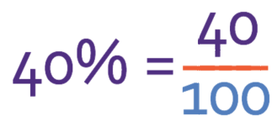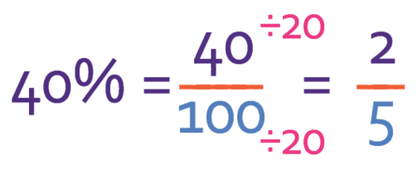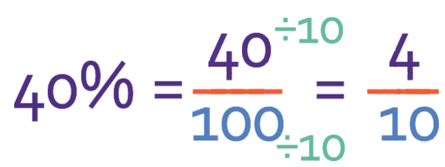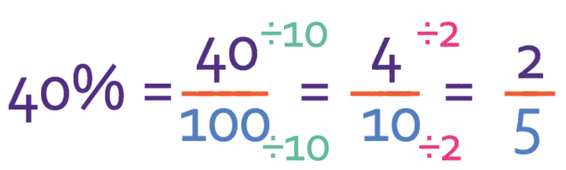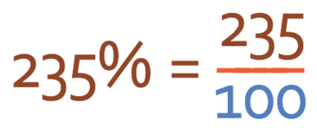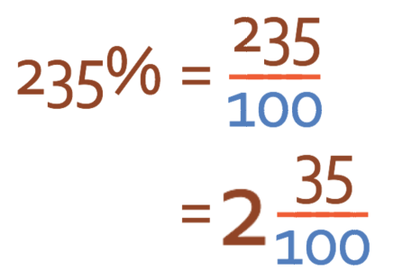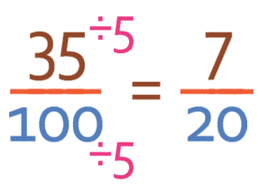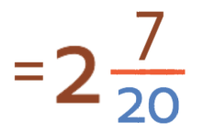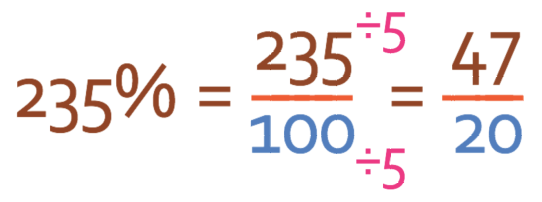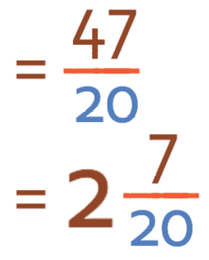Back to Percentage Foundation Home
3.2 B) Converting Percentages into Fractions
3.2 B) Converting Percentages into Fractions
We are easily able to convert percentages into fractions or decimals. Let’s have a look at converting percentages into fractions first.
From the first section, we learnt that percent just means number of parts per 100. We are able to convert a percentage into a fraction by using the percentage that we are converting as the numerator and using 100 as the denominator. This is because percent means per 100.
From the first section, we learnt that percent just means number of parts per 100. We are able to convert a percentage into a fraction by using the percentage that we are converting as the numerator and using 100 as the denominator. This is because percent means per 100.
Example 1
Let’s convert 13% into a fraction.
13% means 13 per 100 and the fraction will be:
Let’s convert 13% into a fraction.
13% means 13 per 100 and the fraction will be:
When we find our fraction, we need to make sure that we simplify it if it is able to be simplified. When we are simplifying fraction, we are looking for any common factors between the numerator and the denominator. We then divide by any common factors. There are no common factors, which means that the fraction is already in its simplest form.
Example 2
Here is another example. Convert 40% into a fraction.
40% means 40 per 100 and we can write this as a fraction as:
Here is another example. Convert 40% into a fraction.
40% means 40 per 100 and we can write this as a fraction as:
This fraction is able to be simplified because 20 is a factor of the numerator (40) and the denominator (100). We therefore divide both the numerator and the denominator by 20.
There are no more common factors between the numerator and the denominator, which means that the fraction is now in its simplest form. 20 was the highest common factor between 40 and 100 and whenever you divide the numerator and the denominator of a fraction by the highest common factor between the numerator and the denominator, you obtain the fraction in its simplest form.
However, when you are simplifying fractions, you do not have to go straight to the final answer. Instead you can divide by any common factors between the numerator and the denominator and then check the fraction that you obtain to see if there are any more common factors between the numerator and the denominator. For example, 10 is factor of both the numerator and the denominator, so let’s divide both the numerator and the denominator by 10. This gives us the fraction:
However, when you are simplifying fractions, you do not have to go straight to the final answer. Instead you can divide by any common factors between the numerator and the denominator and then check the fraction that you obtain to see if there are any more common factors between the numerator and the denominator. For example, 10 is factor of both the numerator and the denominator, so let’s divide both the numerator and the denominator by 10. This gives us the fraction:
We then need to check this to see if there are any more common factors between the numerator and the denominator. When we do this, we see that there is a common factor of 2, which means that we can divide the numerator and denominator by 2. When we do this, we see that the fraction becomes:
When we check this for any more factors, we see that there are no more common factors between 2 and 5, which means that we have found our simplified fraction. This method is slightly longer than the one before, but it is easier if you are dealing with fractions that have trickier numbers in.
1 is equal to 100%. Any percentage that is larger than 100 is going to be an improper fraction, which means that the numerator is going to be greater than the denominator. We can change improper fractions into mixed numbers. Let’s have an example.
Example 3
What is 235% as a fraction?
The process starts the same as before. 235% is 235 per 100, which sounds slightly strange, but it is fine. The percentage that we are finding as a fraction is going to be the numerator and the denominator will be 100. Therefore, our fraction is:
What is 235% as a fraction?
The process starts the same as before. 235% is 235 per 100, which sounds slightly strange, but it is fine. The percentage that we are finding as a fraction is going to be the numerator and the denominator will be 100. Therefore, our fraction is:
The percentage that we were asked to find as a fraction is greater than 100, which means that we will need to write our answer as a mixed number. Also, we need to make sure that our fraction is in its simplest form. We can either convert our improper fraction into a mixed number straight away and then simplify. Or, we can simplify and then convert our improper fraction into a mixed number. I think that it is easier to make our improper fraction a mixed number and then simplify, but I will show you both methods.
Mixed Number then Simplify
The first method is going to be where we convert the improper fraction into a mixed number and then simplify. To convert the improper fraction into a mixed number, we see how many times the denominator goes into the numerator. The denominator of our improper fraction is 100 and the numerator is 235. When we divide 235 by 100, we get 2 remainder 35. Therefore, our mixed number become:
The first method is going to be where we convert the improper fraction into a mixed number and then simplify. To convert the improper fraction into a mixed number, we see how many times the denominator goes into the numerator. The denominator of our improper fraction is 100 and the numerator is 235. When we divide 235 by 100, we get 2 remainder 35. Therefore, our mixed number become:
The next step is to simplify the fraction part of the mixed number and we do this by dividing the numerator and the denominator by the highest common factor between the numerator (35) and the denominator (100). The highest common factor between 35 and 100 is 5, so we divide the numerator and the denominator by 5. This means that the fraction becomes:
Therefore, the final answer is:
Simplify then Mixed Number
I am now going to go through the other method, which is to simplify the improper fraction first and then make the improper fraction a mixed number. We simplify by dividing by the highest common factor, which is 5.
I am now going to go through the other method, which is to simplify the improper fraction first and then make the improper fraction a mixed number. We simplify by dividing by the highest common factor, which is 5.
This is an improper fraction as the numerator is larger than the denominator. We can convert it into a mixed number using the same process as before; seeing how many times the denominator goes into the numerator. We therefore divide 47 by 20, which gives us 2 with a remainder of 7. Our answer is:
This is the same as before. Whenever you are answering questions like this, choose the method that works best for you. There are a few questions like this in the quiz for you to have a go at.