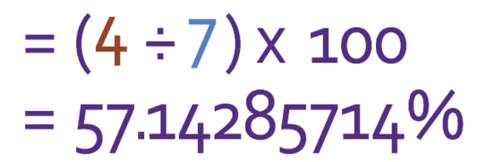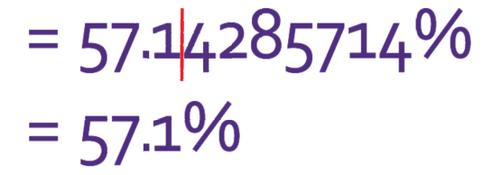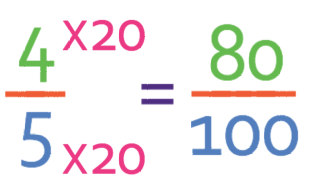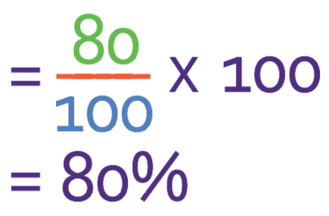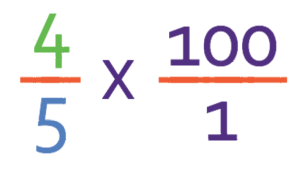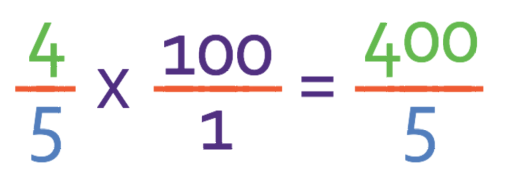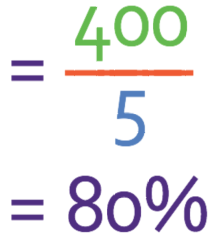Back to Percentage Foundation Home
3.2 C) Converting Fractions into Percentages - Part 1
3.2 C) Converting Fractions into Percentages - Part 1
It is very easy to convert fractions into percentages when we have a calculator. We just insert the fraction into the calculator and multiply by 100. The first example will look at how to convert fractions into percentages when a calculator is present. The second example will look at converting a fraction into a percentage when we are unable to use a calculator.
Example 1
What is the fraction below as a percentage? Give your answer to 1 decimal place.
What is the fraction below as a percentage? Give your answer to 1 decimal place.
We place into the calculator the following operation.
The question asks us to give our answer to 1 decimal place, which means that our answer will be 57.1%.
Example 2
What is the fraction below as a percentage? Do not use a calculator.
What is the fraction below as a percentage? Do not use a calculator.
There are two different methods to working out a percentage as a decimal. The first method is to get the denominator to equal 100. The second method is to multiple our fraction by 100.
Method 1 – Denominator Becoming 100
When we do not have a calculator and are asked to convert a fraction into a decimal, we will be making an equivalent fraction with 100 as the denominator of the new fraction. Currently our denominator of our fraction is 5 and we want to make the denominator 100. This means that we need to multiply the denominator by 20 (we are able to find out what we need to multiply our denominator by to get 100, by dividing the denominator that we want (100) by the current denominator (5), which tells us that we need to multiply our denominator by 20 (100 ÷ 5)). When creating equivalent fractions, we need to make sure that we are multiplying both the numerator and the denominator by the same value and this is so that the value of the fraction does not change meaning that the two fractions are equivalent. If we were to multiply either the numerator or denominator and keep the other one the same, the value of the fraction will change. Therefore, we need to multiple both the numerator and denominator of our fraction by 20.
When we do not have a calculator and are asked to convert a fraction into a decimal, we will be making an equivalent fraction with 100 as the denominator of the new fraction. Currently our denominator of our fraction is 5 and we want to make the denominator 100. This means that we need to multiply the denominator by 20 (we are able to find out what we need to multiply our denominator by to get 100, by dividing the denominator that we want (100) by the current denominator (5), which tells us that we need to multiply our denominator by 20 (100 ÷ 5)). When creating equivalent fractions, we need to make sure that we are multiplying both the numerator and the denominator by the same value and this is so that the value of the fraction does not change meaning that the two fractions are equivalent. If we were to multiply either the numerator or denominator and keep the other one the same, the value of the fraction will change. Therefore, we need to multiple both the numerator and denominator of our fraction by 20.
The next step is to multiply our new fraction that we have obtained by 100.
The dividing by 100 (in the fraction) and the multiplying by 100 cancel each other out, which means that our percentage is the numerator of the fraction. Therefore, the answer 80%.
Method 2 – Multiplying the Fraction by 100
A percentage means “number of parts per 100”. Currently, our fraction is telling us that we have 4 parts per 5. We are able to convert our fraction into a percentage by multiplying our fraction by 100.
A percentage means “number of parts per 100”. Currently, our fraction is telling us that we have 4 parts per 5. We are able to convert our fraction into a percentage by multiplying our fraction by 100.
When we are multiplying an integer (whole number) by a fraction, it may be easier to place the integer over 1.
When multiplying fractions, we multiply straight across; we multiply the two numerators together and we multiply the two denominators together.
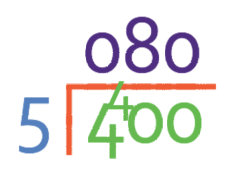
This fraction is an improper fraction because the numerator is greater than the denominator. We can convert this improper fraction into a mixed number by seeing how many times the denominator fully goes into the numerator; we see how many times 5 goes into 400. You might be able to see the answer straight away, but if you can’t you can use the bus stop method to find out what 400 divided by 5 is. The working for the bus stop method is given below and the video has a longer explanation about how the bus stop method works.
We see that our value is 80, and this tells us that our fraction as a percentage is 80%.