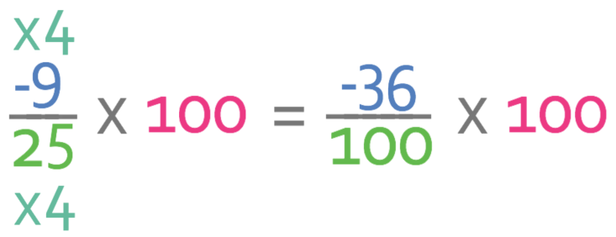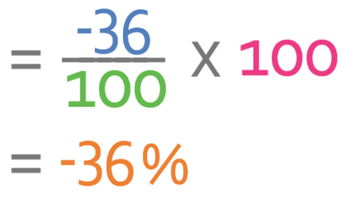Back to Edexcel Percentages (F) Home
3.2 K) Percentage Change
3.2 K) Percentage Change
In real life it is very useful to work out what the percentage change is of something. We use percentage change to see how the prices of assets vary over time. For example, the FTSE 100 was up 2.1% today or the price of Bitcoin rose by 42% over the past month. We also use percentage change to see if we are getting a good deal when we are looking at items in a sale. For example, we are either told or can work out what the percentage change is, which tells us how much we are getting off the items and then we make a decision as to whether this is a good bargain or not.
When we are working out percentage change, we use the following formula:
When we are working out percentage change, we use the following formula:
We are able to find the difference by taking the initial amount away from the final amount.
The formulas above are very easy to use when we have a calculator. When we do not have a calculator, we will use the fraction part of the formula and then make the denominator of the fraction equal 100. It may be the case that you see slightly different versions of this formula. For example, the "final amount" is sometimes referred to as the "new amount".
A positive value for percentage change means that the variable has increased and a negative figure means that the variable has decreased.
Let’s have an example.
A positive value for percentage change means that the variable has increased and a negative figure means that the variable has decreased.
Let’s have an example.
Example 1
At the start of the day, the price of Bitcoin was £6,492. At the end of the day, the price of Bitcoin was £6,879. What was the percentage change? You are able to use a calculator and give your answer to 2 decimal places.
As we are able to use a calculator to work out the percentage change, we just sub the numbers that we are given into the appropriate place in the formula below. We are told in the question that the initial price of Bitcoin is £6,492 and the new price of Bitcoin is £6,879. We sub these values into the formula.
At the start of the day, the price of Bitcoin was £6,492. At the end of the day, the price of Bitcoin was £6,879. What was the percentage change? You are able to use a calculator and give your answer to 2 decimal places.
As we are able to use a calculator to work out the percentage change, we just sub the numbers that we are given into the appropriate place in the formula below. We are told in the question that the initial price of Bitcoin is £6,492 and the new price of Bitcoin is £6,879. We sub these values into the formula.
The question asks us to give our answer to 2 decimal places.
The percentage change is 5.96%. It is always a good idea to look at your answer and see if it makes sense. The percentage change that we have obtained is positive, which means that the value of Bitcoin increased and that is what has happened in the question. Also, a percentage change of 5.96% is quite small and the price of Bitcoin does not change by that much (the price of Bitcoin does change by £387, but as a proportion of the initial price of Bitcoin, this price change is relatively small).
Example 2
A shirt in the sale has a sale price of £16. The non-sale price of the shirt is £25. What is the percentage change? You are not allowed to use a calculator.
We are unable to use a calculator to answer this question, so we are going to get the denominator of the fraction to equal 100. Before we do this, let’s sub the values into their appropriate places in the formula. The initial price of the shirt is £25, and the new price (sale price) is £16.
A shirt in the sale has a sale price of £16. The non-sale price of the shirt is £25. What is the percentage change? You are not allowed to use a calculator.
We are unable to use a calculator to answer this question, so we are going to get the denominator of the fraction to equal 100. Before we do this, let’s sub the values into their appropriate places in the formula. The initial price of the shirt is £25, and the new price (sale price) is £16.
The next step is to create an equivalent fraction with a denominator of 100. In order to find out what we need to multiply the numerator and the denominator of our fraction by, we divide 100 by the current denominator (25), which gives us 4 (100 ÷ 25). We therefore, multiply the numerator and the denominator by 4.
The divide by 100 (from the fraction) and multiply by 100 cancel one another out, which just leaves the numerator as the percentage.
The percentage change is -36%. This is a negative percentage change, which means that the price of the shirt has decreased (which it has).
Example 3
A supermarket wants to work out the percentage change in the sales of meat between two weekends. During the first weekend, the sales of meat was £23,100.63. During the second weekend, the sales of meat was £37,215.22. What is the percentage change in the sales of meat and comment on your answer? Give your answer to 1 decimal place. You are allowed to use a calculator.
We are going to be using the standard formula for working out percentage change to answer this question. The standard formula is:
A supermarket wants to work out the percentage change in the sales of meat between two weekends. During the first weekend, the sales of meat was £23,100.63. During the second weekend, the sales of meat was £37,215.22. What is the percentage change in the sales of meat and comment on your answer? Give your answer to 1 decimal place. You are allowed to use a calculator.
We are going to be using the standard formula for working out percentage change to answer this question. The standard formula is:
The final sales of meat were £37,215.22 and the original sales of meat were £23,100.63. Let’s sub these values into the formula above.
We want to find the answer to 1 decimal place.
The percentage change in meat sales is 61.1%. This is a positive percentage, which means that the sales of meat have increased between the first and second weekend. Also, the percentage change is 61.1%, which means that there was quite a large increase in sales for the second weekend compared to the first weekend.