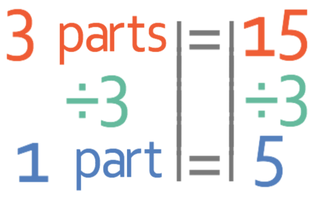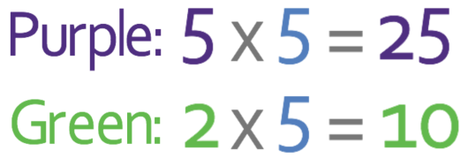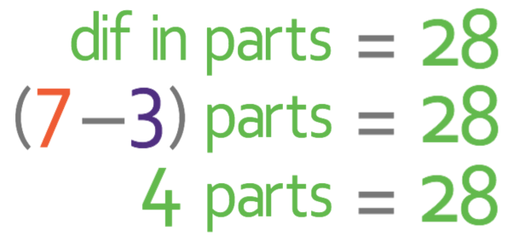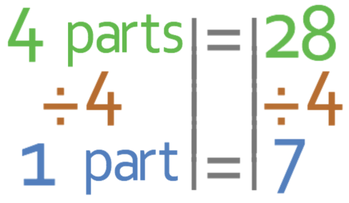Back to Edexcel Ratio (F) Home
3.3 G) Told the Difference
3.3 G) Told the Difference
In the exam, you may be given a ratio and told the difference between the amounts that the different components of the ratio represent. Based on this information, you could be asked to either work out how much each component of the ratio represents or the total amount that has been shared out.
This will all make much more sense when we look through a few examples.
This will all make much more sense when we look through a few examples.
Example 1
I have a bracelet that contains purple and green stones. The ratio of purple stones to green stones in the bracelet is 5 : 2. There are 15 more purple stones than green stones. How many purple stones are there and how many green stones are there?
I have a bracelet that contains purple and green stones. The ratio of purple stones to green stones in the bracelet is 5 : 2. There are 15 more purple stones than green stones. How many purple stones are there and how many green stones are there?
We are told the ratio between the purple and green stones, which is 5 : 2. We are also told that there are 15 more purple stones than there are green stones. In the ratio, we see that there are 5 parts that are purple and 2 parts that are green. From this information, we can see that the difference between the two components of the ratio is 3 parts (5 – 2) and these 3 parts represents the difference between the two stones, which is 15. Therefore, 3 parts of the ratio represents 15 stones, and this gives us the equation below.
We are now able to work out what 1 part of the ratio represent by dividing both sides of the equation above by 3.
Therefore, 1 part in the ratio is 5 stones.
The next step is to multiply the number of parts that are purple and green by the number of stones per part (5). The working is shown below:
The next step is to multiply the number of parts that are purple and green by the number of stones per part (5). The working is shown below:
Therefore, there are 25 purple stones and 10 green stones.
Example 2
I am making orange and pineapple juice. The ratio of oranges to pineapples is 7 : 3. To make my desired quantity of orange and pineapple juice, I am using 28 more oranges than pineapples. How many oranges am I using and how many pineapples am I using?
I am making orange and pineapple juice. The ratio of oranges to pineapples is 7 : 3. To make my desired quantity of orange and pineapple juice, I am using 28 more oranges than pineapples. How many oranges am I using and how many pineapples am I using?
This question tells us that we are using 28 more oranges than pineapples. The question gives us the ratio of oranges to pineapples (7 : 3) and from the ratio, we can see that oranges have 4 more parts than pineapples (oranges have 7 parts and pineapples have 3 parts, so the difference is 4 parts; 7 – 3 = 4). We now know that 4 parts of the ratio represent 28 and from this information we can create the equation below.
We want to find out what 1 part represents, and we do this by dividing the equation above by 7.
This tells us that 1 part is equal to 7.
The next step is to find how many oranges and pineapples we are using by multiplying the number of parts by the amount that 1 part equals (7). The working is shown below:
The next step is to find how many oranges and pineapples we are using by multiplying the number of parts by the amount that 1 part equals (7). The working is shown below:
Therefore, we use 49 oranges and 21 pineapples to make our juice.