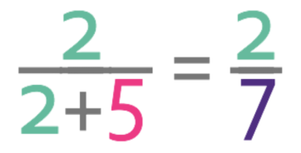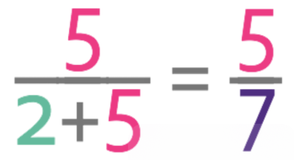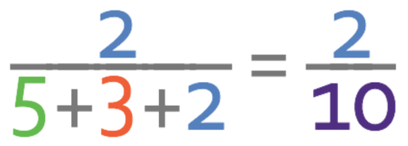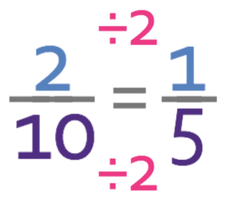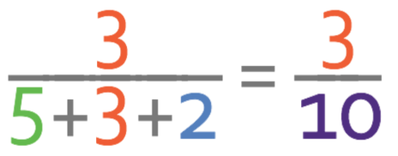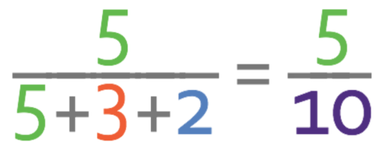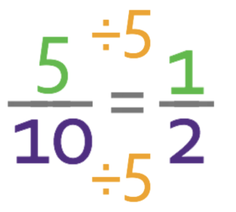3.3 H) Fractions from Ratios – Part 1
Some sweets are shared between Ryan and Sam in the ratio:
b) What fraction of the total sweets does Sam get?
Part a
The first part of this question asks us to work out the fraction of total sweets that Ryan gets. Therefore, the numerator of our fraction will be the number of parts that Ryan has in the ratio. Ryan has 2 parts in the ratio, which means that the numerator of the fraction is 2.
The denominator of the fraction will be the total number of parts in the whole ratio. We work this out by adding all of the parts for the different components in the ratio together; we add 2 and 5, which gives us 7 (2 + 5 = 7). The denominator of the fraction is 7.
We now need to check whether our fraction can be simplified. We check whether a fraction can be simplified by looking for common factors between the numerator and the denominator of the fraction. We then divide both the numerator and the denominator of the fraction by any common factors that we find. There are no common factors between 2 and 7, which means that our fraction is already in its simplest form. Therefore, Ryan gets 2/7 of the sweets.
Part b
We are now onto part b, which is to find the fraction of the total sweets that Sam gets.
The numerator of this fraction will be the number of parts that Sam has in the ratio, which is 5. The denominator of the fraction will be the total number of parts in the ratio, which we found to be 7 in the question before (2+ 5 = 7).
Like before, we need to check that the fraction is in its simplest form. There are no common factors between 5 (the numerator) and 7 (the denominator), which means that the fraction is in its simplest form. Therefore, Sam gets 5/7 of the sweets.
I have a bracelet that has 3 different coloured stones; green, orange and blue. The ratio of green stones to orange stones to blue stones is:
b) What fraction of the total stones in the bracelet are orange?
c) What fraction of the total stones in the bracelet are green?
Part a
This part asks us to work out the fraction of the total stones in the bracelet that are blue.
The numerator of the fraction will be the number of parts in the ratio that are blue, which is 2.
The denominator of the fraction will be the total number of parts in the ratio. We can work out the total number of parts in the ratio by adding all of the different components in the ratio together. The total number of parts in the ratio is 10 (5 + 3 + 2 = 10). The fraction of the total stones in the bracelet that are blue is:
There are no more common factors between the new numerator and the new denominator of the fraction, which means that the fraction is now in its simplest form. Therefore, 1/5 of the stones in the bracelet are blue.
Part b
This part asks us to work out the fraction of the total stones in the bracelet that are orange. The numerator of the fraction will be the number of parts in the ratio that are orange, which is 3. The denominator of the fraction will be the total number of parts in the ratio, which is 10 (we found the total number of parts in the ratio in the previous question by adding up all of the components in the ratio; 5 + 3 + 2 = 10). The fraction of the total stones in the bracelet that are orange is:
There are no common factors in the numerator and the denominator of the fraction, which means that the fraction is in its simplest form. Therefore, 3/10 of the stones in the bracelet are orange.
Part c
The final part asks us to find the fraction of the total stones in the bracelet that are green. The numerator of this fraction will be the number of parts in the ratio that are green, which is 5. The denominator of the fraction will be the total number of parts in the ratio, which is 10. The fraction of the total stones in the bracelet that are green is:
There are no more common factors between the numerator and the denominator, which means that the fraction is in its simplest form. Therefore, 1/2 of the total stones in the bracelet are green.