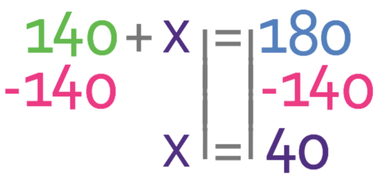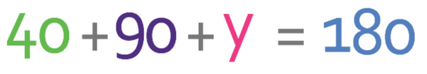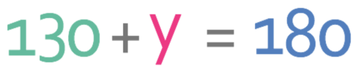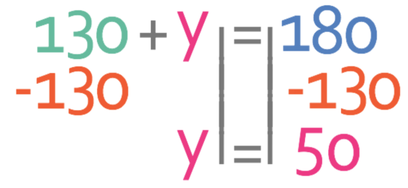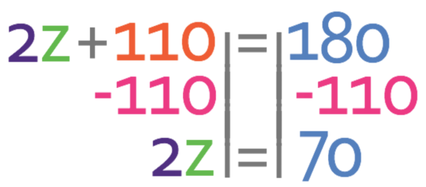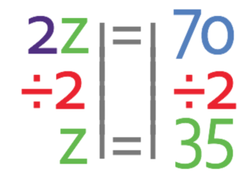Back to Edexcel Angles, Lines & Polygons (F) Home
4.1 A) Triangles
4.1 A) Triangles
In this section, we are going to look at the different types of shapes starting with triangles.
Triangles
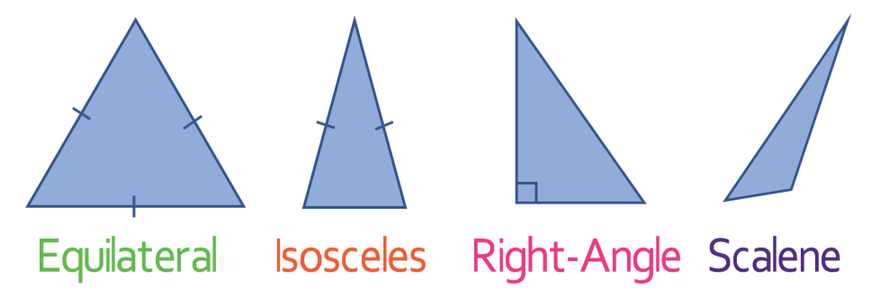
A triangle is a two-dimensional (2D) shape that has 3 sides, 3 angles and 3 vertices (corners/ intersecting lines). All of the angles in a triangle add up to 180°.
There are four different types of triangle; equilateral, isosceles, right-angle and scalene.
A triangle is a two-dimensional (2D) shape that has 3 sides, 3 angles and 3 vertices (corners/ intersecting lines). All of the angles in a triangle add up to 180°.
There are four different types of triangle; equilateral, isosceles, right-angle and scalene.
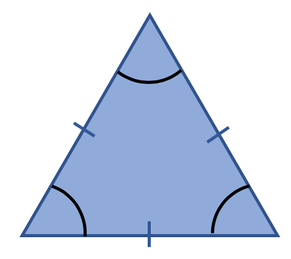
Equilateral Triangle
All of the sides on an equilateral triangle are the same length; we indicate that the sides are the same length by placing a small dash on the line. Equilateral triangles also have angles that are of the same size; all of the angles in an equilateral triangle are 60° (180° ÷ 3).
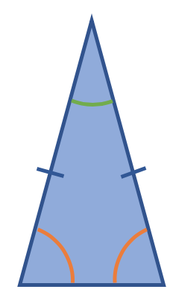
Isosceles Triangle
An isosceles triangle has 2 sides that are the same length (the two sides that are the same length have a dashed line through them). Two of the angles in an isosceles triangle are the same size. These are the two angles between the side that is a different length and the two sides that are the same length. For the above triangle, the bottom two angles are the same (the orange angles).
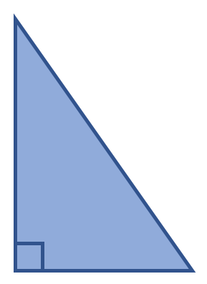
Right-Angle Triangle
A right-angle triangle is a triangle that has right-angle in it (a 90° angle). We indicate that an angle is a right angle by placing a small square box in the right-angle angle.
Scalene Triangle
All of the sides in a scalene triangle are of different lengths. As the lengths are unequal, so are the angles in the triangle.
A Few Examples
We are now going to have a look at a few different triangle examples. The first step in answering the following questions is to first identify what type of triangle we have; is the triangle an equilateral, isosceles, right-angle or scalene? We then use the type of triangle to help us find the size of the unknown angle.
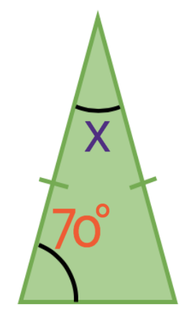
Example 1
What is the size of angle x?
We are now going to have a look at a few different triangle examples. The first step in answering the following questions is to first identify what type of triangle we have; is the triangle an equilateral, isosceles, right-angle or scalene? We then use the type of triangle to help us find the size of the unknown angle.
Example 1
What is the size of angle x?
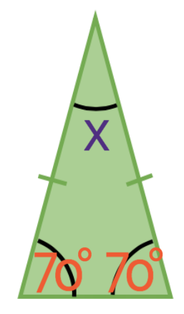
The first step in answering this question is to identify what type of triangle we have. The triangle above is an isosceles triangle. We can tell this because 2 of the lengths in the triangle are the same (the two lengths that are the same have a dash through them). This means that the two angles between the length that is not the same and the lengths that are the same will be the same size; on the triangle above, the two angles at the bottom are the same as one another – they are both 70°.
We now have two angles in the triangle and we know that all of the angles in a triangle add up to 180°. Therefore, we can create the following equation from this information:
We can now solve to find the value of x. The first step in finding the value of x is to collect the numbers on the left side of the equation.
In order to find the value of x, we need to move the 140 from the left side of the equation to the right. We are able to do this by doing the opposite; we take 140 from both sides of the equation.
Therefore, angle x is 40°.
Example 2
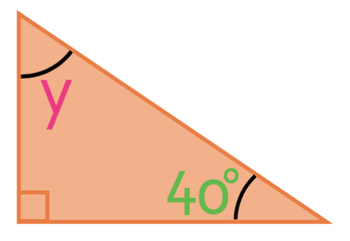
What is the size of angle y in the triangle below?
What is the size of angle y in the triangle below?
The triangle above is a right-angle triangle and we know this because one of the angles has a small box in it. The angles that has a box in it is 90°. We now have two of the angles in the triangle and we know that all of the angles inside a triangle add up to 180°. Therefore, we can create the following equation:
We now solve to find the value of y. The first step is to collect the two numbers on the left side of the equation.
We find the value of y by moving the 130 from the left side of the equation to the right. We are able to do this by taking 130 from both sides of the equation.
Angle y in the triangle above is 50°.
Example 3
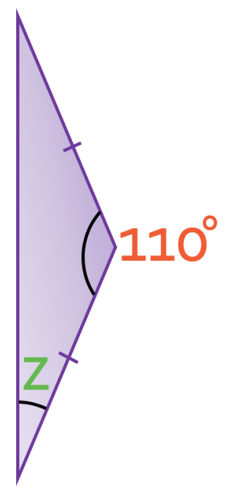
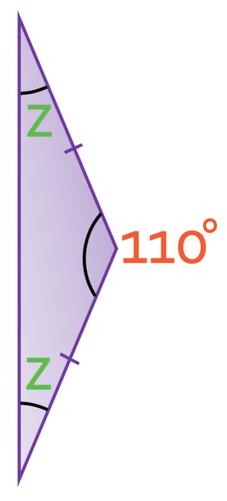
What is the size of angle z in the triangle below?
What is the size of angle z in the triangle below?
The triangle above is an isosceles triangle because two of the lengths are the same (the sides that are the same length have a dash through them). This means that the two angles between the length that is not the same and the lengths that are the same will be the same size; the two angles on the left of this triangle are the same. The bottom left angle is z and we know that this angle will be the same size as the top left angle. Therefore, we can label the top left angle as z as well. The labelled triangle is shown below.
We know that all of the angles in a triangle will add up to 180°. Therefore, we can create the following equation:
We can collect the z’s on the left side of the equation.
We want to find the value of z. We are able to do this by getting all of the z terms to one side of the equation and all of the numbers to the other side of the equation. I am going to get all of the z terms to the left side of the equation and all of the numbers to the right side of the equation. This means that I need to move the 110 from the left side of the equation to the right. I am able to do this by doing the opposite; I take 110 from both sides of the equation.
We want to find the value of z and not 2z. Therefore, we divide both sides of the equation by 2.
This tells us that angle z is 35°.