Back to Edexcel Angles, Lines & Polygons (F) Home
4.1 B) Quadrilaterals – Part 1
4.1 B) Quadrilaterals – Part 1
A quadrilateral is a two-dimensional shape that has 4 sides and 4 angles. All of the angles in a quadrilateral add up to 360°.
Like triangles, there are many different types of quadrilaterals.
Like triangles, there are many different types of quadrilaterals.
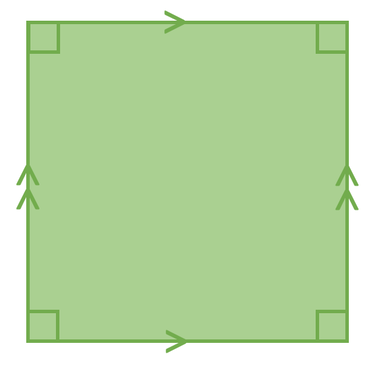
Square
All of the sides in a square are the same length. Also, the opposing sides of a square are parallel to one another. We indicate that sides are parallel to one another by using the sign “>” for the first pair of parallel lines and “>>” for the second pair and so on. All of the four angles in a square are 90°.
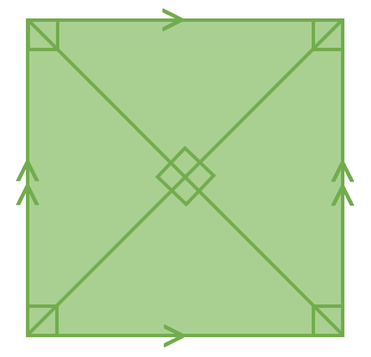
If we were to draw two diagonal lines going from one corner of the square to the opposite corner, the two diagonal lines would intercept each other at 90° (the two diagonal lines will be perpendicular to one another).
If we were to draw two diagonal lines going from one corner of the square to the opposite corner, the two diagonal lines would intercept each other at 90° (the two diagonal lines will be perpendicular to one another).
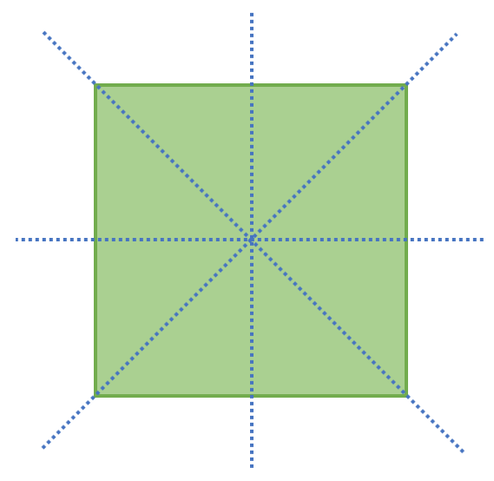
Squares have 4 lines of symmetry; a horizontal line, a vertical line and the two diagonals. The four lines of symmetry are shown on the square below.
Rectangle
The opposite sides in a rectangle are the same length; the top and the bottom are the same length, and the left and the right side are same length. Also, the opposite sides are parallel to one another. Each of the angles in a rectangle is a right angle (90°).
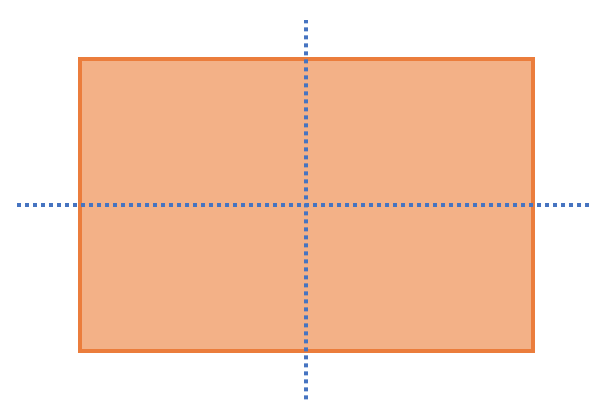
Rectangles have two lines of symmetry; one is horizontal and the other is vertical. These two lines of symmetry are shown on the rectangle below.
Rectangles have two lines of symmetry; one is horizontal and the other is vertical. These two lines of symmetry are shown on the rectangle below.
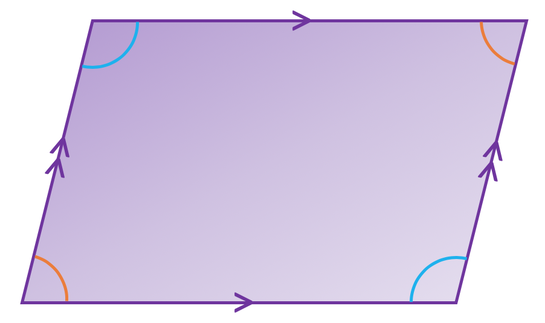
Parallelogram
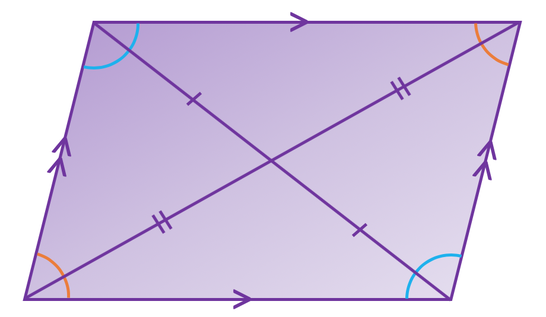
Opposing sides in a parallelogram are the same length and parallel to one another. Also, opposite angles in a parallelogram are the same size and there are two pairs of angles that are the same (top right and bottom left, and top left and bottom right). The diagonal lines bisect one another, which means that they divide each other in half/ meet at the midpoint for each of the lines.
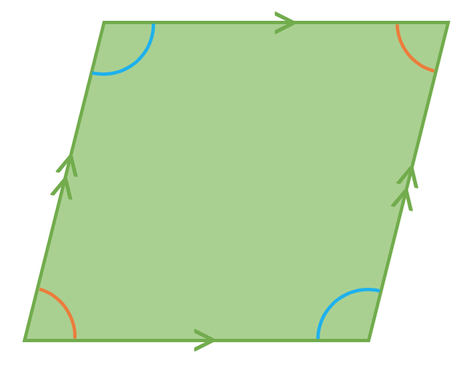
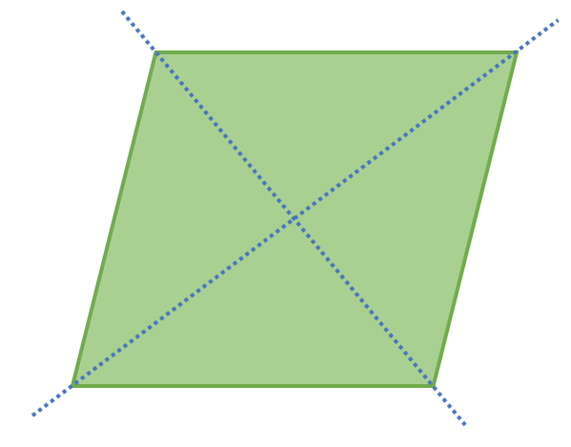
Rhombus
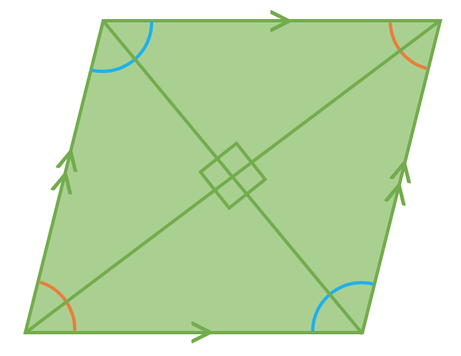
A rhombus is very similar to a parallelogram. The only difference is that all of the sides in a rhombus are of the same length. Opposite sides in a rhombus are parallel and angles that are opposite are the same size. The diagonals (lines going from one corner to the opposite corner) bisect one another at right angles to each other.
Rhombus’ have two lines of symmetry and these lines are the two diagonals. These line of symmetry are shown on the diagram below.
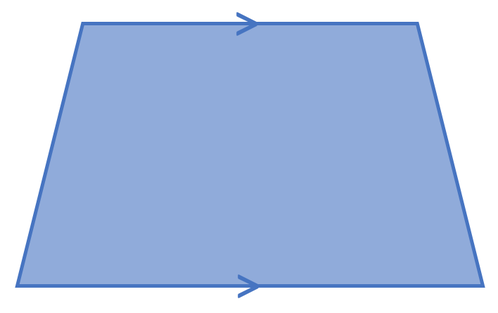
Trapezium
A trapezium has one pair of parallel sides. The sides that are parallel to each other have a “>” on them; on the trapezium above, the top and the bottom are parallel to one another.
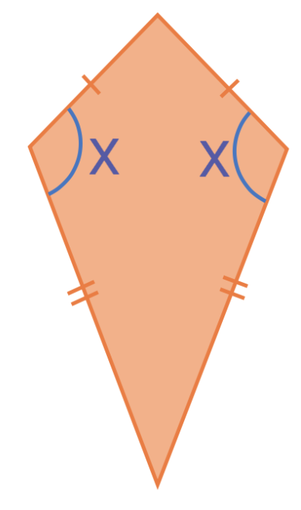
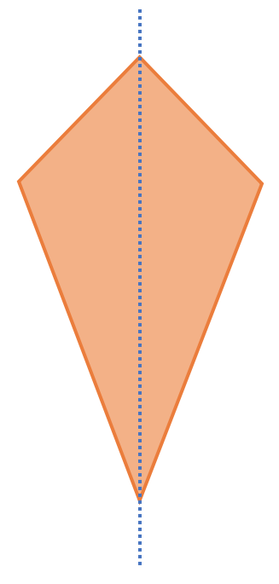
Kite
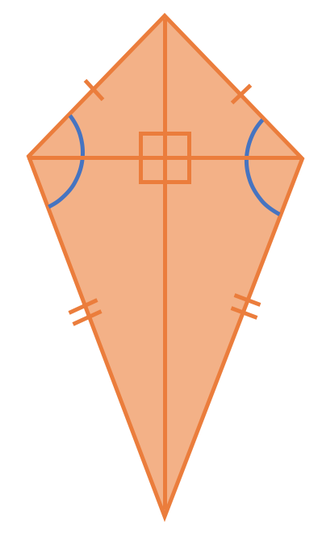
A kite has two pairs of sides that are equal to one another. The sides that are equal to one another are next to each other. For the above kite, the two sides at the top (the top left and top right side) are the same length, and the two sides at the bottom (the bottom left and bottom right side) are the same length. Kites have two angles that are the same and the angles that are the same are the angles that join the sides of different lengths. The two angles that are the same on the above kite are the ones that are labelled x (the middle left and the middle right angle). The diagonals on a kite intersect one another at right angles (90°).
Kites have one line of symmetry. The line of symmetry is the line that passes through the two angles that join the sides that are the same length. The line of symmetry is shown on the kite below.