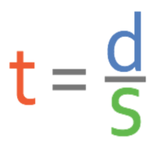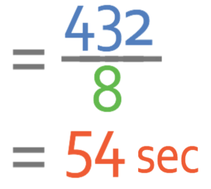Back to Edexcel Unit of Measure (F) Home
4.10 I) Speed – Part 1
4.10 I) Speed – Part 1
Speed is the distance travelled by something in one unit of time. We are able to work out speed by using the calculation below:
The most common units for speed are metres per second (m/s), miles per hour (mph) and kilometres per hour (kph).
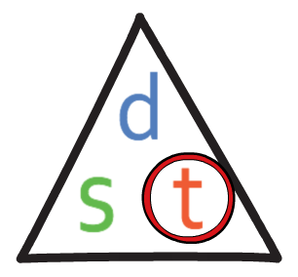
From the equation for working out speed, we can make the formula triangle below:
From the equation for working out speed, we can make the formula triangle below:
Whenever we are completing calculations to do with speed, distance and time, we need to make sure that the units are consistent.
Let’s have a few examples.
Let’s have a few examples.
Example 1
A runner jogs 200 m in 40 seconds. What is the runner’s average speed? Give your answer in metres per second.
We are able to work out the runner’s average speed by using the formula below:
A runner jogs 200 m in 40 seconds. What is the runner’s average speed? Give your answer in metres per second.
We are able to work out the runner’s average speed by using the formula below:
We are asked to work out the speed of our runner in metres per second (m/s). This means that the distance needs to be in metres and the time needs to be in seconds. We are told in the question that the distance is 200 m and the time is 40 seconds. The distance and time are in the units that they are meant to be in, which means that we can work out the speed by subbing the values into the formula:
The speed of the runner is 5 m/s.
Example 2
A cyclist is travelling at a speed 8 m/s. How long does it take for the cyclist to travel 432 metres?
The question is asking us to work out the time. We can use the formula triangle to find out the calculation that we need to undertake in order to work out the time taken. The formula triangle is shown below:
A cyclist is travelling at a speed 8 m/s. How long does it take for the cyclist to travel 432 metres?
The question is asking us to work out the time. We can use the formula triangle to find out the calculation that we need to undertake in order to work out the time taken. The formula triangle is shown below:
We are able to find out the calculation that we undertake by covering up the value that we are looking for. We are looking for the time, which means that we cover up t. This tells us that we need to complete the following calculation.
We are told in the question that the distance is 432 metres and the speed is 8 m/s. These units are consistent, which means that we can sub them into the formula.
Therefore, it takes the cyclists 54 seconds.
Example 3
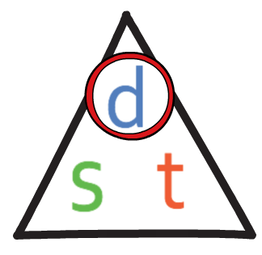
I am travelling on a motorway for 150 minutes at an average speed of 70 kph. How far do I travel during this time?
The question is asking us to work out the distance travelled by the car during this time. We can use the formula triangle to find out the calculation that we need to undertake in order to work out the distance travelled. The formula triangle is shown below:
I am travelling on a motorway for 150 minutes at an average speed of 70 kph. How far do I travel during this time?
The question is asking us to work out the distance travelled by the car during this time. We can use the formula triangle to find out the calculation that we need to undertake in order to work out the distance travelled. The formula triangle is shown below:
We are looking for the distance, which means that we cover up d on the above formula triangle. This tells us that we need to multiply the speed by the time.
We are given both the speed and time in the question; we are told that the speed is 70 kph and the time is 150 minutes. Currently, these units are not consistent. This is because the speed is given on kilometres per hour and the time is given in minutes. The easiest way to make the units consistent is to convert the minutes into hours. There are 60 minutes in an hour and this means that we can work out the time in hours by dividing 150 minutes by 60.
Therefore, the time is 2.5 hours. Our units are now consistent, which means that we are able to use the formula. The speed is 70 kph and the time is 2.5 hours. We sub these values into the formula:
The distance travelled is 175 km.