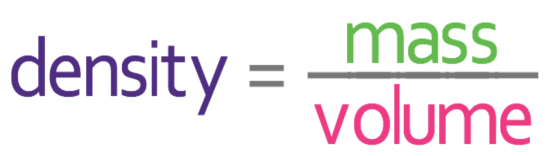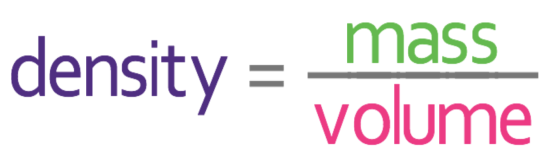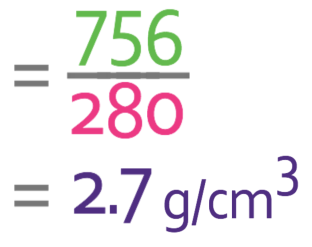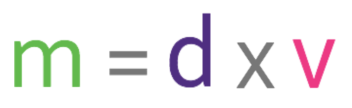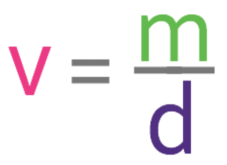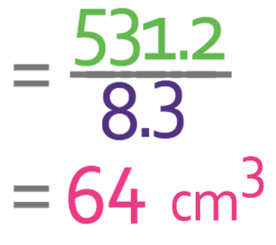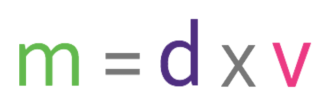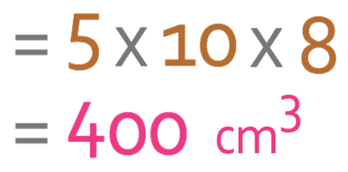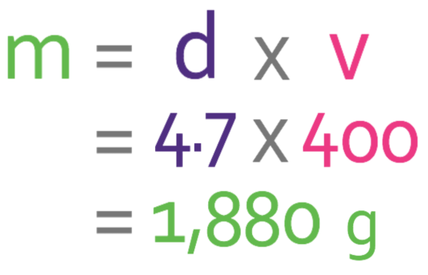4.10 K) Density
Density is a measure of how much mass is in a given volume; it essentially compares how heavy different substances are. We are able to work out density by using the following formula:
Density is usually measured in g/cm3 or kg/m3. When we are measuring mass in g/cm3, the mass is measure in grams and the volume is measured in cubic centimetres. When we are measuring mass in kg/m3, the mass is measure in kilograms and the volume is measured in cubic metres.
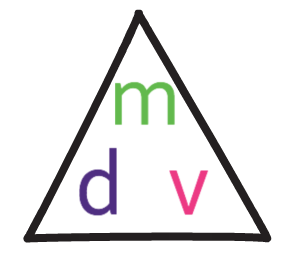
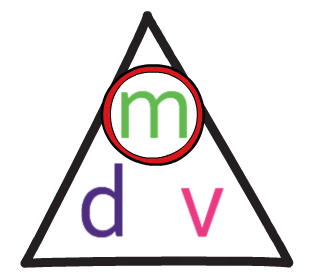
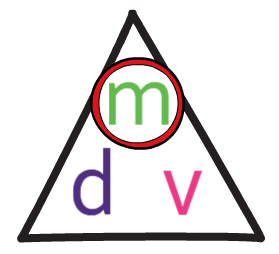
The formula triangle for density is shown below:
We use this formula triangle in the same way as all of the other formula triangles; we cover up what we are looking for to find the calculation that we need to undertake.
Let’s have a few examples.
A block of aluminium has a mass of 756g and a volume of 280 cm3. Work out the density of aluminium giving your answer is g/cm3.
We are able to work out the density by using the following formula:
We are asked to work out the density in g/cm3. In order to get this unit, we need to have the mass in grams and the volume in cm3. We are told that the mass of the aluminium is 756g and the volume is 280 cm3. These values are in the correct units, which means that we can sub these values into the formula.
The density of aluminium is 2.7 g/cm3.
A 2.8 m3 block has a density of 3,250 kg/m3. What is the mass of the block? Give your answer in kilograms.
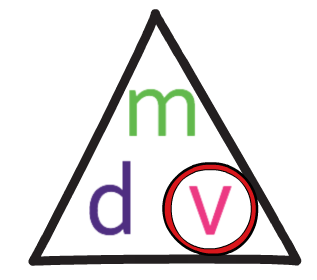
The question is asking us to work out the mass of the block. We are able to find the calculation that we need to undertake by using the density formula triangle. The formula triangle is shown below:
We are looking for the mass, so we cover up m in the formula triangle. This tells us that we need to undertake the following calculation:
The density has been measured in kg/m3 and the volume has been measured in m3. Both of these units are consistent, which means that we can sub the numbers from the question in the formula; we are told in the question that the density is 3,250 kg/m3 and the volume is 2.8 m3.
The mass of the block is 9,100 kg.
An object is made out a substance that has a density of 8.3 g/cm3. The mass of the object is 531.2 g. What is the volume of the object? Give your answer in cm3.
We find the calculation that we need to undertake by using the formula triangle.
We want to find the volume of the object, so we cover up v in the formula triangle. This tells us that we need to complete the following calculation.
We are told in the question that the mass of the object is 531.2 g and the density of the object is 8.3 g/cm3. Both of these units are consistent with one another, which means that we are able to sub them into the formula.
The volume of the cube is 64 cm3.
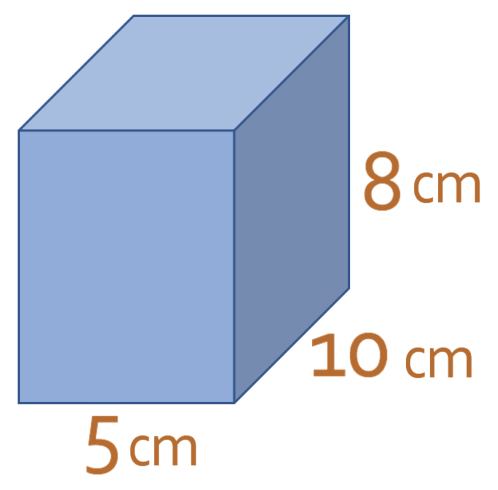
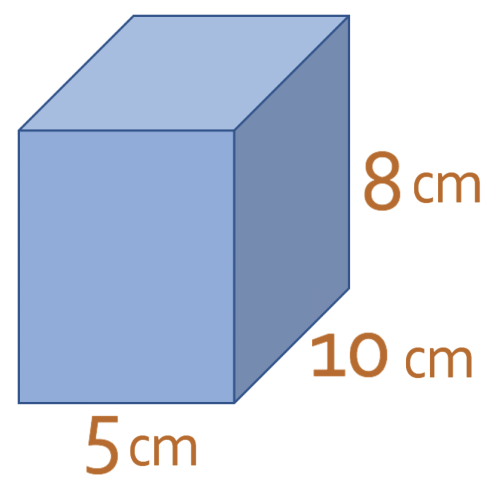
The cuboid below is made out of a material that has a density of 4.7 g/cm3. What is the mass of the cuboid? Give your answer in grams.
The question is asking us to work out the mass of the cuboid. We can use the formula triangle to see what calculation we need to undertake in order to work out the mass of the cuboid. The formula triangle is given below:
We are working out the mass, so we cover up m in the formula triangle. This tells us that we need to use undertake the calculation below:
The question tells us that the density of the material is 4.7 g/cm3. However, we are not told what the volume of the cuboid is. However, we are given the dimensions of the cuboid. A diagram of the cuboid is shown below.
We are able to work out the volume of the cuboid by multiplying the length by the width by the height. The formula is shown below:
We now sub the values that we are given from the cuboid diagram into the formula.
The volume of the cuboid is 400 cm3. We now have the volume of the cuboid and the density of the material that it is made out of; the density of the material is 4.7 g/cm3 and the volume is 400 cm3. We sub these values into the formula.
The mass of the cuboid is 1,880g.