Back to Edexcel Loci & Construction (F) Home
4.2 G) Bearings – Part 1
4.2 G) Bearings – Part 1
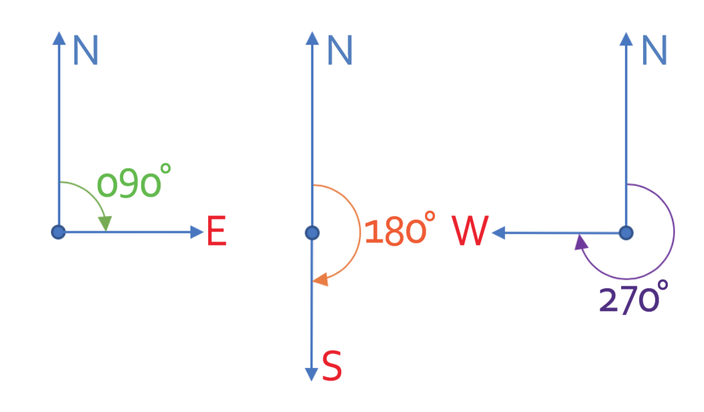
Bearings and compasses are used to give directions. There are four different main directions on a compass; north, south, east and west.
Ships use bearings for navigation. There are a few different rules that we need to remember when we are working with bearings. These rules are:
The bearing of east, south and west are shown below.
- They are measured from the North line
- They are measured in a clockwise direction
- They are measured in degrees and we always give them as 3 digits
The bearing of east, south and west are shown below.
Let’s have a few examples.
Finding Bearings
The first step in finding a bearing is to draw in a north line if there is not already a north line. If the bearing is less that 180°, we then measure the bearing clockwise from the north line (example 1). If the bearing is greater than 180°, we measure the angle anticlockwise and take the angle that we have measured off of 360° to give us the bearing (example 2).
The first step in finding a bearing is to draw in a north line if there is not already a north line. If the bearing is less that 180°, we then measure the bearing clockwise from the north line (example 1). If the bearing is greater than 180°, we measure the angle anticlockwise and take the angle that we have measured off of 360° to give us the bearing (example 2).
Example 1
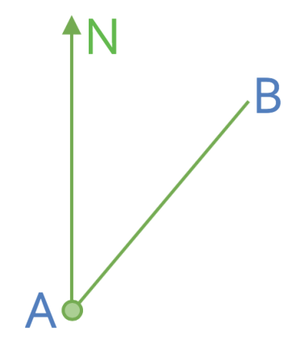
What is the bearing of B from A? The north line has been drawn for you. Click here for a printable version.
What is the bearing of B from A? The north line has been drawn for you. Click here for a printable version.
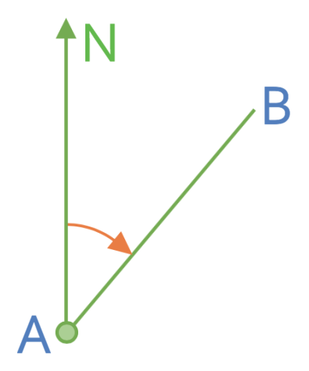
The word “from” in bearings is really useful as it tells us where we are measuring the bearing from. For this question, we are measuring the bearing from A. I have used an arrow to show what we are measuring on the diagram below.
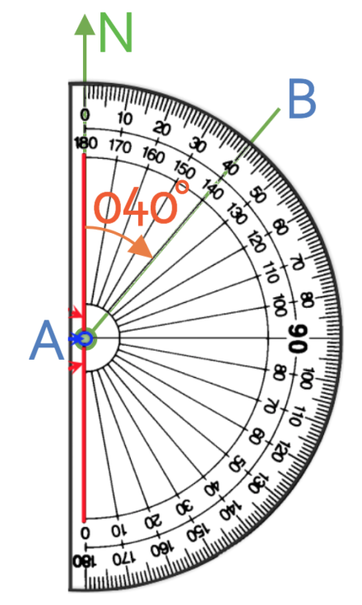
The bearing in the diagram below is less than 180°. Therefore, we are going to measure the angle that is between the north line and the bearing.
This angle is 40°. Therefore, the bearing is 040° (remember, we always need to give bearings as a 3-digit number, so we need to add a 0 at the front).
Example 2
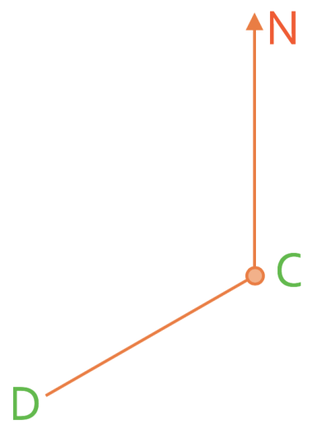
What is the bearing of D from C? The north line has been drawn for you.
What is the bearing of D from C? The north line has been drawn for you.
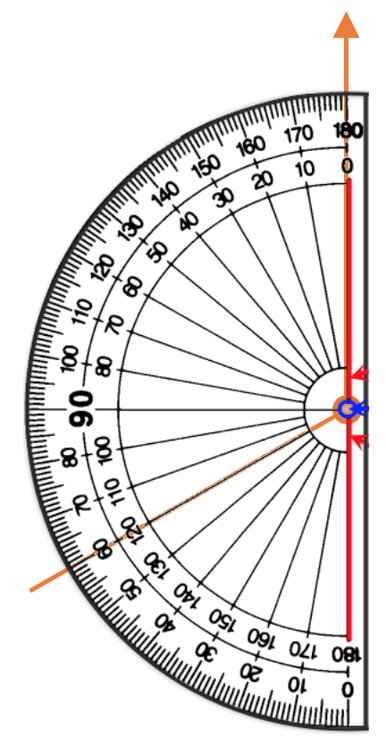
The bearing below is greater than 180°. Therefore, we are going to measure the angle between the north line and the bearing in an anticlockwise direction and then take this angle away from 360°.
The angle between the north line and the bearing is 120°. We take this off of 360°. The working is shown below:
The bearing of D from C is 240°.
Drawing the Bearing
Usually with a bearing question, you will be given the north line. However, if you are not given the north line, the first step will be to draw in a north line, which is a vertical line. The drawing of the bearing depends on whether the bearing is greater or less than 180°. If the bearing is less than 180°, we measure clockwise as normal (example 3). If the bearing is greater than 180°, we take the bearing away from 360° and measure this angle anticlockwise (example 4).
Usually with a bearing question, you will be given the north line. However, if you are not given the north line, the first step will be to draw in a north line, which is a vertical line. The drawing of the bearing depends on whether the bearing is greater or less than 180°. If the bearing is less than 180°, we measure clockwise as normal (example 3). If the bearing is greater than 180°, we take the bearing away from 360° and measure this angle anticlockwise (example 4).
Example 3
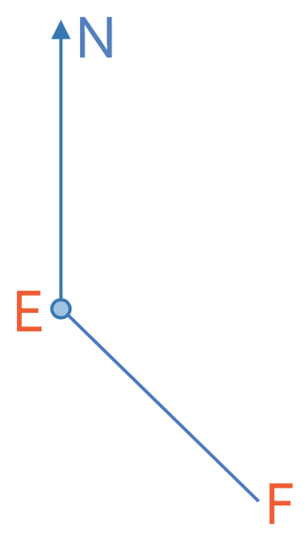
The bearing of F from E is 135°. Draw this bearing.
The bearing of F from E is 135°. Draw this bearing.
The north line has already been drawn for us. The angle for this bearing is 135°, which is less than 180°. Therefore, we measure the bearing in a clockwise direction. To measure out the angle, we place the centre of the protractor at E (the bottom of the north line) and measure 135° using the scale that starts from 0 at the north line. The working is shown below:
The final step is to draw a line from E to the mark that we have just made. The bearing is shown below:
Example 4
The bearing of H from G is 310°. Draw this bearing.
The bearing of H from G is 310°. Draw this bearing.
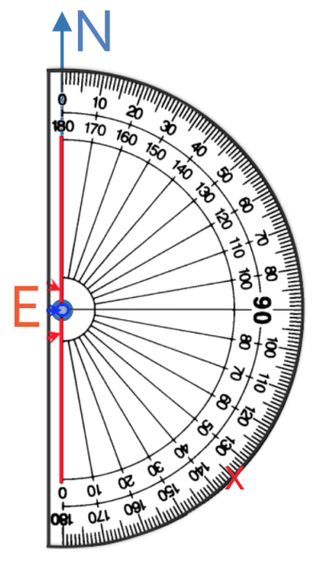
The north line has not been drawn for the question above. Therefore, the first step in answering this question is to draw in the north line, which is a vertical line.
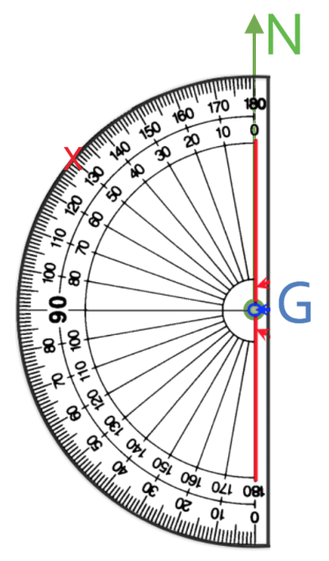
We are drawing the bearing of 310°, which is greater than 180°. Therefore, we take the bearing off of 360°.
We now measure 50° from the north line in an anticlockwise direction. The working is shown below:
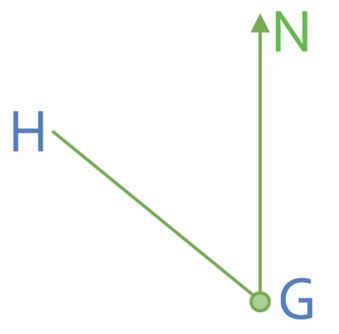
The final step is to draw a line from G to the mark that we have just made. The bearing is shown below: