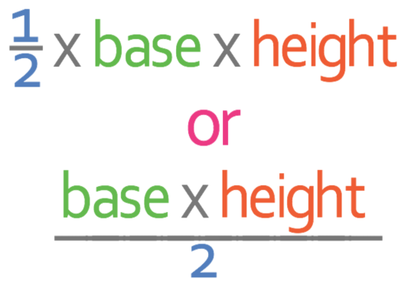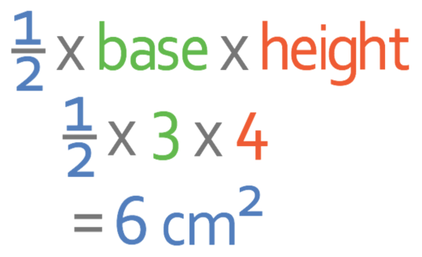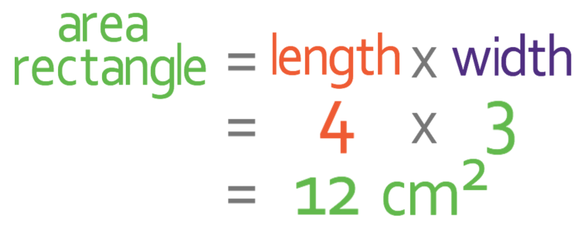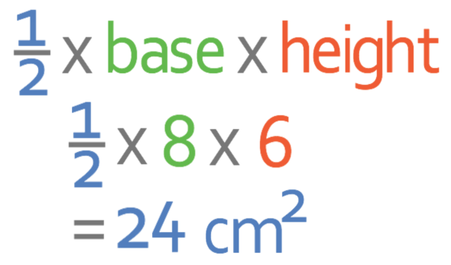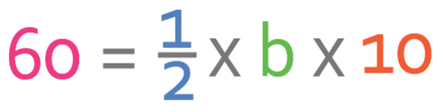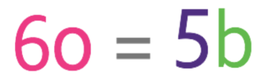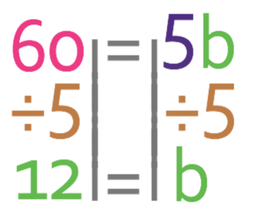Back to Edexcel 2D Shapes (F) Home
4.5 H) Area of Triangles – Part 1
The formula for working out the area of a triangle is:
​The triangle does not have to be a particular type of triangle for us to be able to use the above formula to work out the area of the triangle; all we need to know is the length of the base and the height of the triangle.
 
Sometimes in the exam, they will give you some sides of the triangle and you will need to find the height or base of the triangle by using Pythagoras’ theorem or maybe even trigonometry (we will be looking at these types of questions in the next section). Let’s start off with a fairly straight forward triangle.
Example 1
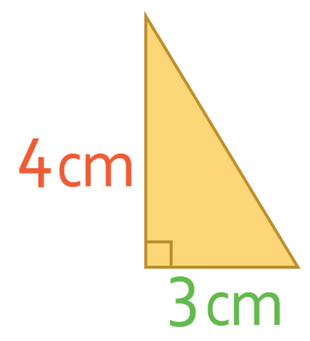
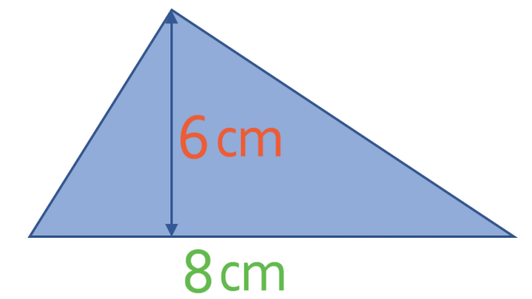
What is the area of the triangle below?
The base of the following right-angled triangle is 3 cm and the height of the triangle is 4 cm. Therefore, we sub these values into the generic formula for working out the area of a triangle. 

The area of this triangle is 6 cm2.

 

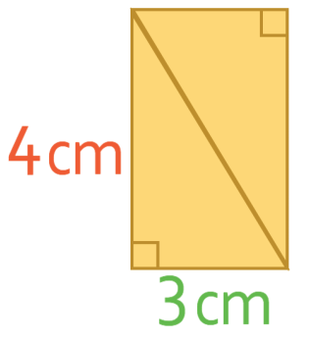
The above triangle is a right-angle triangle and I am now going to show how the formula comes about using this triangle. Let’s now turn the above triangle into a rectangle; the rectangle will have a length of 3 cm and a width of 4 cm.

From the section before, we learnt that we find the area of a rectangle by multiplying the length by the width. Therefore, the area of this rectangle is 12 cm2.

We can also see from the diagram that the area of the triangle is half the size of the area of the rectangle and this is where the half comes from in the formula. The base replaces the length in the area of a rectangle formula and the height replaces the width in the area of a rectangle formula.

Example 2 
What is the area of this triangle?
We are still going to be using the generic triangle formula to work out what the area of this triangle is. We are given the base and the height of the triangle. The base of the triangle is 8 cm and the height of the triangle is 6 cm. We can sub these values into the formula:

The area of the triangle is 24 cm2.

Example 3

It may be the case that you are given the area of a triangle and asked to work out what the length of the base or the height of the triangle is. We are able to answer questions like this by subbing in everything that we know into the area of a triangle formula. We then solve to find what is not known.

 

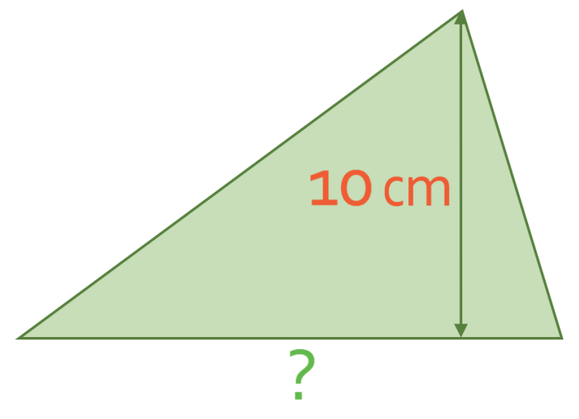
The area of the triangle below is 60 cm2. What is the length of the base of the triangle?

The formula for working out the area of a triangle is given below.

We are told in the question that the area of the triangle is 60 cm2. Also, we can see from the diagram that the height of the triangle is 10 cm. Let’s sub these values into the formula.

We can simplify the right side of the equation by multiplying ½ by 10, which gives us 5.

We want to find the value of b and not 5b. Therefore, we need to divide by 5 (we divide by the coefficient of the unknown).

This tells us that the base of the triangle is 12 cm.