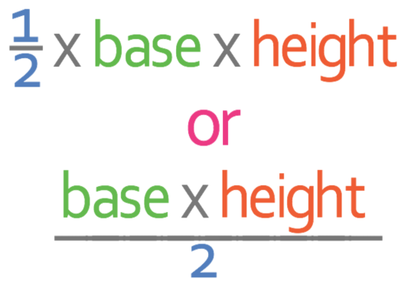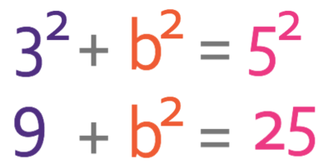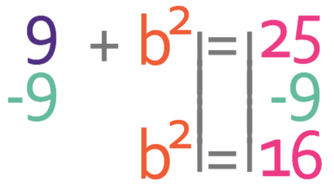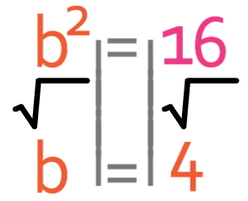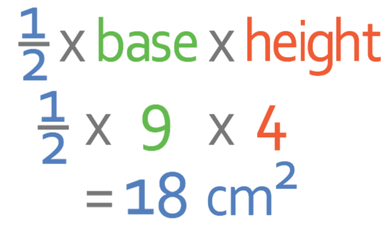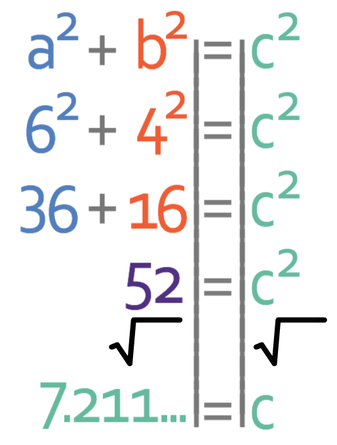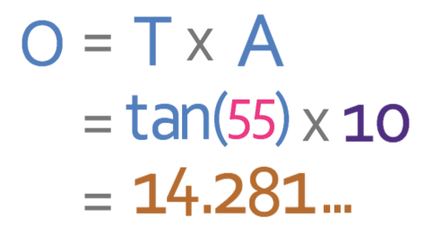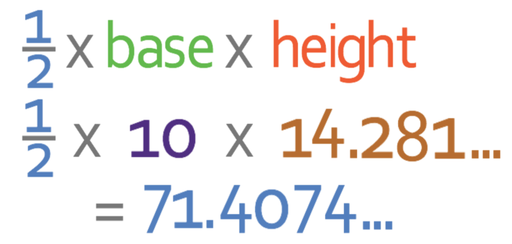Back to Edexcel 2D Shapes (F) Home
4.5 I) Area of Triangles – Part 2
We learnt in the previous section that the area of any triangle can be worked out by using either of the two formulas below:
​The examples in the section before were fairly straightforward. In this section, the examples are going to be more complex because they will require us to use Pythagoras’ theorem or trigonometry. If you are unsure about Pythagoras’ theorem and/or trigonometry, it is worth going through these sections before working through the next few examples (click here to be taken through to the Pythagoras’ theorem section and click here to be taken through to the trigonometry section).
Example 1 
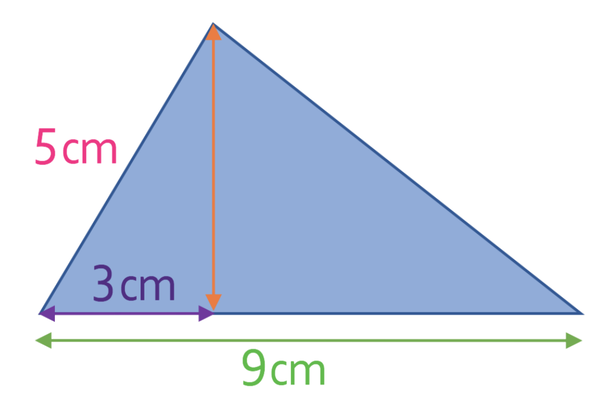
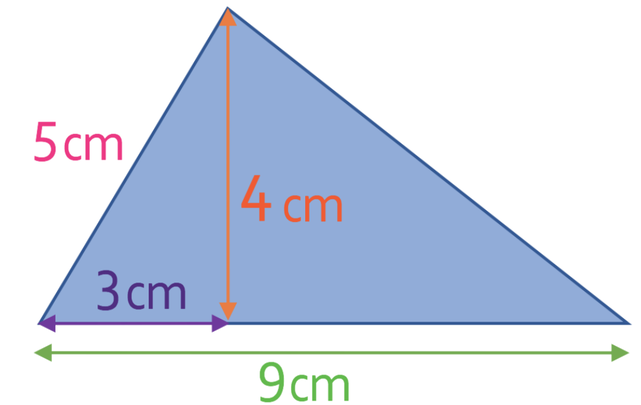
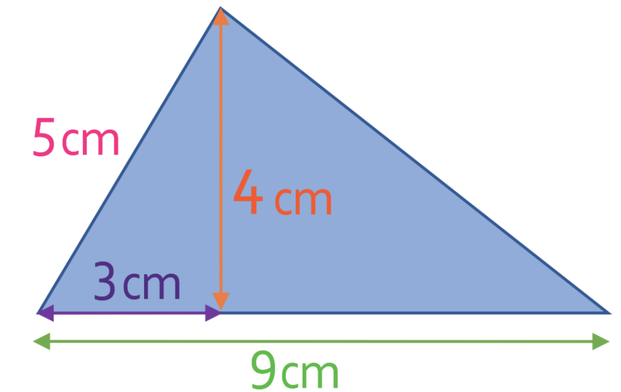
What is the area of the triangle below?
In order to use the triangle formula, we need to know what the base and the height of the triangle is. Currently we are given the base of the triangle, but we do not have the height of the triangle.
 
However, we are able to work out the height of the triangle by using Pythagoras’ theorem. The height of the triangle splits the whole triangle up into two smaller right-angle triangles. We are given the base and the hypotenuse for the right-angled triangle on the left. I have drawn this triangle out by itself so that it does not get confusing.  
I have labelled the hypotenuse as c, and the other two sides and a and b. We know the value of a and c; a is 3 and c is 5. We do not know the value of b and b is the height of this triangle. Pythagoras’ theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. His formula is given below:
We can now sub the values that we know into the formula. 

We now need to make b2 the subject and we do this by taking 9 from both sides.

The final step is to square root both sides and this is because we want to know what the value of b is rather than the value of b2.

The height of the right-angle triangle and the height whole triangle is 4 cm. Let’s add this value to our original diagram.

We are now able to work out the area of the whole triangle by subbing in 9 cm as the base and 4 cm as the height.

The area of the triangle is 18 cm2.

Extension

An extension for this question is to work out what the perimeter of the triangle is. The perimeter is the distance around the outside of the shape (give your answer to one decimal place).

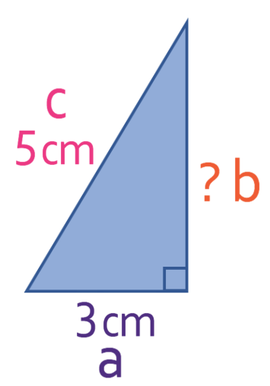
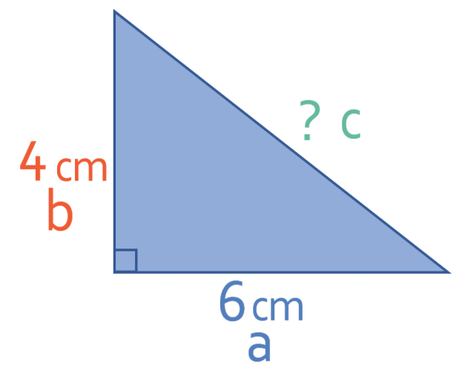
We have two of the three sides for our triangle; we do not have the downward sloping side on the right of the triangle. We are able to work the length of the other side by using Pythagoras’ theorem. When we used Pythagoras’ theorem, we used the right-angle triangle on the left. We are now going to use the right-angle triangle on the right to find out what the length of the downwards sloping side is.

 

Before we use Pythagoras’ theorem, we need to find out what the length of the base is for the right-angle triangle that is on the right. We know that the base of the whole triangle is 9 cm, and the base of the right-angle triangle on the left is 3 cm. This means that the base for the right-angle triangle on the right is 6 cm.

 

A sketch of the right-angle triangle on the right is given below.

We are looking for the hypotenuse of this triangle and we have the other two sides; the hypotenuse of the triangle in the formula is C. We can now sub the values that we have into the formula to see what the value of the hypotenuse is.

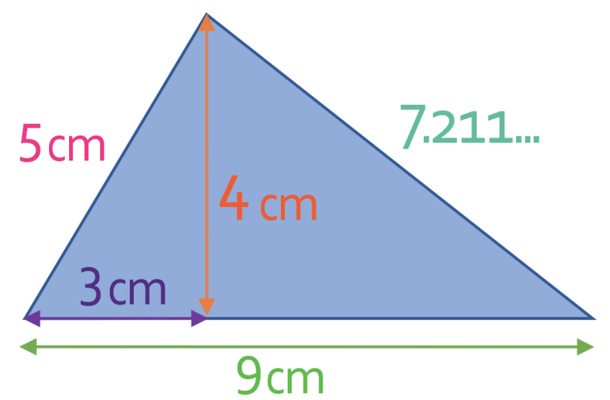
Let’s add this information to the diagram.

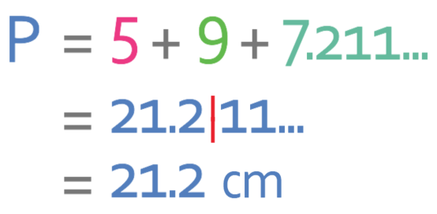
We are now able to work out the perimeter of this shape by adding up all of the outside lengths of the triangle.

The perimeter of the triangle is 21.2 cm.

Example 2

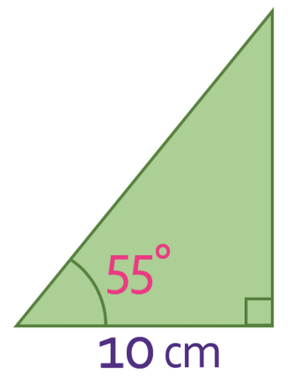
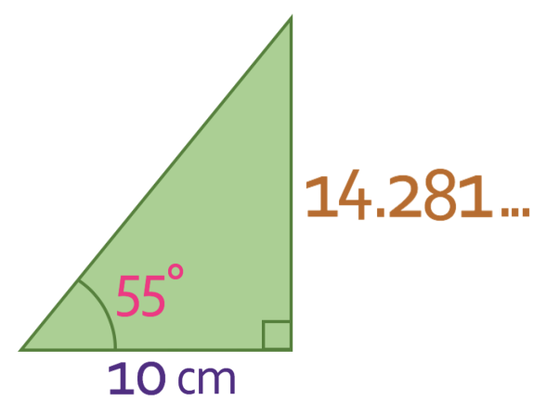
What is the area of the right-angled triangle below? Give your answer to two decimal places.

In order to work out the area of any triangle, we need to know what the base and the height of the triangle is. For the triangle above, we only have the base and do not yet have the height. However, this triangle is a right-angled triangle and we do have an angle in the triangle. This means that we are able to work out the height of the triangle by using trigonometry.

 

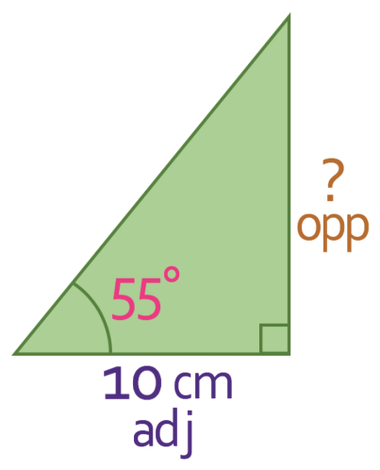
There are three different sides in triangles; hypotenuse, adjacent and opposite. The hypotenuse is always the longest side of the triangle; it does not matter what angle we are looking at. The opposite and the adjacent are dependent upon the angle that we are looking at. The adjacent is the side that is next to the angle that we are using, and it is the side that is not the hypotenuse. The opposite is the side that is opposite the angle that we are looking at.

 

In the triangle that we are given, we have an angle and the adjacent and we want to find the opposite. The labelled triangle is shown below:

We now need to find out which trigonometry formula triangle we will be using. The trigonometry formula triangles are given below:

We are going to be using the TOA trigonometry formula triangle. When using formula triangles (for maths or science), we cover up what we are looking for and do the operation that is left. We are looking for the opposite, which means that we cover up the opposite.

When we do this, we see that the operation that we need to undertake is:

We are now able to sub the values in.

We can add this information to our diagram.

We now have the height of our triangle, which means that we are now able to find the area of the triangle.

We are asked in the question to give our answer to two decimal places.

The area of the triangle is 71.41 cm2.