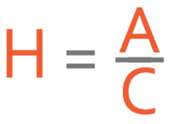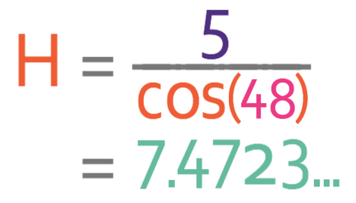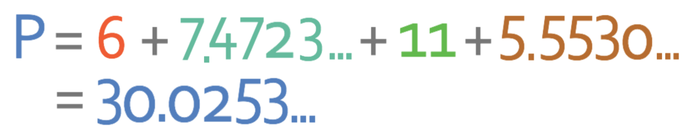Back to Edexcel 2D Shapes (F) Home
4.5 M) Perimeter of Trapeziums
4.5 M) Perimeter of Trapeziums
The perimeter of a 2D shape is the total distance around the outside of the shape. In this section we are going to be looking at working out the perimeter of a trapezium.
Example 1
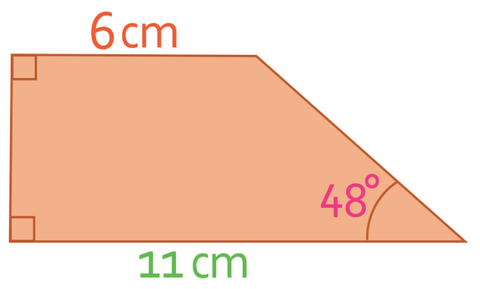
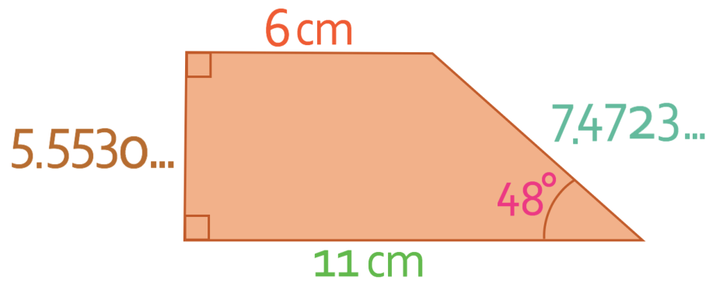
What is the perimeter of the trapezium below? Give your answer to two decimal places.
What is the perimeter of the trapezium below? Give your answer to two decimal places.
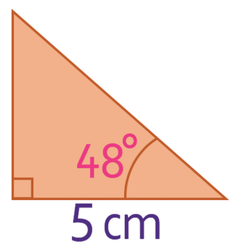
In order to work out the perimeter of a trapezium, we need to know the lengths of all of the sides of the trapezium. For the trapezium above, we have the length of two of the sides and we do not know what the lengths are for the other two sides. Therefore, we need to find the length of these two sides before we are able to work out the perimeter. We are going to find these two lengths by creating a right-angle triangle on the right of the trapezium. The base of this right-angle triangle will be the difference between length of the top and the bottom of the trapezium; this means that the length of the base of the triangle is 5 cm (11 – 6).
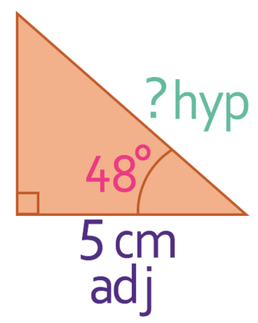
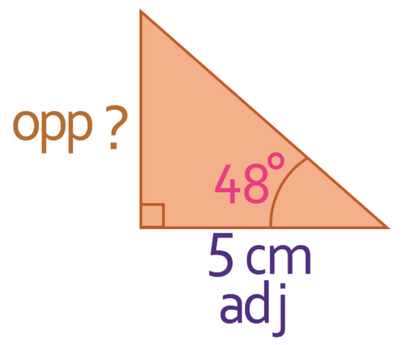
We are now able to work out the length of the slanted side. The slanted side is the hypotenuse of the right-angled triangle and the base (the side that is 5 cm) is the adjacent. The labelled triangle is shown below.
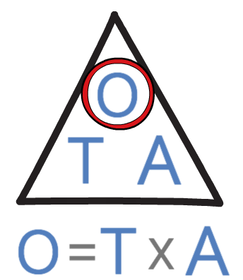
The trigonometry formula triangles are shown below.
We are looking for the trigonometry triangle that contains an angle, the adjacent and the hypotenuse. This means that we are going to be using the CAH formula triangle.
We are looking for the hypotenuse, so we cover up H in the above formula triangle to see the operation that we need to undertake. The operation that we need to undertake is given below:
The next step is to sub the values that we are given into the formula:
The length of the slanted side is 7.4723… cm. As this is not our final answer, it is best to keep quite a few decimal places in our working.
We now need to find the length of the side that is on the left. This side is going to be the same length as the perpendicular height of the trapezium. We are able to find the perpendicular height of the trapezium from the same right-angled triangle that we used earlier. The right-angle triangle is shown below.
We now need to find the length of the side that is on the left. This side is going to be the same length as the perpendicular height of the trapezium. We are able to find the perpendicular height of the trapezium from the same right-angled triangle that we used earlier. The right-angle triangle is shown below.
We are looking for the opposite on the right-angle triangle. Also, we have the adjacent for the right-angled triangle. Therefore, we are going to be using the trigonometry formula triangle that contains an angle, the adjacent and the opposite.
This means that we are going to be using the TOA formula triangle. We are looking for the opposite, which means that we will be completing the following calculation.
The next step is to sub the values in.
The perpendicular height and the length of the side of the left is 5.5530… cm.
We now have the lengths of all of the sides of the trapezium.
We now have the lengths of all of the sides of the trapezium.
We work out the perimeter of the trapezium by adding all of the lengths together.
The question asks us to give our answer to two decimal places.
The perimeter of the trapezium is 30.03 cm.