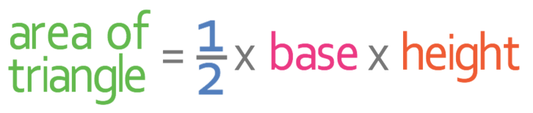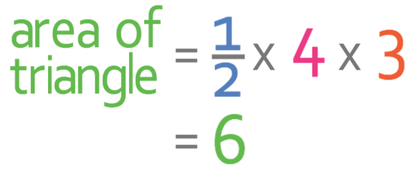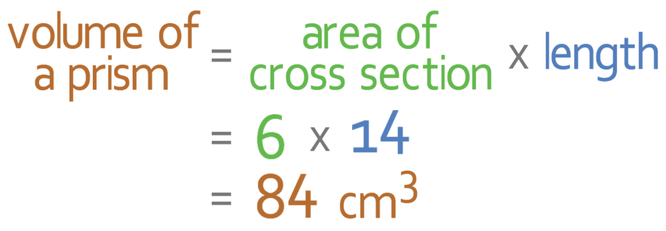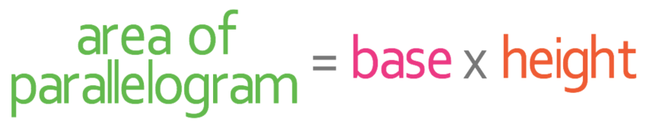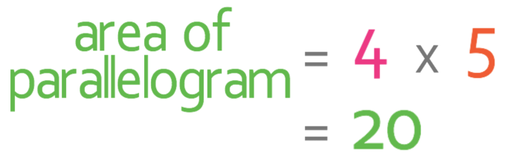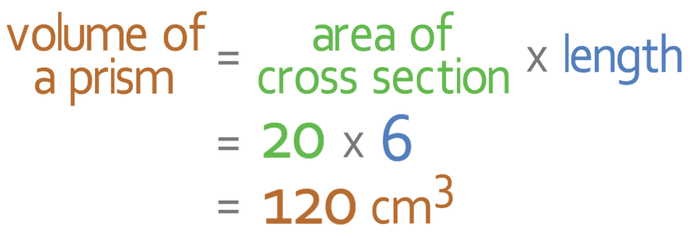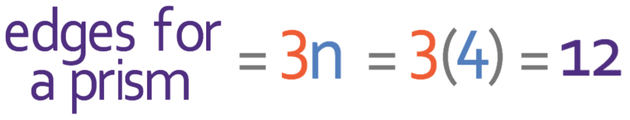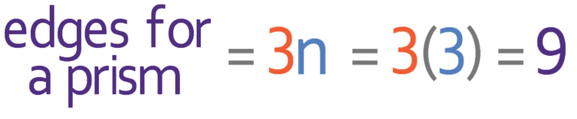Back to Edexcel 3D Shapes (F) Home
4.6 D) Prisms
4.6 D) Prisms
A prism is a solid shape that has identical ends, flat faces and the same cross section along its length (if you were to cut a prism into slices along its length, the cross sections will be always be the same; the cross sections will be the same size as the identical ends). An example is a Toblerone box.
We are able to work out the volume of a prism by multiplying the area of the cross section by the length of the prism.
Let’s have a few examples.
Example 1
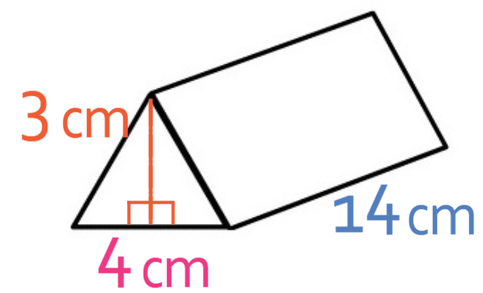
What is the volume of the prism below?
What is the volume of the prism below?
We work out the volume of a prism by using the following formula.
At the moment, we do not know what the area of the cross section is. The prism is a triangular prism, and the cross section is a triangle. The formula for working out the area for a triangle is:
The base of our triangle is 4 and the height is 3. We can sub these values into our formula to find the area of the cross section.
We are now able to find the volume of our prism because we know that the area of the cross section is 6 and the length of the prism is 14.
Therefore, the volume of the prism is 84 cm3.
Example 2
Sometimes in the exam, you will be given a diagram of the cross section of a prism, told the length of the prism and then asked to work out the volume of the prism. Example 2 is a question like this.
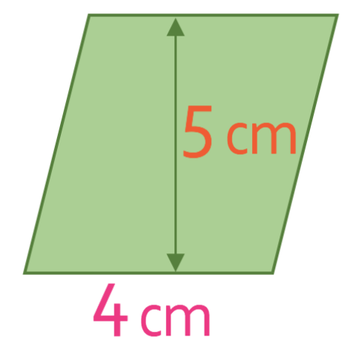
The cross section of a prism is a parallelogram and a diagram for the cross section is shown below.
Sometimes in the exam, you will be given a diagram of the cross section of a prism, told the length of the prism and then asked to work out the volume of the prism. Example 2 is a question like this.
The cross section of a prism is a parallelogram and a diagram for the cross section is shown below.
The prism has a length of 6 cm. What is the volume of the prism?
In order to work out the volume of the prism, we need to know what the area of the cross section is. The cross section on this prism is a parallelogram and from the 2D shape section, we know that the formula for working out the area of a parallelogram is:
In order to work out the volume of the prism, we need to know what the area of the cross section is. The cross section on this prism is a parallelogram and from the 2D shape section, we know that the formula for working out the area of a parallelogram is:
Feel free to go through the area of a parallelogram section before continuing this question if the above formula looks unfamiliar (click here to be taken to the parallelogram section).
The base of the parallelogram is 4 and the height is 5. We can sub these values into the formula:
The base of the parallelogram is 4 and the height is 5. We can sub these values into the formula:
The next step is to multiply the area of the cross section by the length of the prism, which is 6.
The area of this prism is 120 cm3.
Number of Edges for Prisms
The number of edges that a prism has will be three times the number of sides that the cross section has. If the number of sides that the cross section of a prism has is n, the number of edges that the prism has will be 3n.
The number of edges that a prism has will be three times the number of sides that the cross section has. If the number of sides that the cross section of a prism has is n, the number of edges that the prism has will be 3n.
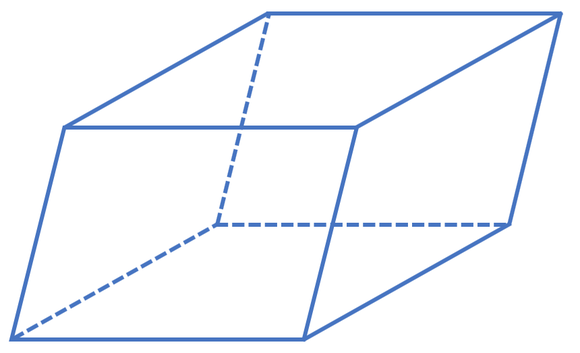
For example, let’s find the number of edges that the prism below has. The cross section of the prism below is a parallelogram.
The number of sides that the cross section has is 4 (n is 4). We can work out the number of edges that this prism has by subbing n as 4 into the formula for working out the number of edges that a prism has (3n). The working is shown below:
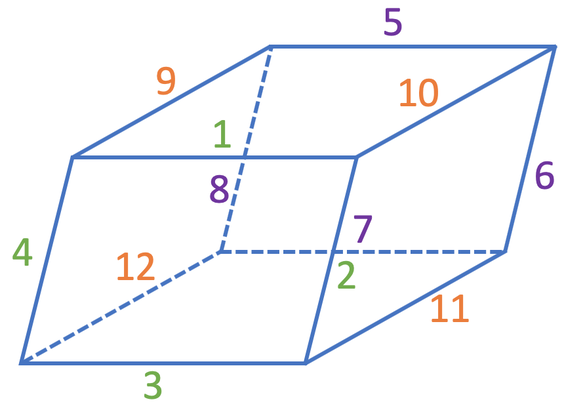
This tells us that the prism above will have 12 edges. From looking at the diagram of the prism, we can see that this prism does have 12 edges because the prism will have 4 edges on the cross section nearest us, 4 edges of the cross section furthest away from us and 4 edges that join the two cross sections together; all of these edges make 12 edges.
The 3 in the formula for working out the number of edges that a prism has (3n) comes from one cross section (1 – green), the other cross section (2 - purple) and the edges that join the two cross sections together (3 – orange).
Triangular prism
Let’s now have a look at a triangular prism and work out the number of edges that it has. A diagram of a triangular prism is shown below.
Triangular prism
Let’s now have a look at a triangular prism and work out the number of edges that it has. A diagram of a triangular prism is shown below.
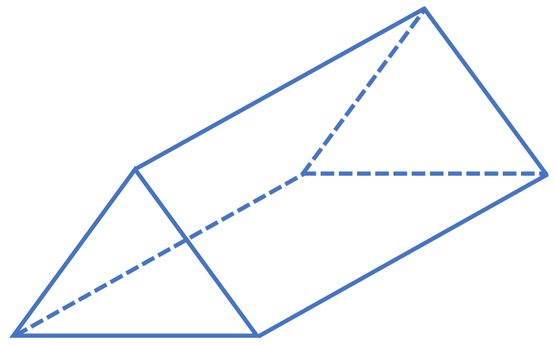
The cross section of the prism is a triangle and the cross section has 3 sides (n is 3). We can work out the number of edges that the prism has by subbing n as 3 into the formula for working out the number of edges that a prism has (3n). The working is shown below:
This tells us that a triangular prism will have 9 edges.
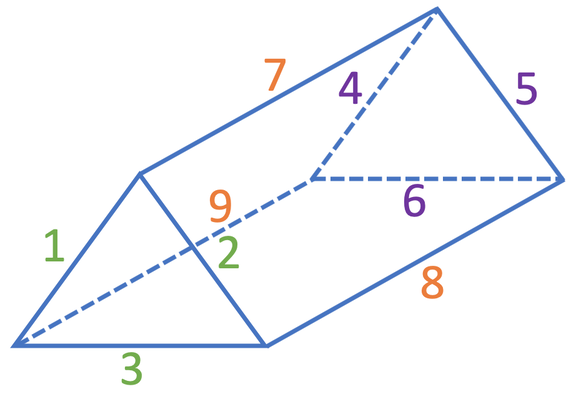
We can use the diagram of the triangular prism to check that the prism does have 9 edges. There are 3 edges on the cross section nearest us (green), 3 edges on the cross section furthest away from us (purple) and 3 edges that join the two cross sections together (orange); all of these edges make a total of 9 edges.
We can use the diagram of the triangular prism to check that the prism does have 9 edges. There are 3 edges on the cross section nearest us (green), 3 edges on the cross section furthest away from us (purple) and 3 edges that join the two cross sections together (orange); all of these edges make a total of 9 edges.
The rule for the number of edges that a prism has is a little bit tricky to remember. Therefore, it is worth getting the rule and an example down on a revision card.