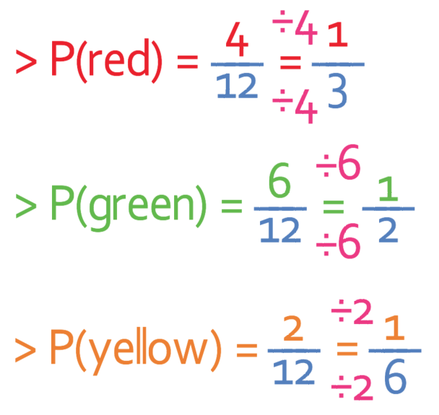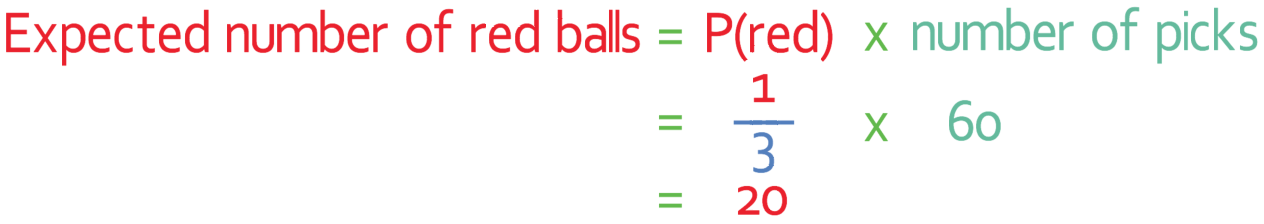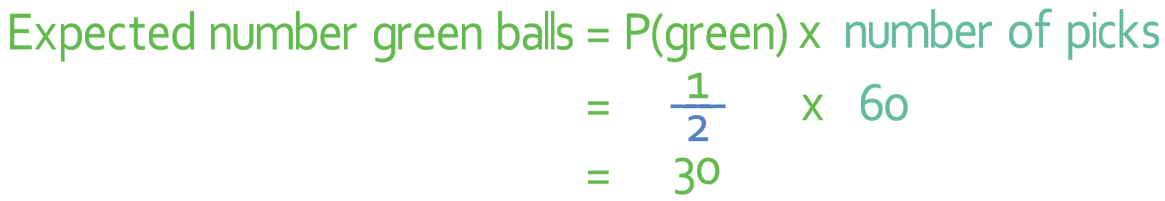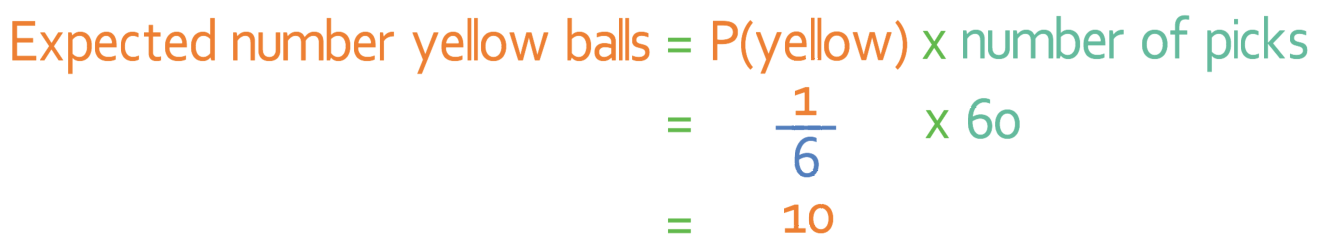Back to Probability Foundation Home
5 F) Predicting Outcomes – Part 2
5 F) Predicting Outcomes – Part 2
The content in this section builds on the content that was looked at in the section before. Make sure that you have gone through the content in the previous section before working through this section (click here to be taken through to the previous section).
Example 1
We have a bag that contain 12 balls that are 3 different colours. The 3 different colours are red, green and yellow. The bag contains 6 green balls and 2 yellow balls. We are going to pick a ball out of the bag and replace the ball 60 times (we are going to note the colour of the ball and then place the ball back into the bag).
1) What is the probability of picking each of the different colours? Give your answers as a fraction.
2) What is the expected number of times that we will pick each of the three colours out of the bag?
The question gives the number of green and yellow balls, but not the number of red balls. We know that there are 12 balls in the bag and we can rearrange the equation and sub in the respective values to find the number of red balls that are in the bag.
We have a bag that contain 12 balls that are 3 different colours. The 3 different colours are red, green and yellow. The bag contains 6 green balls and 2 yellow balls. We are going to pick a ball out of the bag and replace the ball 60 times (we are going to note the colour of the ball and then place the ball back into the bag).
1) What is the probability of picking each of the different colours? Give your answers as a fraction.
2) What is the expected number of times that we will pick each of the three colours out of the bag?
The question gives the number of green and yellow balls, but not the number of red balls. We know that there are 12 balls in the bag and we can rearrange the equation and sub in the respective values to find the number of red balls that are in the bag.
We can rearrange the equation to make red balls the subject and then find the number of red balls.
We now know how many balls of each colour there are in the bag; there are 4 red balls, 6 green balls and 2 yellow balls. From this information, we can work out the probability of picking a particular coloured ball. We work out the probability of a particular coloured ball by using the following formula:
When we use this equation, we see that the probability of the colours are as follows (we need to remember to simplify the probabilities if we are giving them as fractions):
These probabilities are will be the same for every time that we pick a ball out of the bag. This is because we are picking a ball out, noting the colour and then replacing the ball in the bag. By replacing the ball that we have picked, the total number of balls and the number of each colour ball in the bag remains constant. This means that the probabilities of picking each of the coloured balls remains constant.
We are now able to work out the expected number of times that a particular coloured ball will be picked by multiplying the probability of a particular colour by the number of times that we pick a ball out of the bag (which is 60).
Let’s first work out the expected number of times that we will pick a red ball.
We are now able to work out the expected number of times that a particular coloured ball will be picked by multiplying the probability of a particular colour by the number of times that we pick a ball out of the bag (which is 60).
Let’s first work out the expected number of times that we will pick a red ball.
The expected number of times that a red ball will be picked is 20.
Let’s do the same process but for green balls.
Let’s do the same process but for green balls.
And finally, let’s find the expected number of times that a yellow ball will be picked.
Therefore, if we were to pick a ball out 60 times and replace the ball, we would expect to pick a red ball 20 times, a green ball 30 times and a yellow ball 10 times.