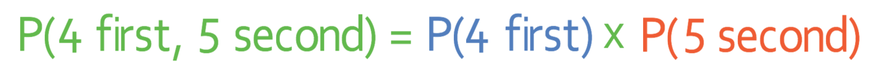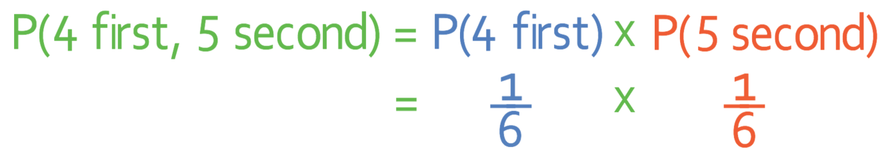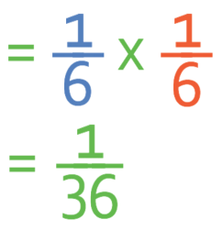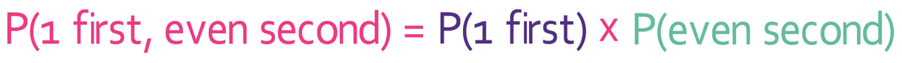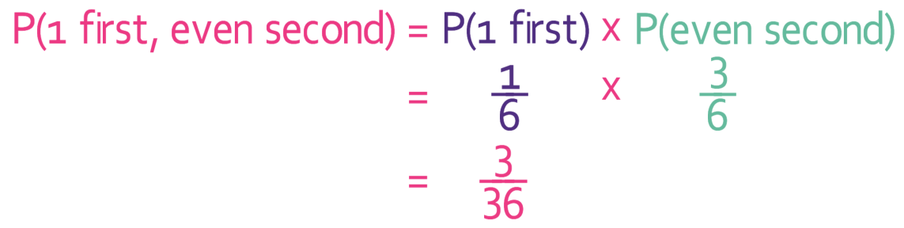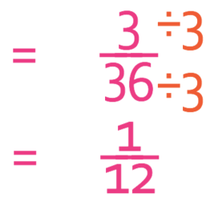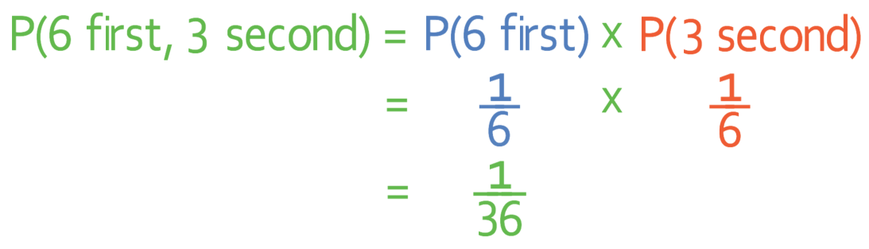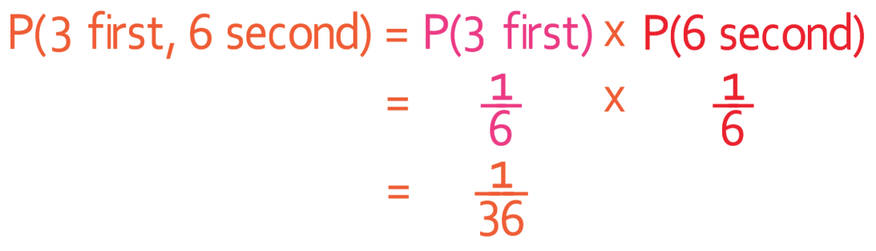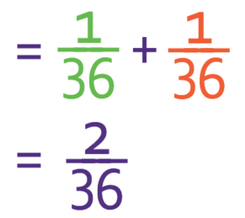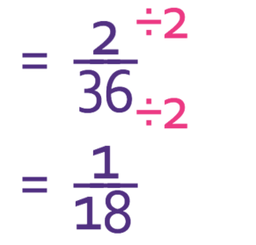Back to Edexcel Probability (F) Home
​​5 J) Combined Events – Probabilities: Part 1
In the section before we looked at finding the number of different possible outcomes when we have two or more events occurring. In this section, we are going to be looking at finding the probabilities of a combination of different events happening. In order to find the probability of a combination of different events happening, we multiply the probabilities of each of the individual events happening together. 
Example 1
I am going to roll a fair dice two times.
a) What is the probability of rolling a 4 on the first roll and then a 5 on the second roll?
b) What is the probability of rolling a 1 on the first roll and an even number on the second roll?
c) What is the probability of rolling a 6 and a 3 in any order?
 
Part a
We can find the probability of rolling a 4 on the first roll and a 5 on the second roll by multiplying the probabilities of each of these events together. 

The probability of rolling a 4 on the first roll is 1/6 and the probability of rolling a 5 on the second roll is also 1/6. Therefore, the calculation becomes:

When we are multiplying fraction, we multiply straight across; we multiply the numerators to obtain the numerator in the answer, and we multiply the denominators to obtain the denominator in the answer.

The final step is to check whether our fraction can be simplified. There are no common factors between 1 and 36, which means that our fraction is in its simplest form.

 

Part b

We find the probability of rolling a 1 and an even number by multiplying the probabilities of these separate events occurring.

The probability of rolling a 1 is 1/6. There are 3 even numbers on a dice (2, 4 and 6). Therefore, the probability of rolling an even number is 3/6 (or ½). Let’s now sub these into the equation above and complete the calculation.

The final step is to check whether the fraction can be simplified. There is a common factor of 3 between the numerator and the denominator. Therefore, we divide the numerator and the denominator by 3.

Part c

Part c asks us to work out the probability of rolling a 6 and a 3 in any order. We need to be really careful with questions like this and this is because there are two different ways that we are able to obtain a 6 and a 3.

1) We roll a 6 on the first roll and a 3 on the second roll

2) We roll a 3 on the first roll and a 6 on the second roll

 

As there are two different ways that we can obtain a 6 and a 3, we need to find the probability of each of these ways seperately and then add the probabilities together.

 

Let’s first find the probability of obtaining a 6 on the first roll and a 3 on the second roll.

We are now going to do the same for a 3 on the first roll and a 6 on the second roll.

The next step is to add the two different probabilities together.

When we are adding fraction, we need to make sure that the denominators of the fractions are the same. When the denominators are the same, we add the numerator to obtain the numerator in the answer and keep the denominator in the answer the same.

 

The denominators for both of the above fractions are 36. Therefore, we are able to add the fractions.

The final step is to simplify. The numerator and the denominator both have a factor of 2. Therefore, we can divide the numerator and the denominator of the fraction by 2.

Therefore, the probability of picking a 6 and a 3 in any order is 1/18.