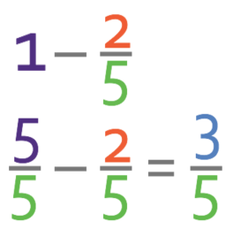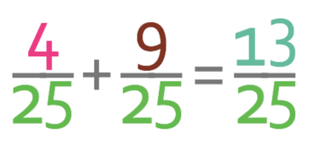Back to Edexcel Probability (F) Home
​5 P) Probability Trees – Part 2
​In the previous section, I mentioned that the probabilities on the branches coming from the same point must add up to 1. This is an essential rule to remember because sometimes you will have a probability tree with some probabilities given and other probabilities left out. From the rule and the probabilities that you are given, you will be able to work out the missing probabilities. This is going to be the case in example 1. 

Example 1

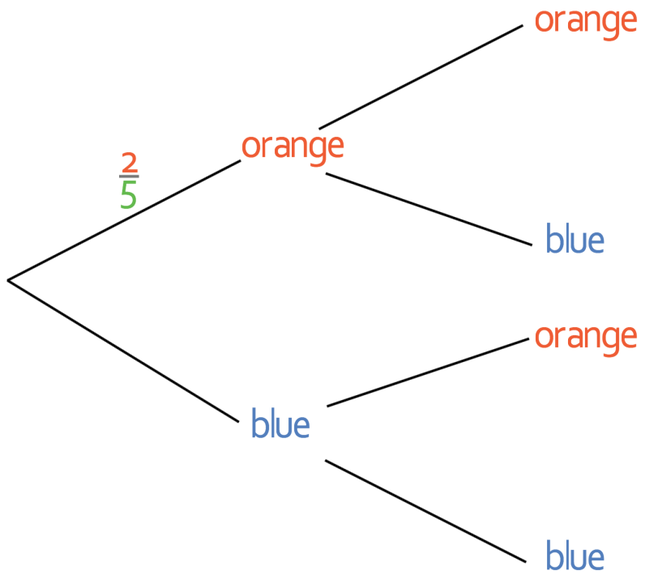
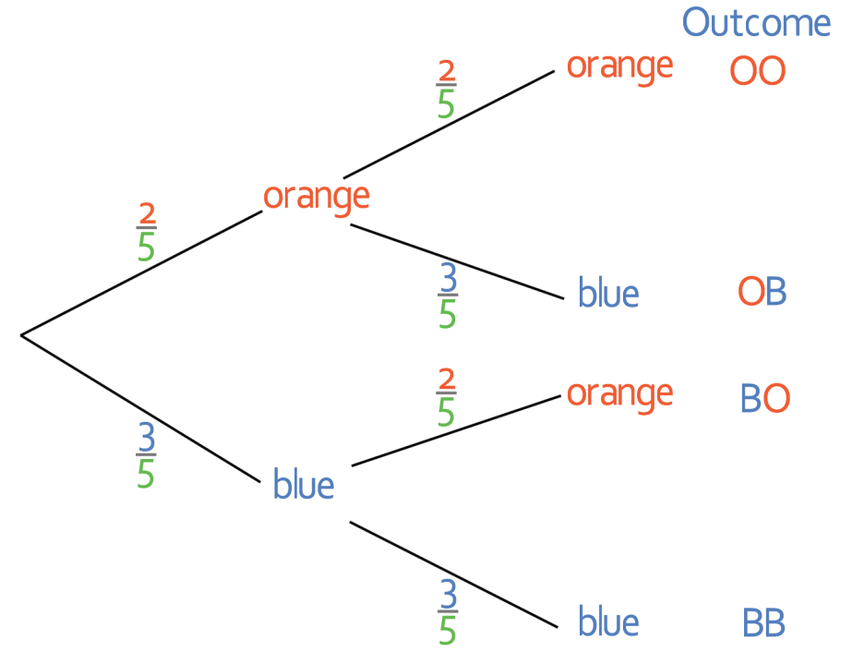
A bag contains orange and blue balls. A ball is picked out of the bag twice and replaced after each pick. There is a partially completed probability tree below.

a) Complete the probability tree

b) Find the probability of picking balls of the same colour

 

Part a

Part a in the question asks us to fill in the probability tree. We are only given one of the probabilities on the probability tree and this is the probability of picking an orange ball on the first pick (probability is 2/5). From this information, we are able to work out the probability of picking a blue ball on the first pick. We are able to do this because we know that the probabilities on the branches from the same point must add up to 1. Therefore, the probability of picking an orange ball on the first pick and picking a blue ball on the first pick must add up to 1. Therefore, we can find the probability of picking a blue ball on the first pick by doing the following calculation.

Therefore, the probability of picking a blue ball on the first pick is 3/5.

 

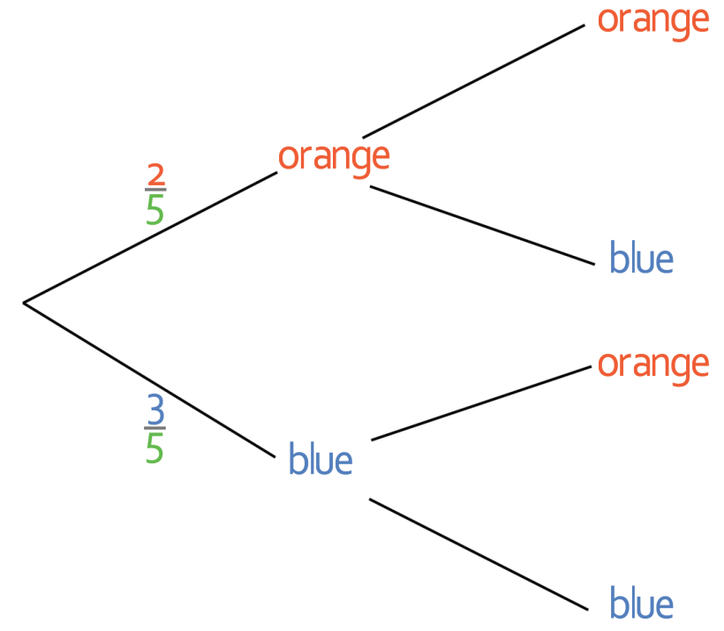
We are told in the question that the ball is picked out of the bag and then replaced and this means that the probabilities of picking each of the colours is constant; the probability of picking an orange ball will always be 2/5 and the probability of picking a blue ball will always be 3/5. We can place these probabilities onto the tree.

Part b

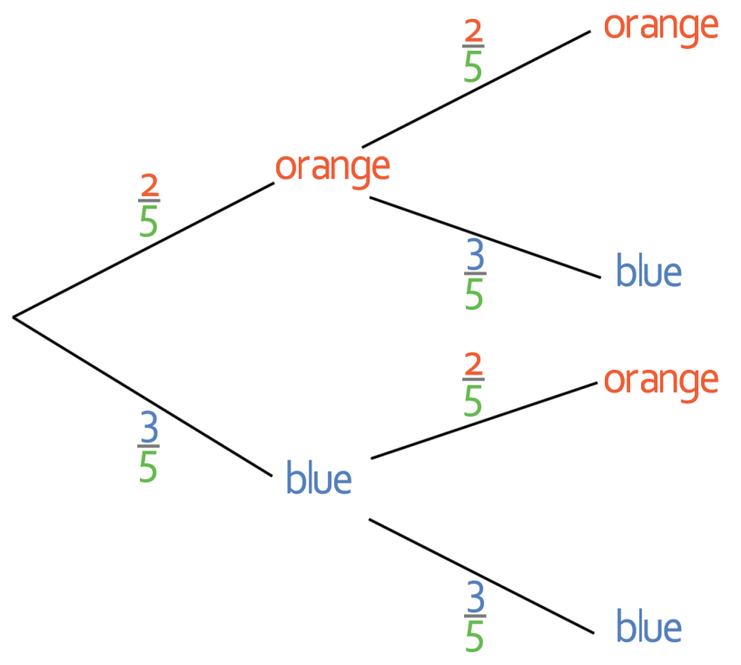
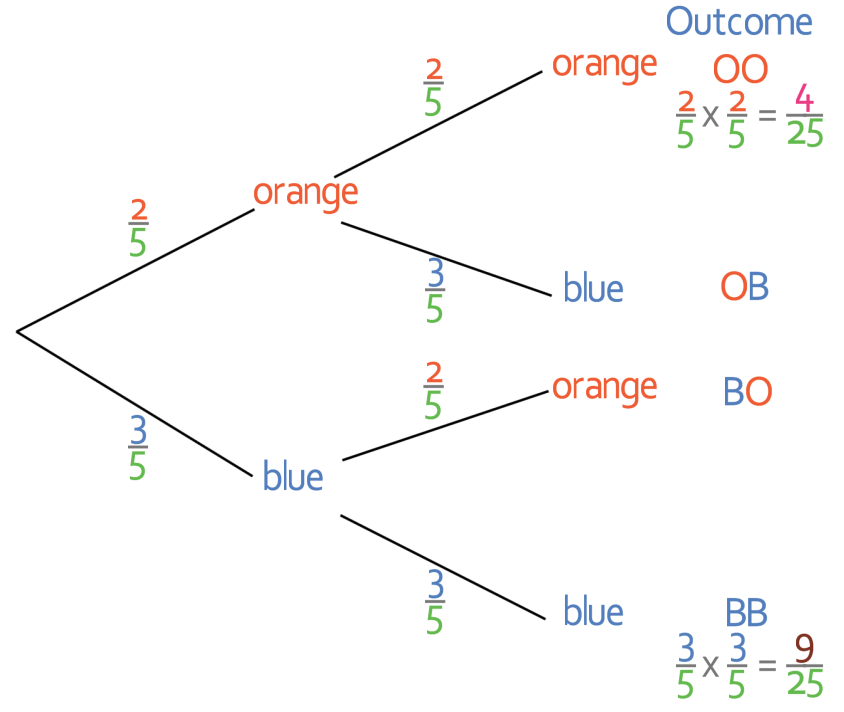
Part b asks us to find the probability of a certain event taking place. Before we start answering any questions like this, I think that it is a good to list the outcomes at the end of the branches. We find the outcomes by following the branches on the probability trees. The outcomes are shown on the probability tree below.

We are asked to find the probability of picking two balls of the same colour. From the outcomes column we can see that there are two different outcomes where the balls are the same colour; the balls can either be both orange (first outcome) or both blue (bottom outcome). In order to find the probability of these outcome occurring, we multiply the probabilities on the branches to get to that outcomes.

The final step is to add the probabilities of each of these events happening together. The calculation is shown below.

Therefore, the probability of picking two balls of the same colour is 13/25.