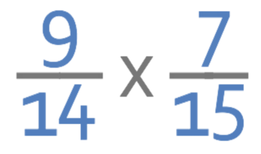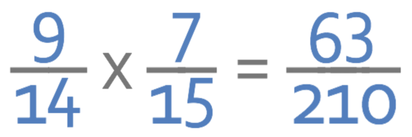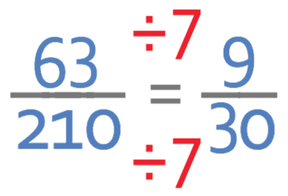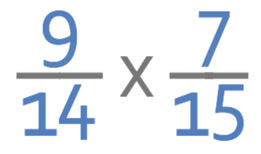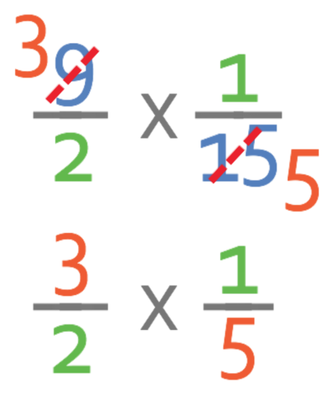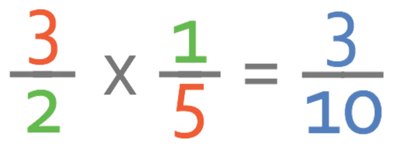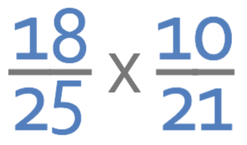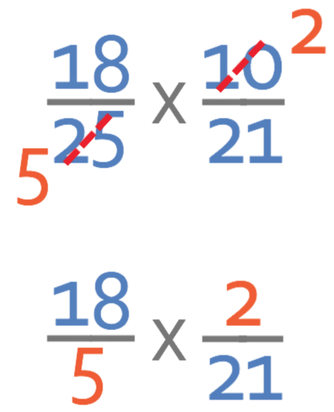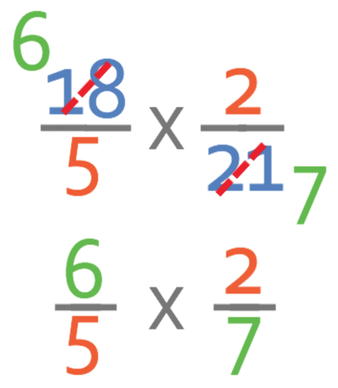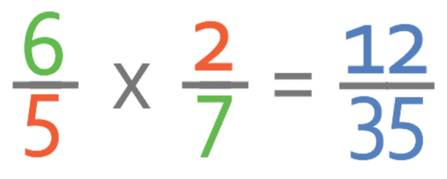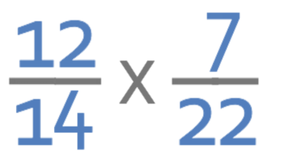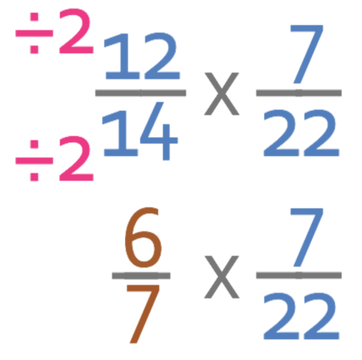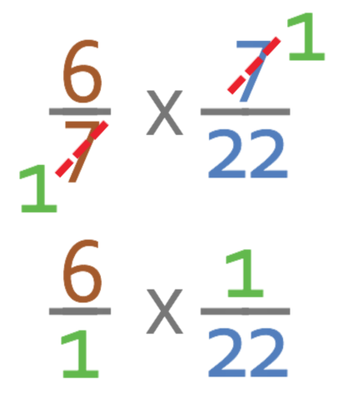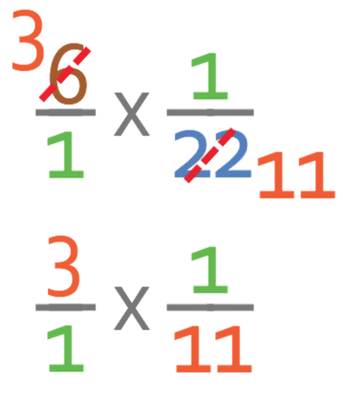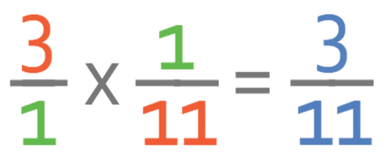1.3 L) Multiplying Fractions – Part 3
In this section we are going to be multiplying fractions without a calculator where the numbers involved in the fractions are quite large. There are two different ways that we can answer these types of questions:
- One way is to multiply the fractions in the same way as before.
- The second method is to simplify/ cancel the fractions by common factors between all of the numerators and all of the denominators (this will make more sense after we have looked at the examples in this section).
The second method is considerably easier than the first method when the numbers in the fractions are quite large. Let’s have an example that I will answer using both methods.
Do not use a calculator to answer this question.
Complete the calculation below. Give your answer as a fraction in its simplest form.
The first method involves multiplying the fractions in the usual way; we multiply the numerators of the fractions to obtain the numerator in the answer, and we multiply the denominators of the fractions to obtain the denominator in the answer.
For the numerators, we are multiplying 9 by 7, which gives us 63. This is fairly straight forward because the numbers (9 and 7) are quite small.
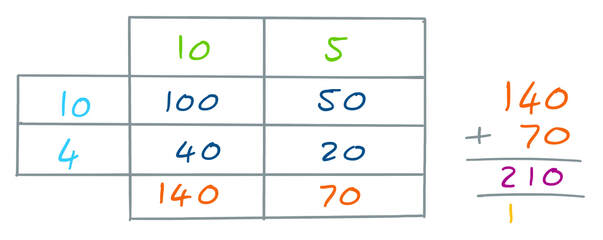
For the denominators, we are multiplying 14 by 15. This is considerably harder because the numbers involved are larger. I am going to multiply 14 by 15 by using the grid method. My working is shown below.
We now have our answer which is:
There are no more common factors between 3 and 10, which means that we have the fraction in its simplest form. The answer is 3/10.
Method 2
Let’s now answer this question using the second method – cancelling before multiplying.
The original calculation is shown below.
From looking at all of the numbers, I notice that 7 and 14 have a common factor of 7. Therefore, I am going to cancel/ divide 7 and 14 by 7. The working is shown below:
Our answer is 3/10. We now check whether the fraction can be simplified. There are no common factors between 3 and 10, which means that this fraction is in its simplest form.
This method will always give the answer in its simplest form, which means that you wouldn’t have to check if the fraction can be simplified. However, it is always a good idea to double check whether the fraction can be simplified as you may have missed some factors when cancelling at the start of the question.
From comparing both methods used to answer this question, you can see that the second method is faster, easier and you are less likely to make a mistake when using this method. Therefore, I would definitely recommend using this method.
Do not use a calculator to answer this question.
Complete the calculation below. Give your answer as a fraction in its simplest form.
From looking at the numbers, I notice that 25 and 10 have a common factor of 5. Therefore, I am going to cancel/ divide 25 and 10 by 5. The working is shown below:
We shouldn’t be able to simplify the fraction if we have done the cancelling at the start correctly. However, it is always best to check that the fraction cannot be simplified. There are no common factors between 12 and 35, which means that this fraction is in its simplest form. The answer to this question is 12/35.
Do not use a calculator to answer this question.
Complete the calculation below. Give your answer as a fraction in its simplest form.
From looking at the fractions, we can see that the first fraction can simplified, and we can simplify it by dividing the numerator and denominator of the fraction by 2. The fractions become:
I am now going to check whether this fraction can be simplified (which it shouldn’t be able to if we have cancelled the fractions at the start correctly). There are no common factors between the numerator (3) and the denominator (11), which means that this fraction is in its simplest form. Therefore, the answer to this question is 3/11.
This cancelling method prior to multiplying fractions may seem fairly confusing to start with, but it makes multiplying fractions with large numerators and denominators without a calculator so much easier to answer. Therefore, it is definitely worth learning this method. There are quite a few questions in the quiz for you to have a go at. There are also worked solutions for all of the questions, so if you want a little bit of help/ if you get stuck, you can use the worked solutions to help you.
Also, the process for this method is exactly the same if we are multiplying 3 fractions together. We cancel the fractions by any common factors between all of the numerators and all of the denominators. We then multiply the fractions across in the usual way. There are two questions in the quiz where 3 fractions are multiplied.