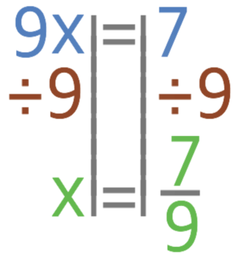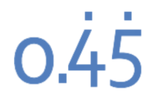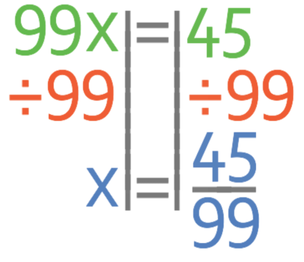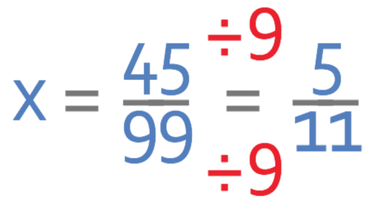Back to Edexcel Fractions (H) Home
1.3 R) Converting Recurring Decimals to Fractions – Part 1
1.3 R) Converting Recurring Decimals to Fractions – Part 1
What are Recurring Decimals?
A recurring decimal is a decimal where a figure or group of figures repeat themselves indefinitely. We denote a recurring figure by placing a dot above the figure that recurs. For example:
A recurring decimal is a decimal where a figure or group of figures repeat themselves indefinitely. We denote a recurring figure by placing a dot above the figure that recurs. For example:
The dot on top of the 3 means that the 3 keeps repeating indefinitely. If we were to write this number out with a some more digits, the number would be:
The 3’s for this number will keep on going forever.
Sometimes it will be the case that there will be a group of figures that will recur. We show that this is the case by placing a dot above the first digit in the repeating group of figures and then another dot above the final digit in the repeating group of figures. An example of where this is the case is:
Sometimes it will be the case that there will be a group of figures that will recur. We show that this is the case by placing a dot above the first digit in the repeating group of figures and then another dot above the final digit in the repeating group of figures. An example of where this is the case is:
The decimal above has a recurring group of 462. If we were to write this number out with a few more digits, it would be:
Converting Recurring Numbers to Fractions
We are now going to have a look at a few examples where we convert a recurring number into a fraction. The process that we use is best explained through some examples. Also, the process is quite tricky, so you may need to go through the examples a few times before you feel fully comfortable answering these types of questions.
Example 1
Convert the number below into a fraction.
We are now going to have a look at a few examples where we convert a recurring number into a fraction. The process that we use is best explained through some examples. Also, the process is quite tricky, so you may need to go through the examples a few times before you feel fully comfortable answering these types of questions.
Example 1
Convert the number below into a fraction.
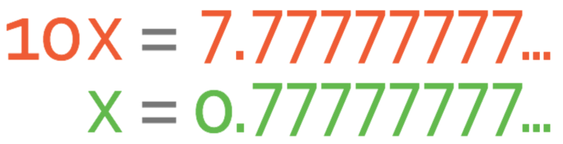
The first step in converting this into a fraction is to let x equal the number and to write the number out with a few more digits. It is the 7 that is recurring, so I am going to write this number out with quite a few 7’s (it does not matter how many 7’s you write out). This gives us the equation:
The next step is to multiply x by 10 to give us 10x.
We are now going to take x from 10x and before we do this, I am going to write x out again below the 10x. This gives us:
The reason why I am writing x out below the 10x is because I am going to take x from 10x by using column subtraction. When we use column subtraction, you can see that all of the 7’s in the decimal positions cancel each other out. This results in us getting just 7 on the right side of the equation.
The value of x is our fraction. Currently we have 9x and we want to find the value of x. Therefore, we need to divide both sides of the equation by 9 (the coefficient of x).
We now have x as a fraction. We now need to check whether this fraction is in its simplest form, which we do by looking for common factors between the numerator and the denominator. There are no common factors between 7 and 9, which means that the fraction is already in its simplest form.
The converting of a recurring number to a fraction always involves multiplying x by a multiple of 10; for this question we multiplied x by 10. The whole point of multiplying x by a multiple of 10 is to get the recurring part of the numbers to over lay one another (preferable in the decimal positions). When this is the case, we can take some value of x to eliminate the recurring part of the numbers. This will all make much more sense when we have a look at few more examples.
The converting of a recurring number to a fraction always involves multiplying x by a multiple of 10; for this question we multiplied x by 10. The whole point of multiplying x by a multiple of 10 is to get the recurring part of the numbers to over lay one another (preferable in the decimal positions). When this is the case, we can take some value of x to eliminate the recurring part of the numbers. This will all make much more sense when we have a look at few more examples.
Example 2
Convert the number below into a fraction.
Convert the number below into a fraction.
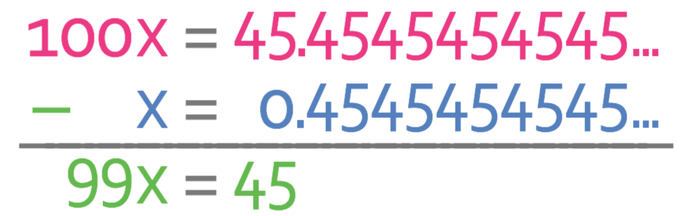
The first step is to let x equal this number and to write out the number with a few more of the recurring digits. The two dots above the number indicates that we have a recurring group of figures and the recurring group of figures is the 4 and the 5. This gives us the equation:
We now need to multiply x by a multiple of 10 so that the recurring part of x and the multiple of 10 lots of x overlap one another. The recurring part of our decimal has 2 digits. Therefore, we need to multiply it by 100 so that the recurring parts overlap. When we multiply x by 100 we get:
From the working above, you can see that the recurring parts of 100x and x overlap one another on the decimal positions. This means that we can take x from 100x and the recurring figures in the decimal positions will be eliminated. In order to column subtract, I am going to write x underneath 100x. The working and the outcome of the column subtraction is shown below.
The value of x is our fraction and currently we have 99x. Therefore, we need to divide both sides of the equation by 99.
We now need to check whether this fraction is in its simplest form, which we do by looking for common factors between the numerator and the denominator. There is a common factor of 9 between 45 and 99. Therefore, we divide both the numerator and the denominator of the fraction by 9.
There are no more common factors between 5 and 11, thus meaning that this fraction is in its simplest form.