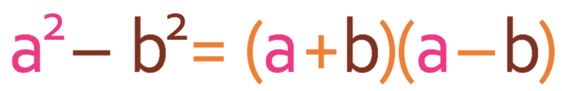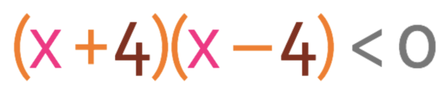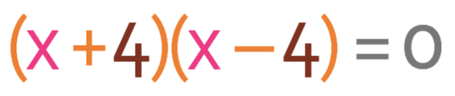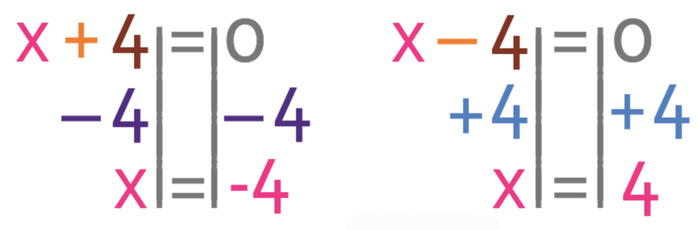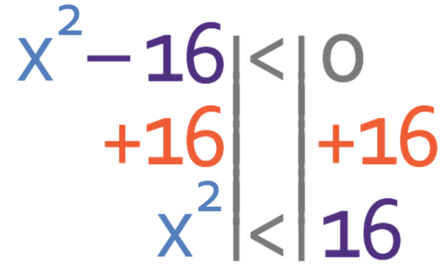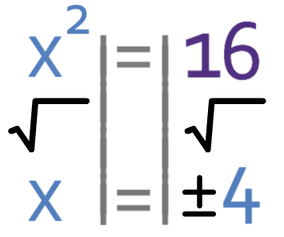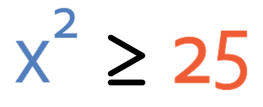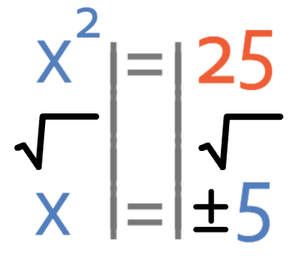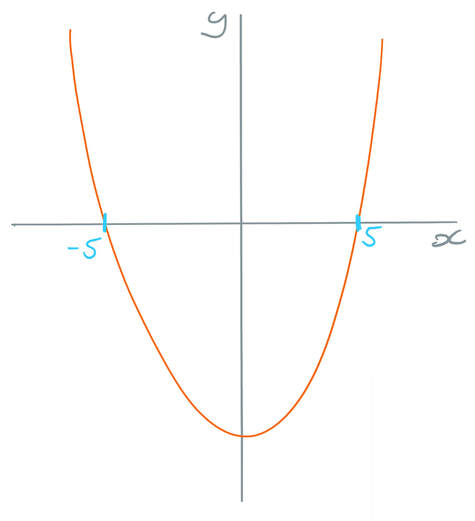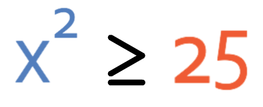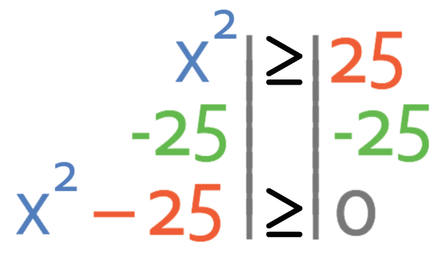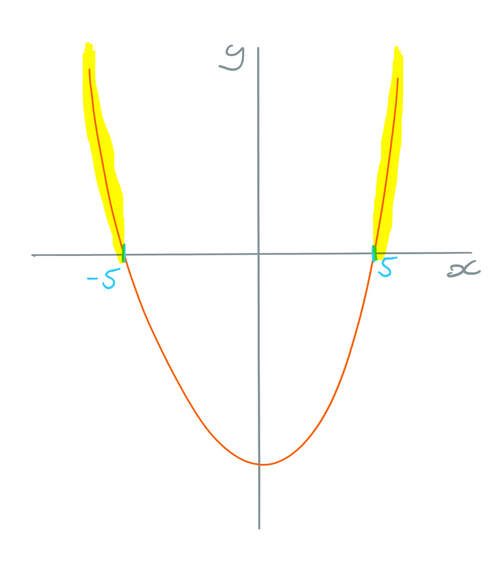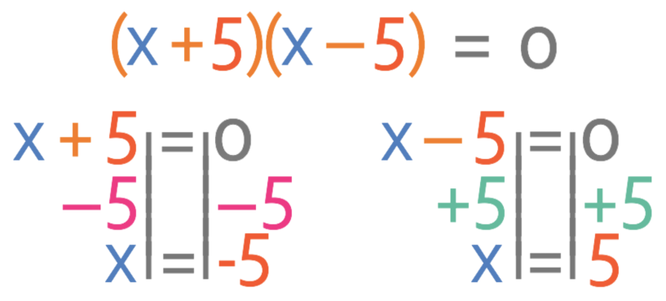Back to Edexcel Inequalities (H) Home
1.5 G) Solving Quadratic Inequalities – Part 1
1.5 G) Solving Quadratic Inequalities – Part 1
Quadratic inequalities are so much easier to answer by sketching the graph. In order to draw a sketch of the graph, we need to find the roots for the quadratic (the roots are where the curve passes through the x axis). There are a few different ways to find the roots depending on the quadratic inequality that we are given.
After we have found the roots for the quadratic inequalities, we can sketch the curve. The final step is to find the values where the graph works for the inequality given at the start of the question. If the quadratic inequality is greater than 0 (>), we will be giving the x values that give a positive value for y; any values for x where the curve is above the x axis. If the quadratic inequality is less than 0 (<), we will be giving the x values whereby the curve is below the x axis. If the inequality includes “or equal to”, the inequality that we give will include equal to/ the roots will be included.
This will all make a lot more sense after we have gone through a few examples. Quadratic inequalities are quite complex. Therefore, you may need to go through the examples in this section and the next section a few times before you feel fully comfortable with them.
- If we have a quadratic term and a number, we can obtain the roots by getting all of the terms to one side of the inequality and factorising by using the difference of two squares. Or we can obtain the roots by manipulating the inequality so that we have the square term on one side and the number on the other side. We then square root both sides. This will be the case for the examples in this section.
- If we have a quadratic term, a linear term and a number, we can find the roots by getting all of the terms to one side of the inequality, factorising and then solving. This will be the case for the examples in the next section.
After we have found the roots for the quadratic inequalities, we can sketch the curve. The final step is to find the values where the graph works for the inequality given at the start of the question. If the quadratic inequality is greater than 0 (>), we will be giving the x values that give a positive value for y; any values for x where the curve is above the x axis. If the quadratic inequality is less than 0 (<), we will be giving the x values whereby the curve is below the x axis. If the inequality includes “or equal to”, the inequality that we give will include equal to/ the roots will be included.
This will all make a lot more sense after we have gone through a few examples. Quadratic inequalities are quite complex. Therefore, you may need to go through the examples in this section and the next section a few times before you feel fully comfortable with them.
Example 1
Solve the quadratic inequality below.
Solve the quadratic inequality below.
The first step in solving quadratic inequalities is to sketch the curve. In order to sketch the curve, we need to find the roots for the curve. There is a quadratic term and a number in this inequality. This means that we can find the roots in two ways.
Method 1: Difference of Two Squares
One way is to factorise by using the difference of two squares. The formula for the difference of two squares is shown below:
Method 1: Difference of Two Squares
One way is to factorise by using the difference of two squares. The formula for the difference of two squares is shown below:
In our inequality, a2 is x2, which means that a is x, and b2 is 16, which means that b is 4. This means that our factorised quadratic is:
The next step is to change the inequality sign to an equals sign and solve.
In order for this factorised quadratic to equal 0, either the first bracket must equal 0, or the second bracket must equal 0. We let each of these brackets equal 0 to find the solutions for x (the roots). The working is shown below:
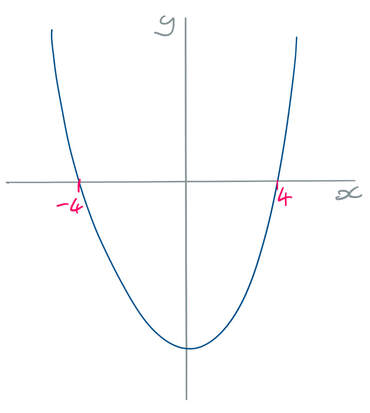
The two roots for the quadratic are where x is -4 and 4. This means that we can do a quick sketch of the curve. My sketch is shown below.
The final step is to find the values for x that satisfy the original inequality. The original inequality is shown below:
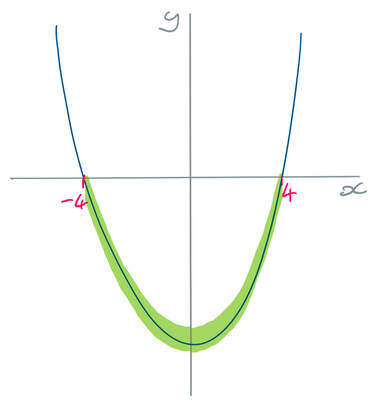
The original inequality says that the quadratic is less than zero. This means that we are looking for the values of x that give a negative value for y; this is the part of the curve that is below the x axis. There is one part of the curve that is negative, and I have highlighted this part on the graph below.
By looking at the graph, we can see that x values between -4 and 4 give us a negative value for y. This means that the solutions for our inequality are:
Method 2: Square Rooting
We obtained the roots for our inequality by factorising. Another way that we could have found the roots for the quadratic is to move the number across to the other side of the inequality and then square root both sides. The original inequality is given below:
We obtained the roots for our inequality by factorising. Another way that we could have found the roots for the quadratic is to move the number across to the other side of the inequality and then square root both sides. The original inequality is given below:
We move the -16 from the left side of the inequality to the right by adding 16 to both sides.
I am now going to change the inequality to an equal signs and square root both sides. When we square root a number, we obtain the positive and negative value (±).
This tells that we have two roots; one at 4 and one at -4. From this information, we can sketch the graph and solve the inequality in the same way as before.
Example 2
Solve the quadratic inequality.
Solve the quadratic inequality.
The first step in solving quadratic inequality is to find the roots for the quadratic. This quadratic inequality contains a square term and a number (there are no linear terms [x]). This means that we find the roots for the quadratic by either factorising using the difference of two squares, or by getting the square term to one side and the number term to the other side, and then square rooting.
Currently, we have the square term on one side and the number on the other side. Therefore, I am going to find the roots by square rooting both sides of the inequality. Before I square root both sides, I am going to change the inequality sign to an equals sign. Also, when we square root a number, we need to remember that we will obtain a positive and negative root.
Currently, we have the square term on one side and the number on the other side. Therefore, I am going to find the roots by square rooting both sides of the inequality. Before I square root both sides, I am going to change the inequality sign to an equals sign. Also, when we square root a number, we need to remember that we will obtain a positive and negative root.
The two roots for the quadratic are where x is 5 and -5. This means that we are able to sketch the graph. The sketch only needs to be a quick sketch and my sketch is given below.
We now need to find where the graph satisfies the original inequality. The original inequality is given below.
Currently the inequality has terms on both sides, which can make it tricky to know what region we are looking for on the graph. The easiest way to know the region that we are looking for on the graph is to get all of the terms to one side of the inequality and to have a positive number of the quadratic terms (x2). Currently, we have an x2 on the left, so I am going to get all of my terms to the left side of the inequality. I am able to do this by taking 25 from both sides of the inequality.
This now tells us that we are looking for the parts of the curve where the curve is positive (above the x axis) or equal to 0 (on the x axis). There are two different parts of the curve where this is the case and I have highlighted these parts on the graph below.
We now need to create an inequality for the x values for each of these sections. The inequalities are:
The inequalities for the solutions contain “or equal to” because the inequality at the start of the question included “or equal to”.
We could have found the roots by factorising the quadratic by using the difference of two squares technique. In order to use this technique, we would need to have all of the terms on one side of the inequality and 0 on the other side. We would use the inequality that is shown below.
We could have found the roots by factorising the quadratic by using the difference of two squares technique. In order to use this technique, we would need to have all of the terms on one side of the inequality and 0 on the other side. We would use the inequality that is shown below.
We can now factorise and solve to find the roots. The working is shown below.
The roots are 5 and -5. These are the same roots that we found earlier.