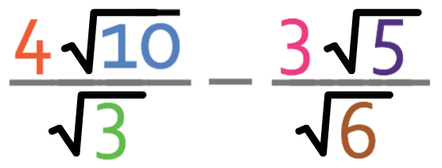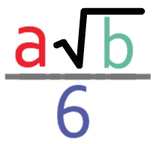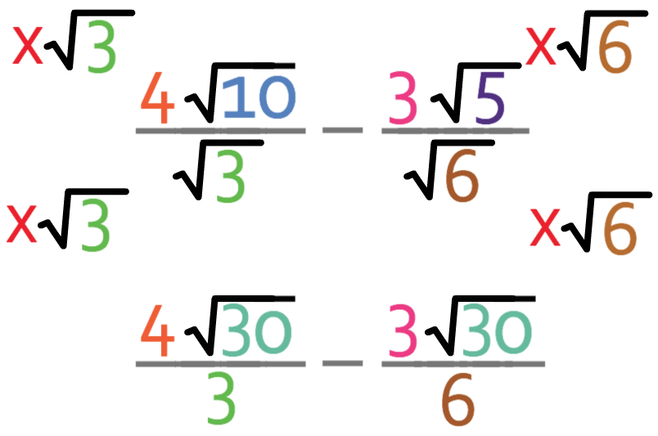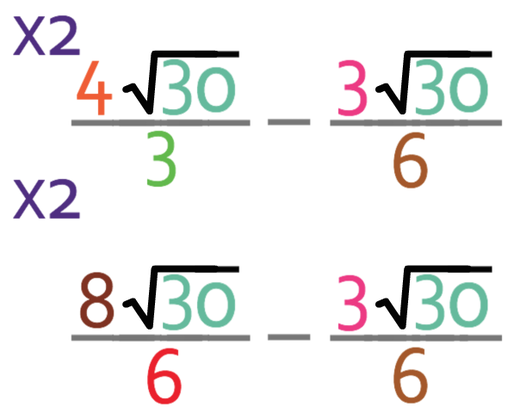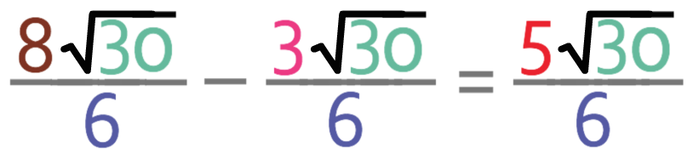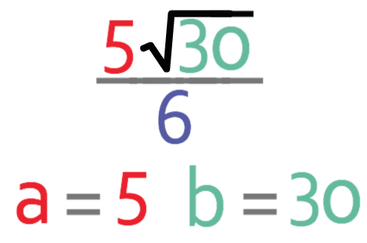Back to Edexcel Surds (H) Home
1.8 J) Calculations Involving Surds
1.8 J) Calculations Involving Surds
General calculations can be made harder by surds being involved. For example, a fraction calculation can be made harder by having a surd in one or both of the fractions. The best way to answer these types of questions is to think about the rules or methods used to answer the calculation if the surds weren’t involved, and then use those rules or methods with the surds being involved; essentially, do not get scared with the surds being present in the question.
For example, the rules for adding fractions is that the denominators of the fractions must be the same. This will always be the case even if there are surds in the fractions.
Also, if we are multiplying fractions, the rule is that we multiply straight across; we would multiply the numerators to obtain the numerator in the answer, and we would multiply the denominators to obtain the denominator in the answer. This will always be the case even if there are surds in the fractions.
In this section, we are going to look at an example where fractions are being taken away from one another and the fractions involved contain surds. Before giving this example a go, make sure that you are comfortable with the rest of the surds content.
For example, the rules for adding fractions is that the denominators of the fractions must be the same. This will always be the case even if there are surds in the fractions.
Also, if we are multiplying fractions, the rule is that we multiply straight across; we would multiply the numerators to obtain the numerator in the answer, and we would multiply the denominators to obtain the denominator in the answer. This will always be the case even if there are surds in the fractions.
In this section, we are going to look at an example where fractions are being taken away from one another and the fractions involved contain surds. Before giving this example a go, make sure that you are comfortable with the rest of the surds content.
Example 1
Show that
Show that
can be written in the form
where a and b are integers.
We are taking fractions, and when we take fractions, the denominators of the fractions need to be the same. Currently, both of these fractions have a surd as their denominator. We never like to have surds on the denominators of fractions, and this is why I am going to rationalise both of the fractions. After we have rationalised the fractions, we can then make the denominators the same.
Both of these fractions have a single surd as their denominator. Therefore, we can rationalise the fractions by multiplying the numerator and the denominator of the fraction by the surd that is on the denominator of the fraction. Therefore, we multiply the numerator and denominator of the first fraction by √3, and we multiply the numerator and denominator of the second fraction by √6.
We are taking fractions, and when we take fractions, the denominators of the fractions need to be the same. Currently, both of these fractions have a surd as their denominator. We never like to have surds on the denominators of fractions, and this is why I am going to rationalise both of the fractions. After we have rationalised the fractions, we can then make the denominators the same.
Both of these fractions have a single surd as their denominator. Therefore, we can rationalise the fractions by multiplying the numerator and the denominator of the fraction by the surd that is on the denominator of the fraction. Therefore, we multiply the numerator and denominator of the first fraction by √3, and we multiply the numerator and denominator of the second fraction by √6.
There are now no surds on the denominators of both of the fractions, which means that we have successfully rationalised the denominators.
We now need to make the denominators of the fractions the same because when we take fraction, the denominators of the fractions need to be the same. Currently the denominator of the first fraction is 3 and the denominator of the second fraction is 6. 3 and 6 both go into 6, so I am going to make both of the denominators 6.
The denominator of the first fraction is 3 and we are able to make it 6 by multiplying the numerator and the denominator of the fraction by 2. The denominator of the second fraction is already 6, so we do not need to do anything with this fraction.
We now need to make the denominators of the fractions the same because when we take fraction, the denominators of the fractions need to be the same. Currently the denominator of the first fraction is 3 and the denominator of the second fraction is 6. 3 and 6 both go into 6, so I am going to make both of the denominators 6.
The denominator of the first fraction is 3 and we are able to make it 6 by multiplying the numerator and the denominator of the fraction by 2. The denominator of the second fraction is already 6, so we do not need to do anything with this fraction.
The denominators of the fractions are the same, which means that we can complete the calculation. When we subtract fractions, we subtract the numerators and keep the denominator the same.
For the subtraction of numerators, we are doing the calculation 8√30 – 3√30. Both of the surds are √30, which means that we can complete the calculation by imagining that the surd (√30) is an unknown (such as x). By imagining that the surd is an unknown, it means that we have 8 unknowns and we are taking 3 unknowns away, which leaves us with 5 unknowns (8x – 3x = 5x). We then replace the unknown with √30, which results in the answer being 5√30; the numerator of the fraction is 5√30.
The denominator stays the same, which means that the denominator of the fraction is 6.
For the subtraction of numerators, we are doing the calculation 8√30 – 3√30. Both of the surds are √30, which means that we can complete the calculation by imagining that the surd (√30) is an unknown (such as x). By imagining that the surd is an unknown, it means that we have 8 unknowns and we are taking 3 unknowns away, which leaves us with 5 unknowns (8x – 3x = 5x). We then replace the unknown with √30, which results in the answer being 5√30; the numerator of the fraction is 5√30.
The denominator stays the same, which means that the denominator of the fraction is 6.
The final step is to check whether the surd and fraction can be simplified. The surd cannot be simplified as there are no square factors in 30. And, the fraction cannot be simplified because there are no common factors between the numerator and denominator.
We now have our final answer. Next to my answer I would put what the values of a and b are; a is 5 and b is 30.
We now have our final answer. Next to my answer I would put what the values of a and b are; a is 5 and b is 30.