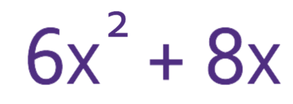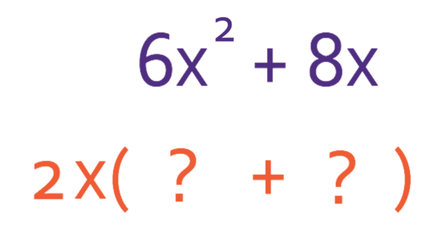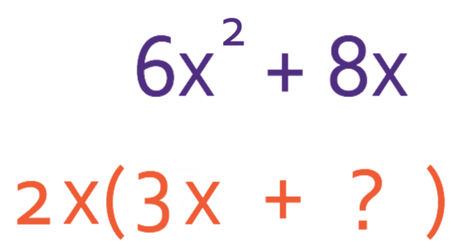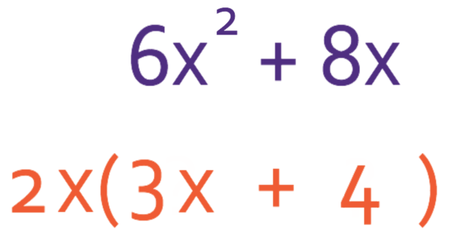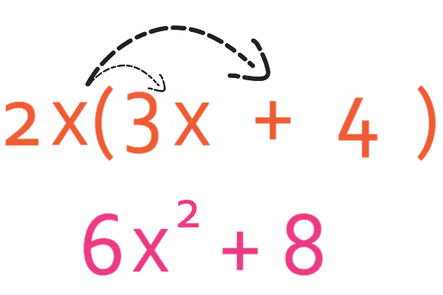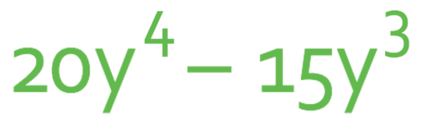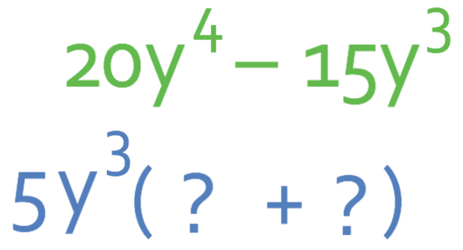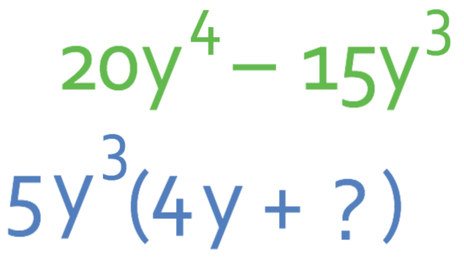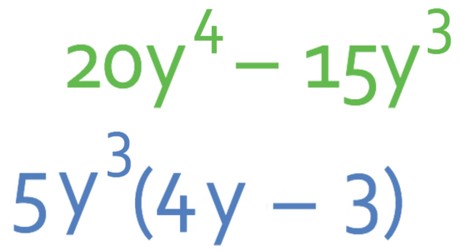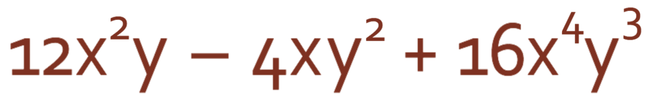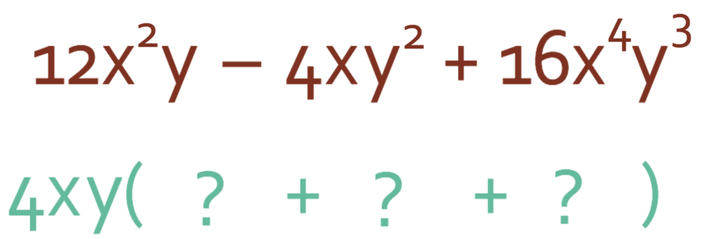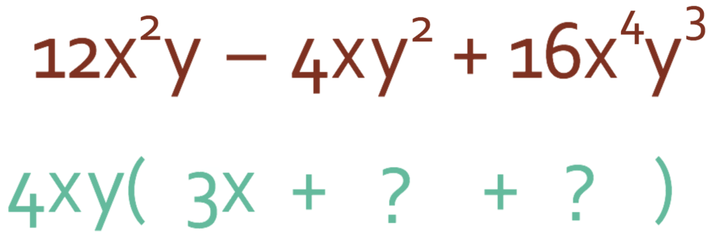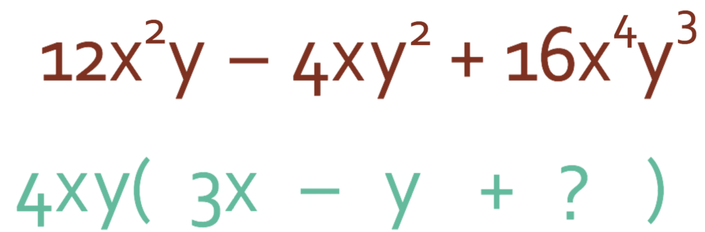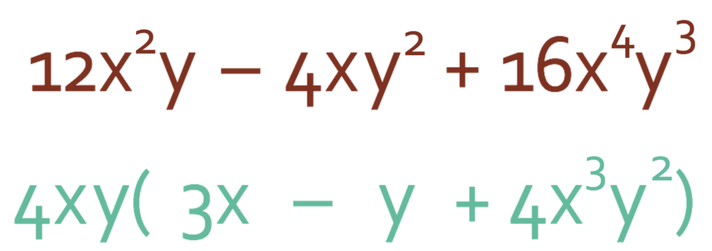2.1 J) Factorising
Factorising is the opposite of expanding. In order to factorise an expression, we take out the highest common factor of all of the terms in the expression (the highest common factor is the largest factor that goes into all of the terms in an expression). The best way to find the highest common factor in an expression with numbers and unknowns is to find the highest common factor for the numbers, then the highest common factor for the unknowns (if there are more than one unknown, it is easier to find the highest common factor for the unknowns separately). We then combine each of the highest common factors to give us the highest common factor in the expression.
After we have found the highest factor, we place the highest common factor on the outside of the brackets. We then work out what we need to multiply the highest common factor by to obtain each of the terms that are in the expression and we place these values inside the brackets.
Let’s have an example.
Example 1
Factorise the expression below.
The expression above has both numbers and one unknown (x). Therefore, I think that the best way to find the highest common factor between the two terms is to find the highest common factor for the numbers and the highest common factor for the x’s. After we have found both of these, we can combine them to give us the highest common factor overall.
The numbers in the expression are 6 and 8. The highest common factor between these two numbers is 2. For the x’s, the first term has an x2 and the second term has an x. Therefore, the highest common factor for the x’s is x. We can combine both of these to say that the highest common factor in the expression is 2x.
This means that 2x will be on the outside of the bracket. We now need to find what will be on the inside of the brackets. As there are two terms in our expression, we are going to have two terms inside the bracket.
We find the first term by seeing what we need to multiply by 2x to give us 6x2 (another way to view this is to divide the first term by 2x). You may find it easier to split it up into numbers and unknowns. The number in the expression is 6. In order to obtain 6, we multiply the 2 that is outside the bracket by 3. The x term inside the bracket is x2. In order to obtain x2, we multiply the x that is outside the bracket by x. Therefore, the first term in the bracket is 3x.
We now need to find the second term in the bracket, which we do by finding out what we need to multiply by 2x to give us 8x (we could also find the value by dividing 8x by 2x). Either way, we find that the second term in the bracket is 4.
When we have factorised, it is always a good idea to check if there are any more common factors between the terms that are on the inside of the brackets. If you do find any common factors, you should take these factors out of the bracket. There are no common factors between 3x and 4, which means that we have factorised correctly.
Also, if we want to check that we have factorised correctly, we can expand the brackets to check that it gives us the expression that we started with.
When we expand the brackets, we obtain the expression that we started with and this means that we have factorised correctly.
Example 2
Factorise the expression below.
Both of the terms in the above expression have a number and a y component. Therefore, the best way to find the highest common factor for both of the terms is to find the highest common factor for the numbers and the unknowns separately, and then combine each of them together to get the overall highest common factor.
The numbers in the expression are 20 and -15 (or 15; it is easier to ignore the signs when finding the highest common factors for the numbers). The highest common factor between these two numbers is 5.
The next step is to find the highest common factor between the unknowns; we are looking for the highest common factor between y4 and y3. The highest common factor for any unknown is the term that has the smallest power. For y4 and y3 the smallest power is y3. Therefore, the highest common factor for the y’s is y3.
The final step is to combine both the highest common factors for the numbers and the y’s to get the overall highest common factor. Therefore, the highest common factor for the expression is 5y3. We now place this outside the bracket.
We are now ready to find the terms inside the bracket. The first term in the bracket is going to be what we need to multiply 5y3 by to get 20y4. It is easier to split this up into numbers and unknowns/ y’s.
Let’s start with the numbers. In order to obtain 20, we need to multiply 5 by 4.
Let’s move onto the unknowns. In order to obtain y4, we need to multiply y3 by y.
This results in the first term in the bracket being 4y.
We now need to find the second term in the bracket, which is what we need to multiply 5y3 to obtain –15y3.
Let’s start with the sign. In order to obtain a negative, we need to second term inside the bracket to be negative.
The next step is to look at the numbers. In order to obtain 15, we need to multiply 5 by 3.
The final step is to move onto the y’s. The final term has a y3 and when we multiply y3 on the outside of the bracket by something, we will get y3. Therefore, there are no y’s in the second term inside the bracket.
We now combine all of these together and this results in the second term in the bracket being -5.
We can expand the bracket above to see if we have factorised correctly (I am not going to do this, but you could try expanding the brackets out to see if we get the expression that we started with).
Example 3
Factorise the expression below.
The first step to factorising this expression is to find the highest common factor between all of the terms. The easiest way to do this is to find the highest common factor between the number, then the highest common factor for the x’s and finally the highest common factor for the y’s. We then combine all of these highest common factors to obtain the overall highest common factor for the expression.
The numbers are 12, -4 and 16. The highest common factor for the numbers is 4.
The x’s are x2, x and x4. The highest common factor for the x’s is x (the highest common factor for unknowns will always been the lowest power).
The y’s are y, y2 and y3. The highest common factor for the y’s is y.
The overall highest common factor in the expression is 4xy. 4xy will be on the outside of the bracket. There are 3 terms in the expression, which means that we will have 3 terms inside the brackets. Our factorised brackets will take the form.
We now need to find the three terms inside the bracket. We do this by finding out what we need to multiply 4xy by to give us the three terms that are in the expression; it is best to do this by splitting the three terms up into numbers, x’s and then y’s.
The first term in the bracket is 12x2y. In order to get 12, we multiply 4 (which is outside the bracket) by 3. In order to get x2, we multiply x (outside the bracket) by x. The first term in the brackets will not contain any y’s because the y in 12x2y will be there because of the y that is on the outside of the bracket. Therefore, the first term inside the bracket is 3x.
We now move onto finding what we need to multiply 4xy by to get -4xy2. In order to get -4, we multiply 4 by -1. The second term in the bracket will not contain any x’s because the x in -4xy2 will be there because of the x that is on the outside of the bracket. To obtain y2, we multiply the y that is on the outside of the bracket by y. Therefore, the second term inside the bracket is -1y, which we can just write as -y (there is no need for the 1 in front on the y).
We are now onto the final term in the bracket. The final term in the expression is 16x4y3. Therefore, we are looking to find what we need to multiply by 4xy needs to give us 16x4y3. In order to obtain 16, we need to multiply the 4 that is on the outside of the bracket by 4. In order to obtain x4, we need to multiply x that is outside the bracket by x3. And finally, in order to obtain y3, we need to multiply y that is on the outside of the bracket by y2. Therefore, the final term in the bracket is 4x3y2.
There are no common factors on the inside of the bracket, which means that we have factorised out all of the common factors.
We are able to check that we have factorised correctly by expanding out the brackets and checking that we obtain the expression that we were factorising. I am not going to do this, but feel free to expand the bracket to check.