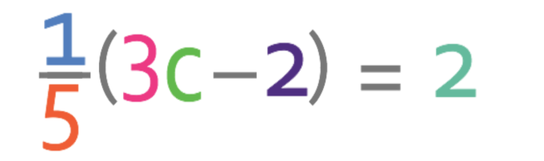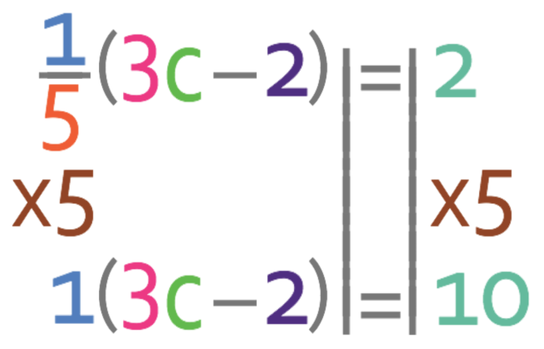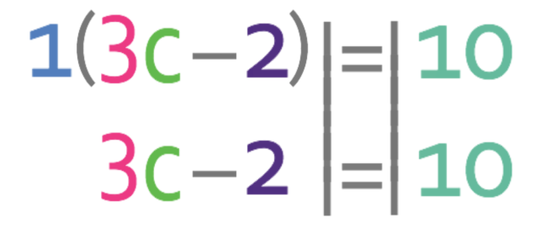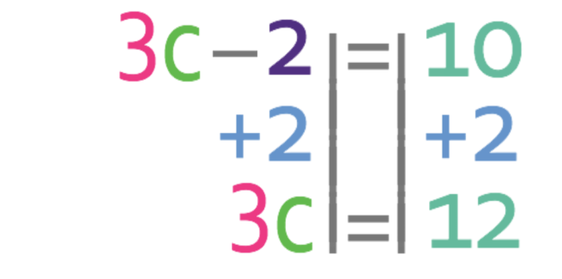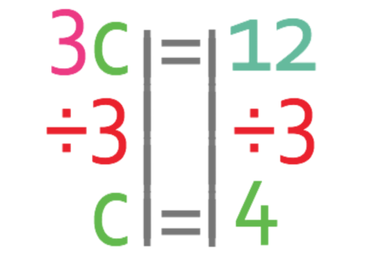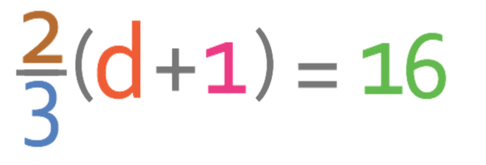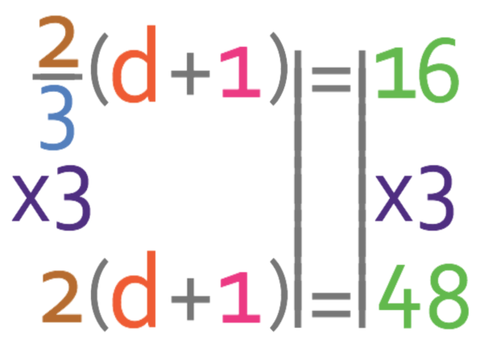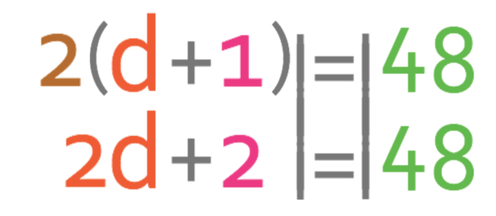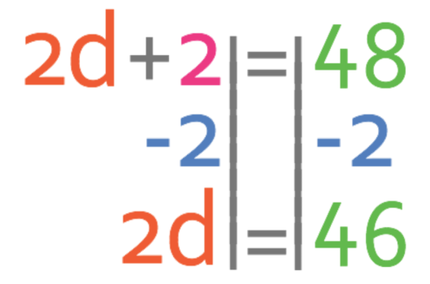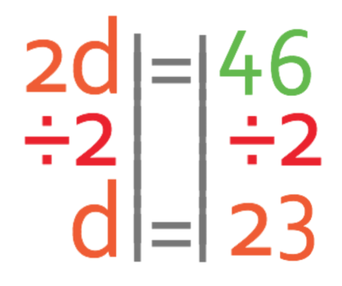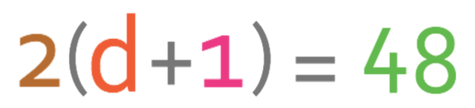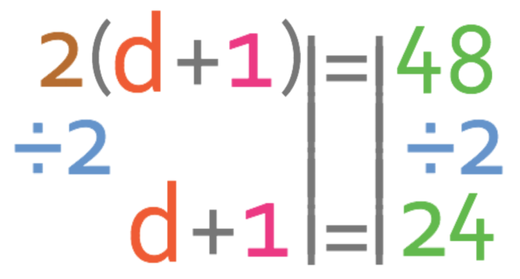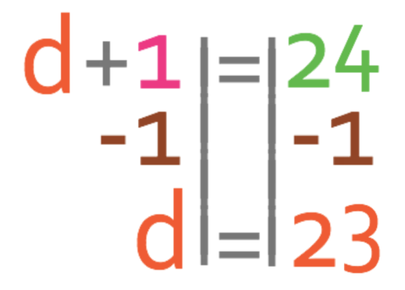Back to Edexcel Linear Equations (H) Home
2.2 E) Linear Equations: Solving when Expanding Brackets – Part 2
2.2 E) Linear Equations: Solving when Expanding Brackets – Part 2
The content in this section builds on the content that was discussed in the previous section. Make sure that you have covered the previous section before coming on to this section (click here to be taken through to the previous section).
Example 1
Find the value of c.
Find the value of c.
We could expand the bracket on the left side of the equation. However, it would get quite messy with a lot of fractions. Therefore, when we have an equation like this, the best way to solve it is to multiply both sides of the equation by the denominator of the fraction that is outside the bracket. By doing this we eliminate the fraction from the outside of the bracket, thus making it easier to solve the equation.
The denominator of the fraction outside the bracket on the left is 5, so we multiply both sides of the equation by 5.
The denominator of the fraction outside the bracket on the left is 5, so we multiply both sides of the equation by 5.
Multiplying a bracket by 1 results in the bracket staying the same.
We now need to get all of the unknowns to one side of the equation and all of the numbers to the other side. We get all of the unknowns to the side that has more unknowns. Currently the left side of the equation has more c’s than the right side (the left side has 3c and the right side has 0c). Therefore, we want to have all of the c’s on the left and all of the numbers on the right. This means that we need to move the -2 from the left side to the right. We are able to do this by adding 2 to both sides of the equation.
Currently we have the value of 3c, but we want to find the value of c. Therefore, we divide both sides by 3.
This tells us that c is 4.
We can check we have the correct value by subbing in c as 4 into the first equation.
We can check we have the correct value by subbing in c as 4 into the first equation.
This equation works, which means that we have the correct value for c; c is 4.
Example 2
Find the value of d.
Find the value of d.
Like the question before, I am going to multiply the left and the right side of the equation by the denominator in the fraction next to the brackets. Therefore, I am multiplying both sides by 3.
The next step is to multiply out the brackets on the left side of the equation (we could divide both sides by 2; I will go through this method at the end).
There are more d’s on the left side of the equation than the right, so I am going to have the left side of the equation as the side where I get all of the d’s to, and the right side as the side where I get all of the numbers to. This means that we need to move the +2 that is currently on the left side of the equation to the right. We are able to do by doing the opposite, and the opposite of adding 2 is taking 2; we take 2 from both sides of the equation.
We want to find the value of d and not 2d. Therefore, we divide both sides of the equation by 2.
Therefore, d is equal to 23. We can check that this value is correct by subbing it into the original equation (I am not going to do this, but feel free to check).
After we had multiplied both sides of the equation by the denominator of the fraction outside the bracket (3), I mentioned that there was a second method that we could have used to find the value of d. We are going to go through this method now. The equation that we had after multiplying both sides of the equation by 3 is shown below.
After we had multiplied both sides of the equation by the denominator of the fraction outside the bracket (3), I mentioned that there was a second method that we could have used to find the value of d. We are going to go through this method now. The equation that we had after multiplying both sides of the equation by 3 is shown below.
On the left side of the equation, we have 2 lot of the brackets. We are able to get rid of the 2 lots of the bracket by dividing both sides of the equation by 2.
We now need to move the +1 from the left side of the equation to the right. We are able to do this by doing the opposite and the opposite of adding 1 is taking 1.
Therefore, d is 23, which is exactly the same value that we found when we used the previous method.