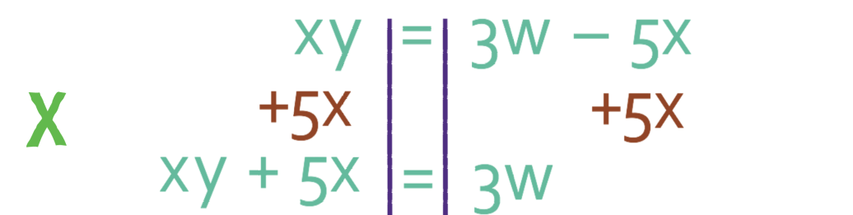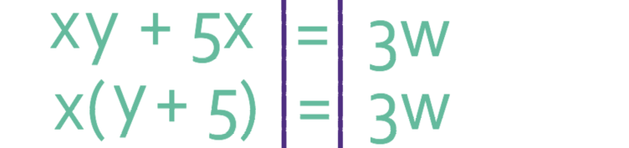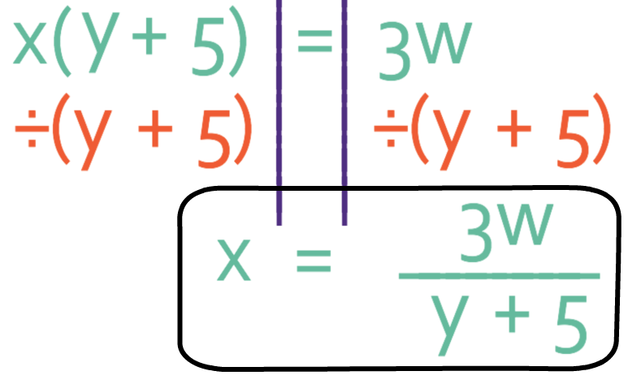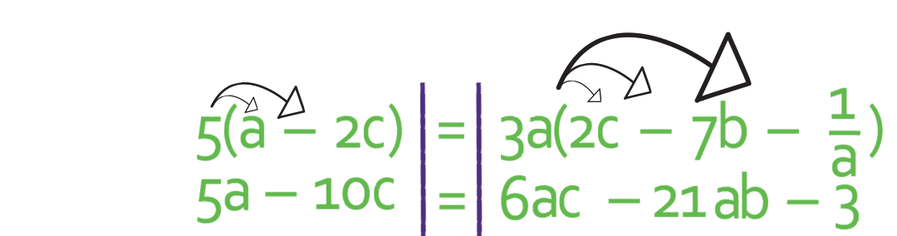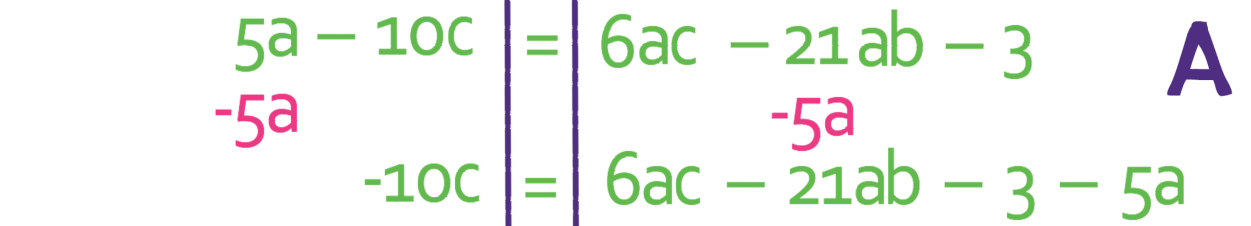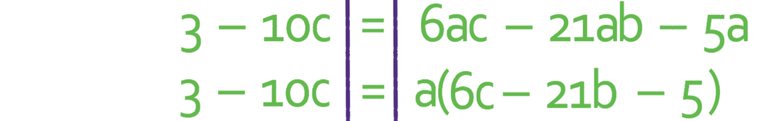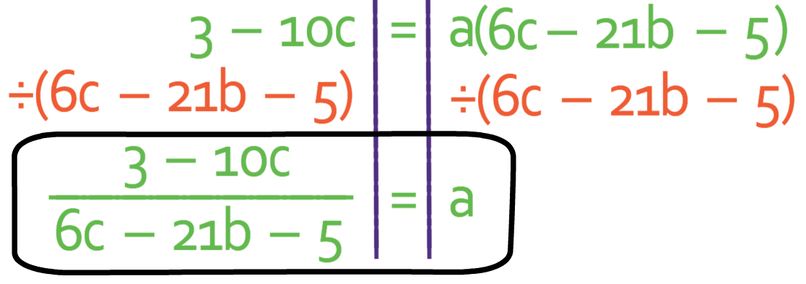Back to Edexcel Algebraic Formulae (H) Home
2.3 D) Rearranging Formulas – Part 2
2.3 D) Rearranging Formulas – Part 2
In this section, we are going to look at some more complex examples of rearranging a formula to make a particular unknown the subject. Therefore, make sure that you have worked through the previous section before working through this one (click here to be taken through to section before this).
The general rules for making an unknown the subject in a more complex formula is given below:
Let’s have a few examples.
The general rules for making an unknown the subject in a more complex formula is given below:
- Get all of the terms that contain the unknown that you want to make the subject on one side of the formula and all of the other terms to the other side of the formula
- Factorise out the variable that you are making the subject
- Divide both sides of the formula by what is inside the bracket
Let’s have a few examples.
Example 1
Make x the subject of the formula below.
Make x the subject of the formula below.
The first step to make x the subject is to get all of the terms that contain x to one side of the formula and all of the all other terms that do not contain any x’s to the other side.
I am going to get all of the terms that contain x to the left side of the formula; it does not matter which side we get all of the x’s to. As I am getting all of the terms that contain x to the left, I need to move the -5x that is currently on the right side of the formula to the left. I am able to do this by doing the opposite; the opposite of taking 5x is adding 5x. Therefore, we add 5x to both sides of the formula.
I am going to get all of the terms that contain x to the left side of the formula; it does not matter which side we get all of the x’s to. As I am getting all of the terms that contain x to the left, I need to move the -5x that is currently on the right side of the formula to the left. I am able to do this by doing the opposite; the opposite of taking 5x is adding 5x. Therefore, we add 5x to both sides of the formula.
The next step is to factorise out x on the left side of the formula. As we are factorising out x, x will be on the outside of the bracket. The inside of the bracket will be what we have to multiply by x to obtain xy + 5x, which is y + 5 (whenever factorising, it is a good idea to multiply out the bracket that you have just created to check that you obtain what you were factorising; if you did not obtain what you were factorising, it would imply that you have done the factorising wrong). The factorise formula becomes.
The final step is to divide both sides by the bracket, which is y + 5.
We now have x as the subject of the formula.
Example 2
Make a the subject of the formula below.
Make a the subject of the formula below.
We are wanting to make a the subject, so we need to get all of the terms that have a in them to one side of the formula and all of the terms that do not have an a in them to the other side of the formula. However, we first need to multiply out the brackets on each side of the formula, so that we can see which terms do have an a in them and which terms do not have an a in them. Whenever we are multiplying out brackets, we need to make sure that the term that is on the outside of the bracket is multiplied by every term that is on the inside of the bracket (you may find it easier to use arrows to make sure that you multiply the term on the outside of the bracket by all of the terms on the inside of the bracket).
The multiplied-out formula becomes.
The multiplied-out formula becomes.
The next step is to get all of the terms that contain a on one side of the formula and all of the terms that do not contain a on the other side of the formula. It does not matter which side of the formula we get all of the terms that contain an a on (it does not matter if we get them all to the right side of the formula or the left side). There are 3 components that have an a in them and 2 of them are already on the right side of the formula. Therefore, I am going to get all of the terms that have an a in them on the right side of the formula and all of the terms that do not have an a in them on the left side.
The only component with an a in it on the left side is 5a and we need to move this component to the right. We do this by doing the opposite, which means that we take 5a from both sides.
The only component with an a in it on the left side is 5a and we need to move this component to the right. We do this by doing the opposite, which means that we take 5a from both sides.
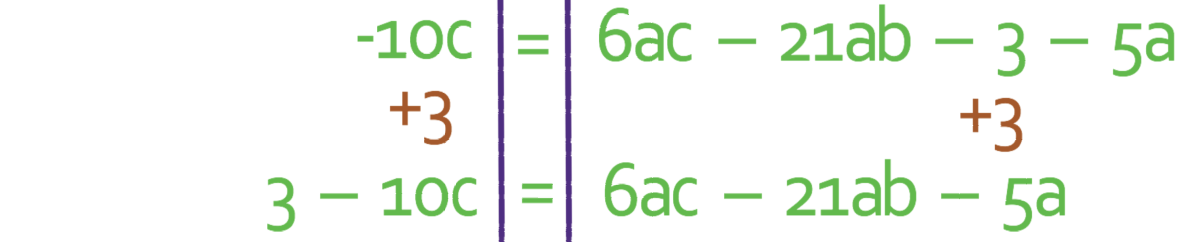
The right side of the formula should only have components that have an a in them. The -3 does not have an a in it, which means that we must move it to the left side of the formula. We do this by adding 3 to both sides. This gives us.
We now have all of the terms with an a in them on the right side of the formula and all of the term that do not have an a in them on the left side. This means that we are ready to factorise a out of the right side of the formula. The factorised version is given below.
The final step is to divide both sides by the bracket, which is 6c – 21b – 5. This give us:
The formula above now has a as its subject