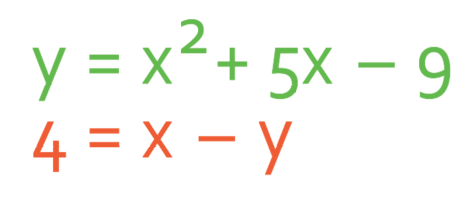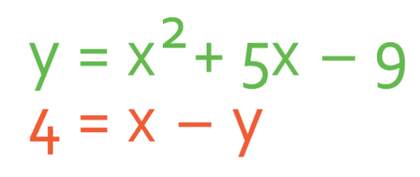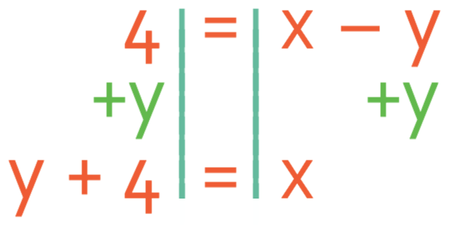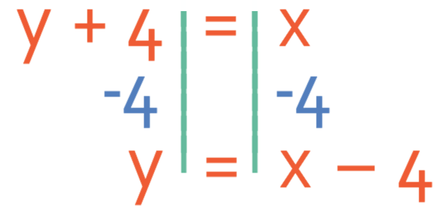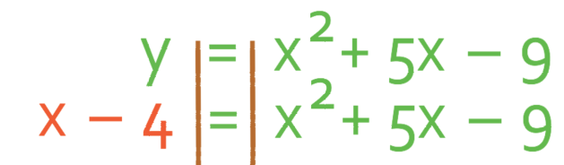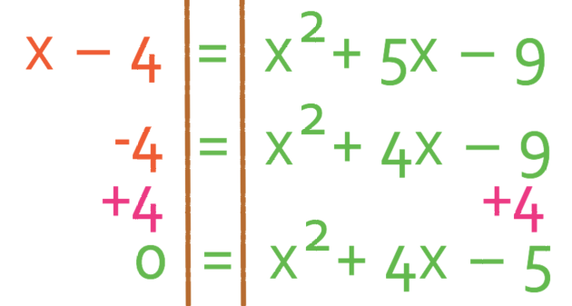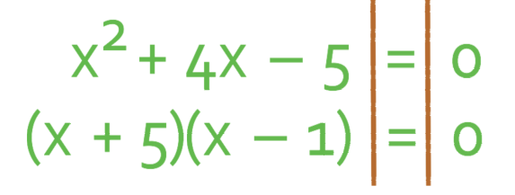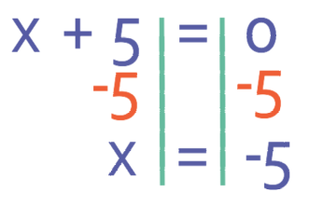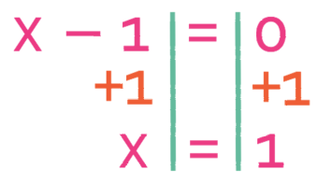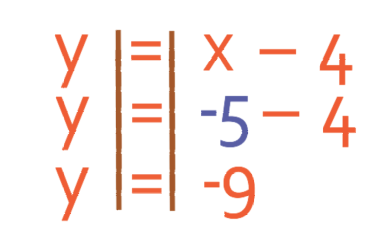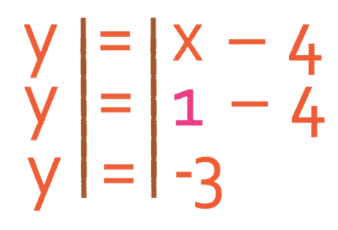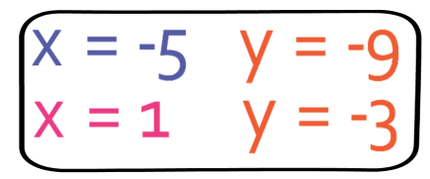2.4 E) Quadratic Simultaneous Equations: Substitution Method
Sometimes we will be given simultaneous equations where one of the equations is a quadratic and the other equation is linear. A linear equation is where the highest power of any of the unknowns is 1 (i.e. just x or y). A quadratic equation is where the highest power of any of the unknowns is 2 (squared; i.e. x2 or y2). For example, solve the simultaneous equation below:
The first equation is a quadratic because it’s highest power of an unknown is 2, and the second equation is linear because the highest power of any of the unknowns is 1.
Example 1
Solve the simultaneous equation:
I am going to solve this simultaneous equation by using the substitution method. The substitution method works by finding a value for one of the unknowns in terms of the other unknown. We do this by making one of the unknowns the subject in one of the equations. We then sub in the expression that we have found for the unknown that we have made the subject into the other equation. By doing this, we get rid of one of the unknowns in the equation leaving just one unknown, thus meaning that we can solve the equation to find the unknown that is left.
I am going to find what y is in terms of x’s and numbers from the second equation and then substitute this into the first equation. After I have substituted y into the first equation, I will have an equation that only has one unknown (x), which means that I can find the value of x.
So, Let’s start by making y the subject in the second equation.
We want to have positive y is equal to something and not negative y. Therefore, the first step in making y the subject is to move the -y from the right side of the equation to the left. We are able to do this by doing the opposite, and the opposite of taking y is adding y; we add y to both sides of the equation.
We now need to get rid of the 4 on the right side of the equation, which we are able to do by taking 4 from both sides of the equation.
We can now sub our expression for y in terms of x and numbers into the first equation.
By subbing our value of y into the first equation we are getting rid of one of the unknowns (y), which leaves us with one unknown, thus meaning that the equation can be solved; the only unknown in the equation is x.
In order to solve a quadratic equation, we need to get all of the terms to one side of the equation. It is always easier to work with a positive number of x2’s. There is only one x2 term in this equation, and it is on the right side of the equation. Therefore, it is best to get all of the terms in the equation to the right. We get the x across by taking x from both sides of the equation, and we get the -4 across by adding 4 to both sides of the equation.
I am now going to swap the sides because I find it easier to have the 0 on the right of the equals rather than the left.
Now that we have all of the terms on one side of the equation, we can find the value of x by factorising. We are going to be factoring with double brackets as it is a quadratic. Quadratic equations take the form of ax2 + bx + c. For our equation, the value of a is 1, b is 4 and c is -5. As the value of a is 1 (it is singular x2), we factorise by looking for two numbers that multiply to give -5 (the value of c) and add together to give 4 (the value of b). Here is a list of numbers that multiply together to give -5:
> 5 and -1
> -5 and 1
The only pair of numbers that adds to give 4 is 5 and -1. Therefore, the factorised equation becomes:
In order for the left side of the equation to be 0, one of the brackets must equal 0. Therefore, we let each of the brackets equal 0. Let’s let the first bracket equal 0.
One value for x is -5.
We now do the same for the second bracket.
So, our two values for x are -5 and 1. To find the value of y we sub the values of x that we have found into one of the equations. It is easier to use the second equation as it is linear as opposed to using the first equation, which is a quadratic (it does not matter what equation you sub the values for x into to find y, but the second equation has fewer terms and lower powers meaning that it will be easier and quicker). I am going to use the rearranged form of equation 2 where y was the subject. This is because it will be easier to find the value of y using the rearranged equation. The rearranged equation is:
Let’s sub in x as -5 first.
Therefore, one set of solutions is x is -5 and y is -9.
We find the next set of solutions by subbing in x as 1.
Therefore, our two pairs of solutions are:
We can sub in these values for the first equation to see if the equation works.
x = -5 and y = -9
y = x 2 + 5 x – 9
-9 =(-5)2 + 5(-5) – 9
-9 = 25 – 25 – 9
-9 = -9
And for the other values. x = 1 and y = -3
y = x 2 + 5 x – 9
-3 = 12 + 5(1) – 9
-3 = 1 + 5 – 9
-3 = -3
Both of the pairs of values for x and y work in the equation, which means that we have found the correct values for x and y.