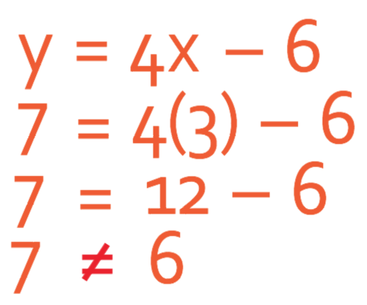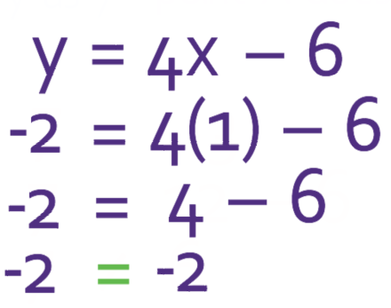Back to Edexcel Linear Graphs (H) Home
2.5 E) Checking a Point Lies on a Line
2.5 E) Checking a Point Lies on a Line
We are able to check whether a point lies on a line by subbing in the x and y values from the coordinates that we are checking into the equation that we are given. If the equation holds (equals), then the point does lie on the line. If the equation does not hold, it means that the point does not lie on the line.
Example 1
We have a line with the equation y = 4x – 6. Point A has the coordinates (3, 7) and point B has the coordinates (1, -2); do they lie on the line?
Point A
Let’s check whether point A lies on the line first. Point A has the coordinates (3, 7). We check whether it lies on the line by subbing in x as 3 and y as 7. We then see whether the equation holds.
We have a line with the equation y = 4x – 6. Point A has the coordinates (3, 7) and point B has the coordinates (1, -2); do they lie on the line?
Point A
Let’s check whether point A lies on the line first. Point A has the coordinates (3, 7). We check whether it lies on the line by subbing in x as 3 and y as 7. We then see whether the equation holds.
This equation does not hold, which means that point A does not lie on the line.
Point B
Let’s now check whether point B lies on the line. Point B has the coordinates (1, -2), so we sub in x as 1 and y as -2.
Point B
Let’s now check whether point B lies on the line. Point B has the coordinates (1, -2), so we sub in x as 1 and y as -2.
The equation does hold, which means that point B does lie on the line.
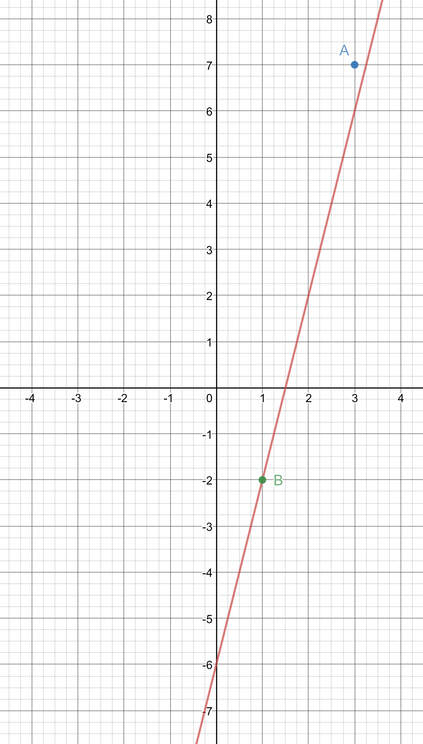
On the graph below, I have drawn the line (y = 4x – 6) and point A and Point B.
On the graph below, I have drawn the line (y = 4x – 6) and point A and Point B.
From the graph, we can see that point A does not lie on the line and point B does lie on the line.
End Note
Finding out whether a point does or does not lie on a line is fairly straightforward, but it is often something that students forget, so I think that it is worth making a revision card on how to check whether a point does or does not lie on a line.
Finding out whether a point does or does not lie on a line is fairly straightforward, but it is often something that students forget, so I think that it is worth making a revision card on how to check whether a point does or does not lie on a line.