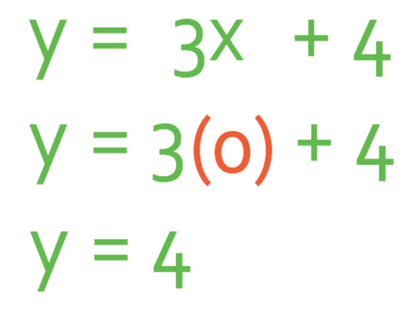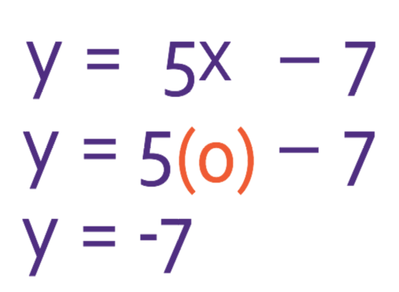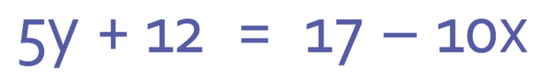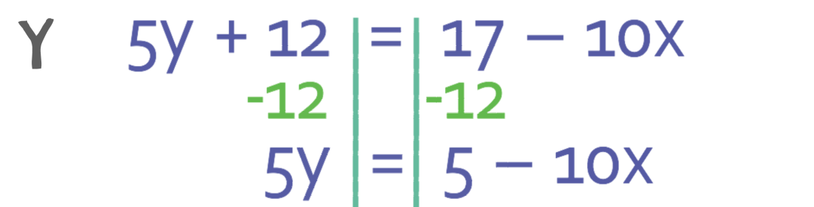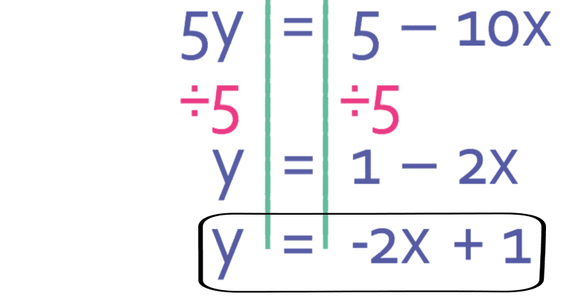Back to Edexcel Linear Graphs (H) Home
2.5 H) y Intercept
2.5 H) y Intercept
Usually linear lines are in the form of y = mx + c (or can be rearranged to take this form).
- m in this form refers to the gradient, which is the steepness of the line; a positive value for m means that the line is upwards sloping and a negative value for m means that the line is downwards sloping.
- c in the form is the y intercept and it is the value at which the line crosses the y axis. c is the y intercept because the x coordinate for any point on the y axis is 0. This means that when we sub x in as 0 into any line in the form y = mx + c, we are only left with c because m is multiplied by zero, which means that it disappears.
Example 1
Suppose that we have a line with the equation y = 3x + 4, what is the y intercept?
We can find the y intercept by subbing in x as 0 into the equation of the line.
Suppose that we have a line with the equation y = 3x + 4, what is the y intercept?
We can find the y intercept by subbing in x as 0 into the equation of the line.
Therefore, the coordinates for the y intercept is (0, 4). Alternatively, because the equation was in the form of y = mx + c, the y intercept would have been the value of c, which is 4, thus meaning the coordinates of the y intercept are (0, 4).
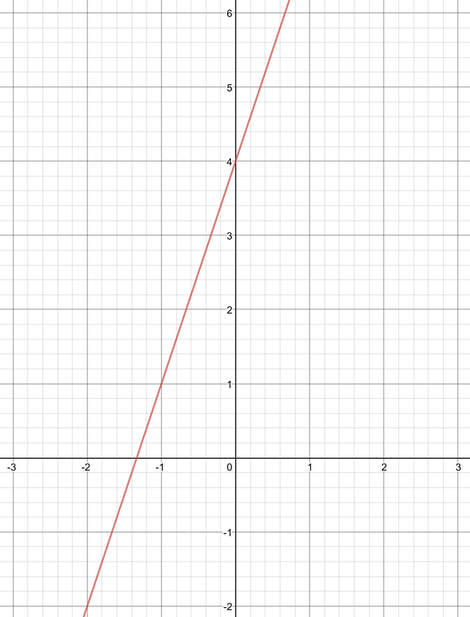
The line y = 3x + 4 is plotted on the graph below and from the sketch, you can see that the y intercept for the line is where y is 4, which has the coordinates (0, 4).
The line y = 3x + 4 is plotted on the graph below and from the sketch, you can see that the y intercept for the line is where y is 4, which has the coordinates (0, 4).
Changing the Value of c
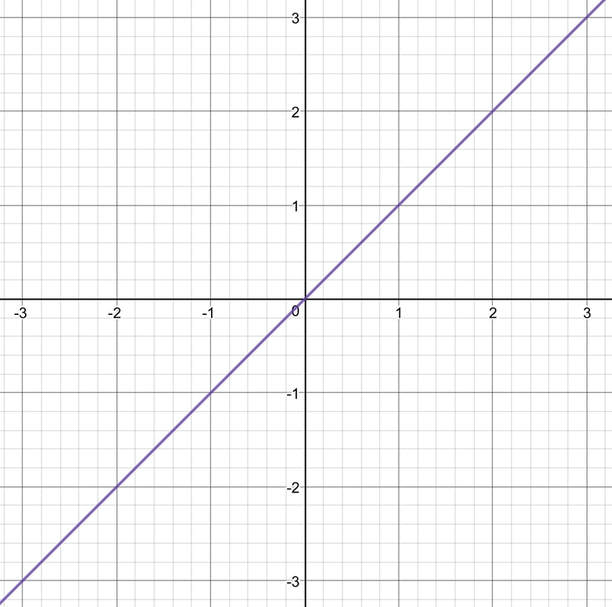
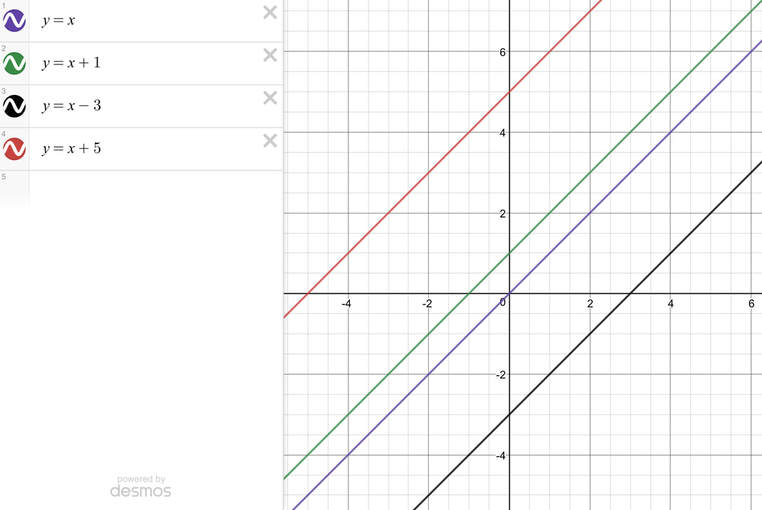
I am now going to have the line y = x and change the value for c. Currently, the value of c is zero and this means that the y intercept has the coordinates (0, 0); the graph passes through the origin. Below is a table working out the coordinates of the line y = x and a graph with y = x plotted.
I am now going to have the line y = x and change the value for c. Currently, the value of c is zero and this means that the y intercept has the coordinates (0, 0); the graph passes through the origin. Below is a table working out the coordinates of the line y = x and a graph with y = x plotted.
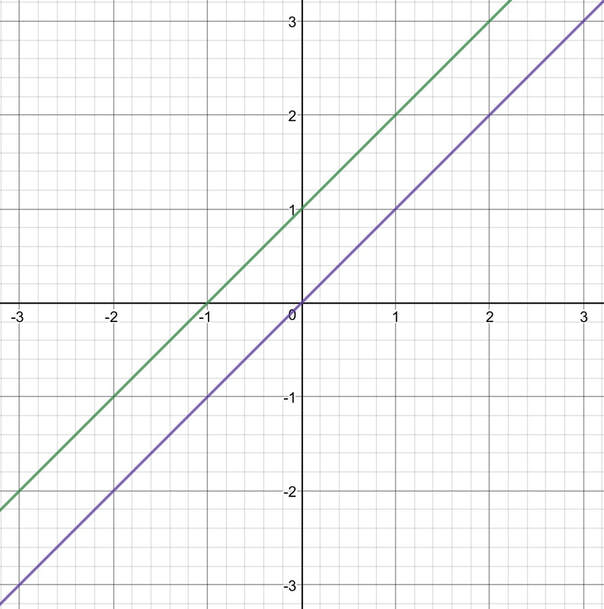
I am now going to change the value of c from 0 to 1. This results in the line becoming y = x + 1. The table and graph are shown below (the graph has the line y = x shown as well).
From the graph, we can see that all of the points on the line y = x have moved up by 1 to become the line y = x + 1. Also, the line y = x + 1 has a y value for the y intercept as 1 (the value of c) and the coordinates for the y intercept are (0, 1).
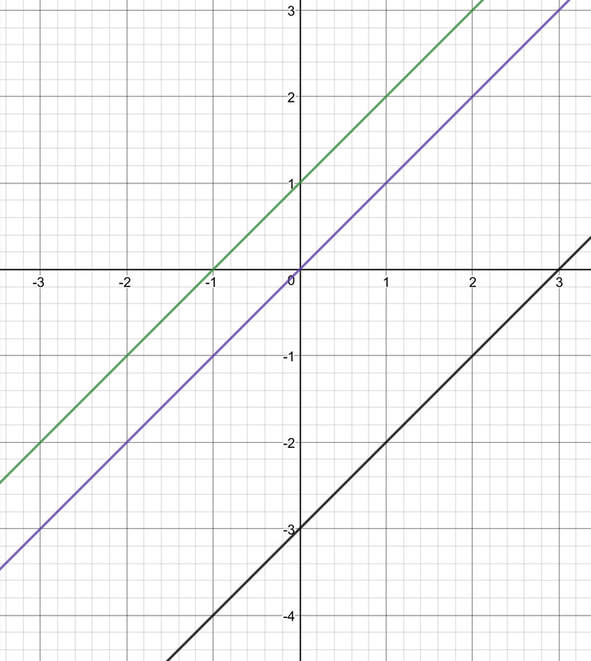
Let’s now plot the line y = x – 3. This line will intercept the y axis at -3 and it will have a gradient of 1. This means that we will move the line y = x down by 3. The line y = x – 3 is the black line on the graph below.
Let’s now plot the line y = x – 3. This line will intercept the y axis at -3 and it will have a gradient of 1. This means that we will move the line y = x down by 3. The line y = x – 3 is the black line on the graph below.
Finally, let’s plot the line of y = x + 5. The y intercept for this line is 5 (the value of c) and the gradient of the line is 1. Therefore, the line y = x will move up by 5.
Example 2
What are the coordinates for the y intercept for the line below?
What are the coordinates for the y intercept for the line below?
We can find the y value for the y intercept by subbing in x as 0.
The y value for the y intercept is -7 and the x value for the y intercept is 0. This means that the y intercept has the coordinates (0, -7).
Alternatively, because the line is already in the form of y = mx + c, the y intercept is going to be the value of c. For the line in this example, the value of c is -7, which means that the coordinates of the y intercept are (0, -7).
Alternatively, because the line is already in the form of y = mx + c, the y intercept is going to be the value of c. For the line in this example, the value of c is -7, which means that the coordinates of the y intercept are (0, -7).
Example 3
Find the gradient and y intercept of the line below. Also, roughly sketch what the line looks like.
Find the gradient and y intercept of the line below. Also, roughly sketch what the line looks like.
We are able to quickly find the gradient and y intercept of a line by getting the line into the form y = mx + c. Therefore, we need to rearrange the equation above and make y the subject. We do this by getting all of the y’s by their self on one side of the equation and all of the other terms on the other side of the equation. There are only y’s on the left and it makes sense to keep the y’s on this side. Therefore, we need to move the 12 from the left side of the equation to the right, which we are able to do by doing the opposite. The opposite of adding 12 is taking 12. Therefore, we take 12 from both sides of the equation.
We now have all of the y’s on one side of the equation and everything else on the other side. We want to have y is equal to something and not 5y is equal to something. Therefore, we need to divide both sides of the equation by 5.
We now have the equation in the y = mx + c form. The gradient of the line is -2 (the value for m), which means that the line is downwards sloping and fairly steep. The y value for the y intercept is 1 (the value for c), which means that the coordinates for the y intercept is (0, 1).
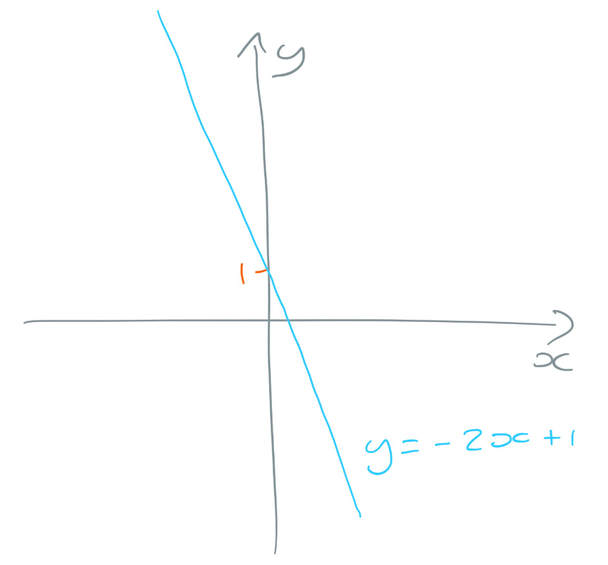
Below is a quick sketch of what this graph looks like.
Below is a quick sketch of what this graph looks like.