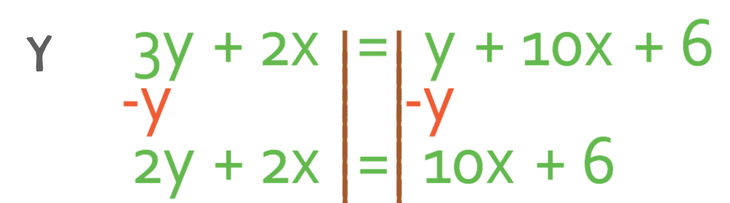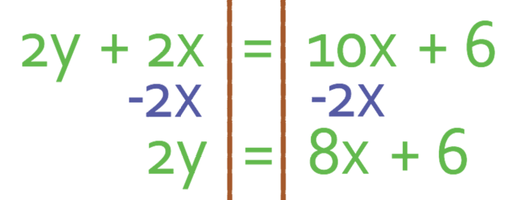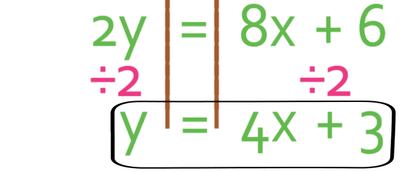Back to Edexcel Linear Graphs (H) Home
2.5 I) Parallel Lines
2.5 I) Parallel Lines
Parallel lines are lines that will never touch one another. The distance between parallel lines remains constant. Parallel lines have the same gradient, but they have different y intercepts; when the equations of the parallel lines are in the form of y = mx + c, the values for m will be the same and the values for c will be different.
The lines y = 3x + 1 and y = 3x – 2 are parallel. The gradient of both of these lines is 3 and the two lines have different values for c. These two lines are plotted below and from the graph, you can clearly see that the two lines are parallel.
The lines y = 3x + 1 and y = 3x – 2 are parallel. The gradient of both of these lines is 3 and the two lines have different values for c. These two lines are plotted below and from the graph, you can clearly see that the two lines are parallel.
Example 1
Are the two lines below parallel?
In order to say whether these two lines are parallel, we need to find what the gradient and y intercept are for the two lines. The easiest way to do this is to get the lines in the form y = mx + c.
Line 1 is already in this form and the gradient of line 1 is 4 (the value of m).
Line 2 is not in this form, but we can rearrange the equation to get it into this form by making y the subject. To make y the subject, we want to have all of the y’s on one side of the equation and all of the other terms on the other side of the equation. Currently, there are y’s on both sides of the equation. It is best to get all of the y’s to the side that currently has the greatest number of y’s. There are more y’s on the left side of the equation (3y is greater than y), so we get all of the y’s to the left and everything else to the right. This means that we need to get the y on the right to the left, which we do by taking y from both sides of the equation.
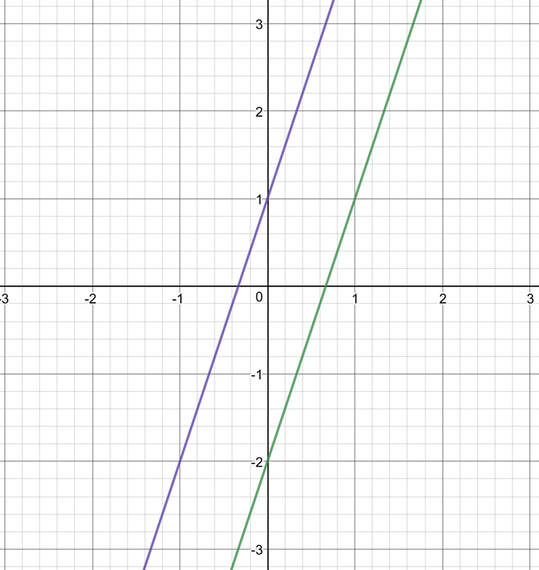
Are the two lines below parallel?
- Line 1: y = 4x + 2
- Line 2: 3y + 2x = y + 10x + 6
In order to say whether these two lines are parallel, we need to find what the gradient and y intercept are for the two lines. The easiest way to do this is to get the lines in the form y = mx + c.
Line 1 is already in this form and the gradient of line 1 is 4 (the value of m).
Line 2 is not in this form, but we can rearrange the equation to get it into this form by making y the subject. To make y the subject, we want to have all of the y’s on one side of the equation and all of the other terms on the other side of the equation. Currently, there are y’s on both sides of the equation. It is best to get all of the y’s to the side that currently has the greatest number of y’s. There are more y’s on the left side of the equation (3y is greater than y), so we get all of the y’s to the left and everything else to the right. This means that we need to get the y on the right to the left, which we do by taking y from both sides of the equation.
The next step is to move all of the non-y terms on the left to the right. This means that we move the 2x from the left side of the equation to the right. We are able to do this by doing the opposite and the opposite of adding 2x is taking 2x. Therefore, we take 2x from both sides of the equation.
We want to have y is equal to something and not 2y is equal to something. Therefore, we need to divide both sides of the equation by 2.
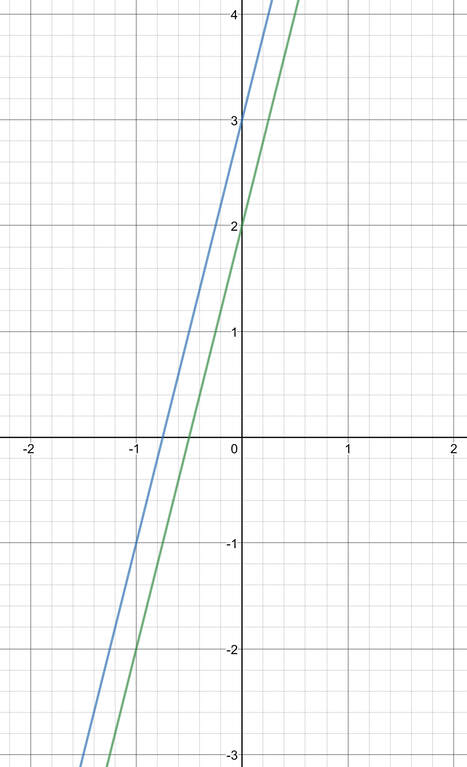
The line is now in the form of y = mx + c and this means that we can easily work out what the gradient of the line is. The gradient of line 2 is 4. This is the same gradient as line 1, which means that these two lines are parallel to one another. The two lines also have different values for c; the value for c in line 1 is 2 and the value for c in line 2 is 3.
The two lines are on the graph below. Line 1 is in green and line 2 is in blue.
The two lines are on the graph below. Line 1 is in green and line 2 is in blue.
Not Parallel
If two lines have different gradients, it means that the lines are not parallel to one another.
There are a few questions in the quiz that ask you to find out whether line are or are not parallel to one another.
If two lines have different gradients, it means that the lines are not parallel to one another.
There are a few questions in the quiz that ask you to find out whether line are or are not parallel to one another.