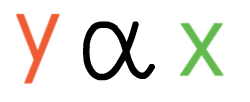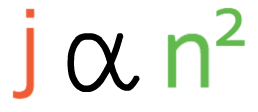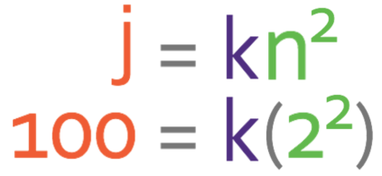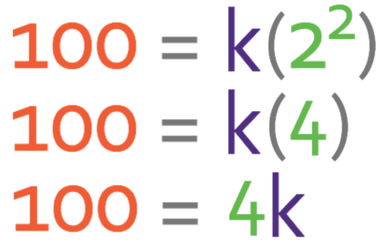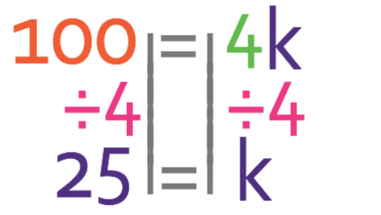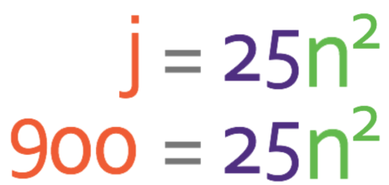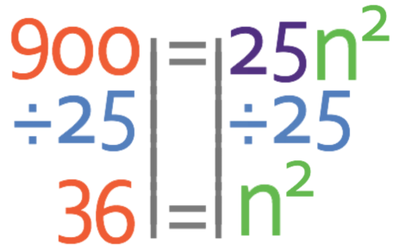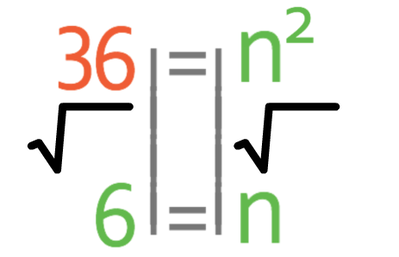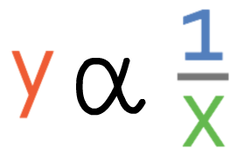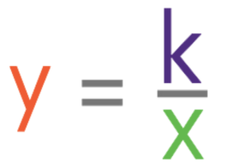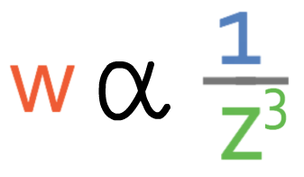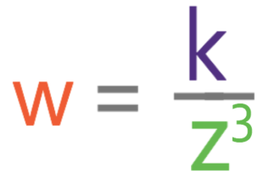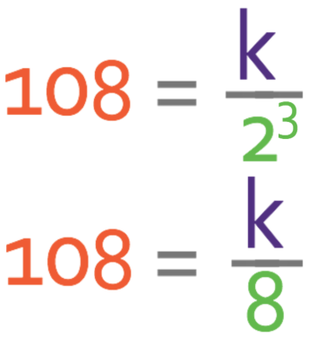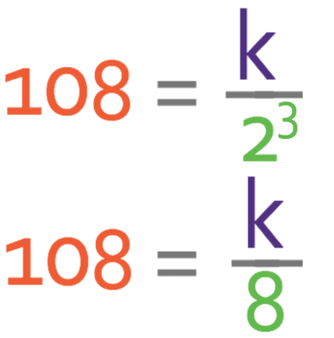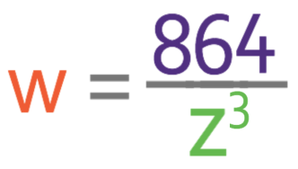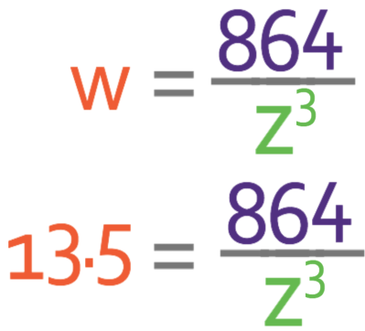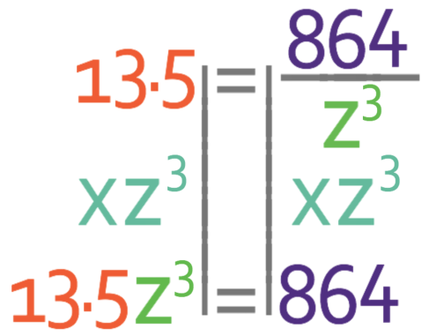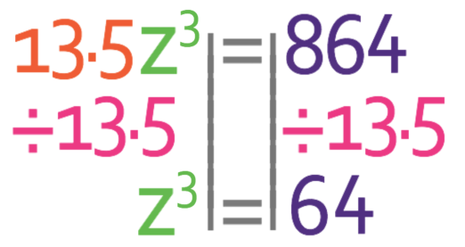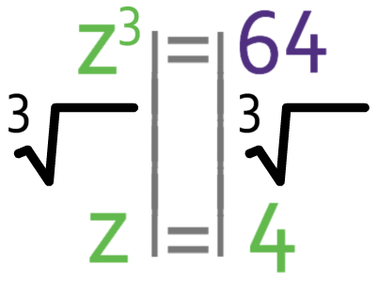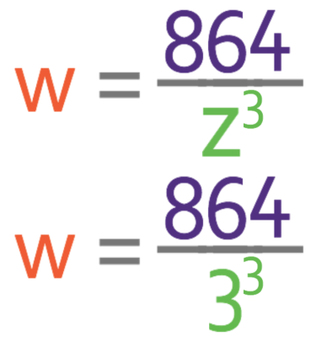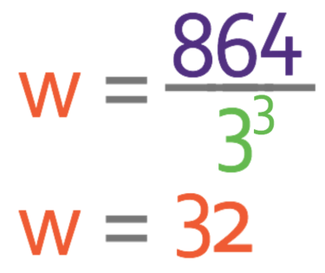Back to Edexcel Direct & Inverse Proportion (H) Home
​3.1 H) Direct & Inverse Proportion – Square or Cube
Sometimes it will be the case that you are given a variable that is directly or inversely proportional to the square, cube or root of another variable. The notation and process to answer these types of questions is pretty much exactly the same as the previous examples that we have looked at, the only difference is that we replace one of the variables with the square, cube or root of the other variable. We will be looking at two examples in this section; the first example is one that is “directly proportional to a square” and the second example is one that is “inversely proportional to the cube”.
Example 1 – Direct Proportion to the Square
If we had two variables (x & y) that were in direct proportion to one another, the notation and the general equation would be:
Direct proportion notation
Direct proportion general equation
​If we were now told that we had two different variables (j & n) and j was directly proportional to the square of n, we would change our notation and the general equation to become:
Direct proportion to a square notation
Direct proportion to a square general equation
Let’s expand on this example with some values. When j is 100, n is 2. Also, both variables are always positive.
a) Form an equation for j in terms of n.
b) Find the value of j when n is 3.
c) Find the value of n when j is 900.
 
Part a
Part a asks us to form an equation for j in terms on n. The general equation for this question is:
In order to form an equation, we need to find the value of k. We are able to find the value of k by subbing in the pair of values for j and n that we were given in the question. We were told in the question that when j is 100, n is 2. Therefore, we sub in j as 100 and n as 2 into the general equation.
According to BODMAS/BIDMAS, we need to square the 2 first.
We want to find the value of k and not 4k. Therefore, we divide both sides of the equation by 4.
This tell us that k is 25. We can replace k with 25 in the general equation. The general equation becomes:
We now have an equation for j in terms of n. This equation is useful because we can sub in any value for j or n to find the value of the other variable.
 
Part b
Part b asks us to find the value of j when n is 3. We do this by subbing n as 3 into the general equation.
This tells us that when n is 3, j is 225.
 
Part c
Part c asks us to find the value of n is when j is 900. We do this by subbing in j as 900 into the general equation.

We want to find the value of n (make n the subject). The first step to achieve this is to get n2 by itself. At the moment, we have 25n2 and we are able to get just n2 by dividing both sides of the equation by 25.

We want to find the value of n and not n2. Therefore, we need to square root both sides of the equation.

​Whenever we square root something, we get a positive and a negative answer. The square root of 36 is ±6 (6 and -6). However, we were told in the question that both of the variables are always positive, and this means that we ignore the negative answer, thus meaning that the answer for n is 6.
 
Therefore, when j is 900, n is 6.
Example 2 – Inverse Proportional to the Cube
Let’s remind ourselves of the notation and general formula for inverse proportion. If y was inversely proportional to x, the notation and general formula would be:
Inverse proportion notation
Inverse proportion general equation

Let’s now have an example. w is inversely proportional to z3. When w is 108, z is 2.

a) Form an equation for w in terms of z.

b) Find the value of z when w is 13.5.

c) Find the value of w when z is 3.

 

Part a

The question tells us that w is inversely proportional to z3. The notation and general equation for this would be:

Inverse proportion to a cube notation
Inverse proportion to a cube general equation
In order to form an equation, we need to find the value of k. We find the value of k by subbing in the values for w and z that we were given in the question. We were told in the question that when w is 108, z is 2. Therefore, we sub w in as 108 and z in as 2.
​According to BODMAS/BIDMAS, we need to cube the 2 first.
We want to find the value of k and not k divided by 8 (the dividing by 8 is coming from the denominator of the fraction). We are able to get rid of the divided by 8 by doing the opposite; the opposite of dividing by 8 is multiplying by 8. Therefore, we multiply both sides of the equation by 8.
This tells us that k is 864. We replace k in the general equation with 864. The general equation becomes:
We now formed an equation for w in terms of z, which answers part a and will help us to answer part b and c.
 
Part b
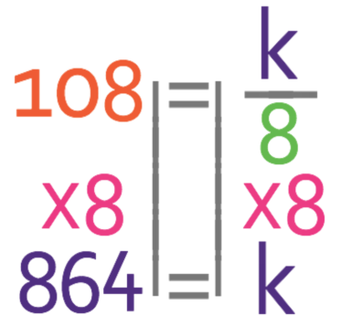
Part b asks us to find the value of z when w is 13.5. We are able to do this by subbing in w as 13.5 into the general equation.

We want to find the value of z. Currently we have z3 on the denominator of a fraction, which is far from ideal. Therefore, the first step should be to bring the z3 up from the denominator of the fraction/ get rid of the denominator. We are able to do this by multiplying both sides of the equation by z3 (we get rid of the denominator of a fraction in an equation by multiplying both sides of the equation by the denominator).

The next step in finding the value of z is to get z3 by itself. Currently we have 13.5z3. We can get just z3 by dividing both sides of the equation by 13.5.

We want to find the value of z and not z3. Therefore, we cube root both sides of the equation.

Therefore, when w is 13.5, z is 4.
 
Part c
Part c asks us to find the value of w when z is 3. We are able to do this by subbing in z as 3 into the general equation.
We can type the fraction on the right side of the equation into a calculator.
Therefore, when z is 3, w is 32.
End Note
Direct and inverse proportion questions involving squares, cubes and roots are not too dissimilar to the normal direct and inverse proportion questions. The only difference is that a square, cube or root is involved, and this results in there being some more steps in the working. Providing you are carful with these types of questions, you should find them ok after you have tried a few questions. There are quite a few questions like this in the quiz, so it is definitely worth giving the quiz a go.