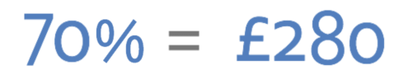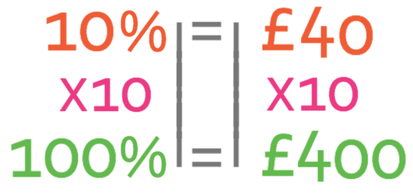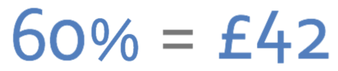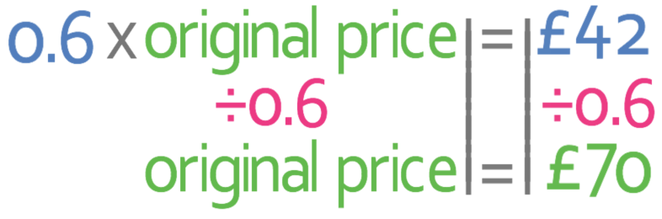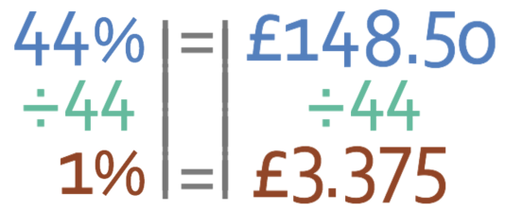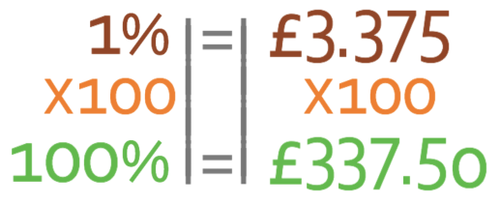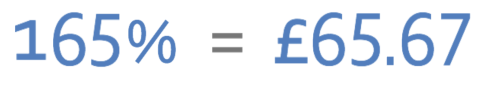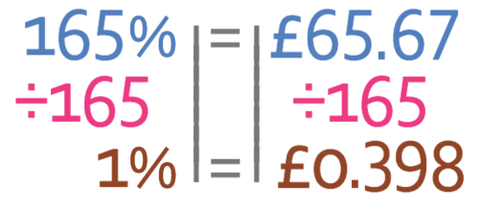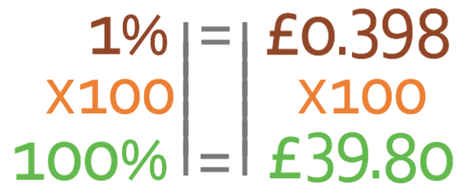Back to Edexcel Percentages (H) Home
3.2 L) Reverse Percentages
3.2 L) Reverse Percentages
Reverse percentages are very useful at working out the original value after a value has been increased or decreased by a certain percentage. For example, we can use reverse percentages to work out what the price of a good was before it was placed into a sale. Let’s have an example.
Example 1
I go to the sales to buy a phone. The phone is in the sale and has 30% off. The price of the phone in the sale is £280. What was the initial price of the phone? Do not use a calculator.
We are asked to work out the initial price of the phone. This price represents 100% of the price of the phone. In the sale, the phone has had 30% taken off it. This means that the price of the phone in the sale represents 70% of the initial price of the phone.
I go to the sales to buy a phone. The phone is in the sale and has 30% off. The price of the phone in the sale is £280. What was the initial price of the phone? Do not use a calculator.
We are asked to work out the initial price of the phone. This price represents 100% of the price of the phone. In the sale, the phone has had 30% taken off it. This means that the price of the phone in the sale represents 70% of the initial price of the phone.
From this information, we are able to create the following equation.
We want to find out what the initial/ non-sale price of the phone and this represents 100%. The easiest way to find 100% is to find what 10% is, and then multiply by 10 to find what 100% is.
The percentage in the above equation is 70%. We can find what 10% is by dividing both sides of the equation by 7.
The percentage in the above equation is 70%. We can find what 10% is by dividing both sides of the equation by 7.
We want to find what 100% is and not 10%. Therefore, we multiply both sides of the equation by 10.
The non-sale/ initial price of the phone is £400. After we have obtained our answer, it is a good idea to check whether it makes sense. The initial price was £400, and this is greater than the sale price of the phone (£280), thus implying that we have the correct values.
Alternative Method
I am going to use a calculator for this method.
An alternative method is to use the multiplier method to create an equation. The phone in the sale is 70% of what it was non-sale. 70% as a decimal is 0.7 (remember to convert percentages into decimals, we divide by 100). Therefore, 0.7 multiplied by the original price will be the sale price. This gives us the equation below.
Alternative Method
I am going to use a calculator for this method.
An alternative method is to use the multiplier method to create an equation. The phone in the sale is 70% of what it was non-sale. 70% as a decimal is 0.7 (remember to convert percentages into decimals, we divide by 100). Therefore, 0.7 multiplied by the original price will be the sale price. This gives us the equation below.
We want to find the original price and not 0.7 of the original price. Therefore, we divide both sides of the equation by 0.7.
This gives us the same answer as we got before, which is an original price of £400. (note: when we divide by a positive number that is less than 1, the answer will be greater than the number that we start with).
Example 2
A coat in the sale has 40% off of it. The sale price of the coat is £42. What is the original (non-sale) price of the coat?
We are asked to find the price of the coat and the original price is 100%. The coat in the sale has 40% off and this means that the sale price of the coat (£42) is 60% of the full price of the coat.
A coat in the sale has 40% off of it. The sale price of the coat is £42. What is the original (non-sale) price of the coat?
We are asked to find the price of the coat and the original price is 100%. The coat in the sale has 40% off and this means that the sale price of the coat (£42) is 60% of the full price of the coat.
We are told in the question that the sale price of the coat is £42 and this represents 60%. We can create the following equation from this information:
The non-sale price of the coat is 100%. The easiest way to find 100% from 60% is to find what 10% is and then what 100% is.
We are able to find what 10% is from 60% by dividing both sides of the equation by 6.
We are able to find what 10% is from 60% by dividing both sides of the equation by 6.
We want to find 100% and not 10%. Therefore, we need to multiply both sides of the equation by 10.
Therefore, the original price of the coat is £70.
Alternative method
I am now going to answer this question using the alternative method. The coat in the sale is 60% of the full price. 60% as a multiplier is 0.6 (60 ÷ 100 = 0.6). Therefore, 0.6 multiplied by the original price is the sale price. This gives the equation that is shown below:
Alternative method
I am now going to answer this question using the alternative method. The coat in the sale is 60% of the full price. 60% as a multiplier is 0.6 (60 ÷ 100 = 0.6). Therefore, 0.6 multiplied by the original price is the sale price. This gives the equation that is shown below:
We want to find the original price and not 0.6 of the original price. Therefore, we divide both sides of the equation by 0.6.
The original price of the coat is £70.
Example 3
Let’s have another example where we have a discounted item. I book a last-minute holiday to Berlin. The holiday has 56% off. I pay £148.50 for the holiday. How much was the holiday when it was not in the sale? You may use a calculator.
We are told that I pay £148.50 for the holiday and the price that I pay is 56% less than the price when the holiday was at full price. From this information, I can work out what percentage of the original holiday I am paying. The original price of holiday represents 100% of the original price and I am getting a discount of 56%. Therefore, I am paying 44% of the price of the original holiday.
Let’s have another example where we have a discounted item. I book a last-minute holiday to Berlin. The holiday has 56% off. I pay £148.50 for the holiday. How much was the holiday when it was not in the sale? You may use a calculator.
We are told that I pay £148.50 for the holiday and the price that I pay is 56% less than the price when the holiday was at full price. From this information, I can work out what percentage of the original holiday I am paying. The original price of holiday represents 100% of the original price and I am getting a discount of 56%. Therefore, I am paying 44% of the price of the original holiday.
We know that this 44% is equal to the amount that I paid for the holiday.
Now, let’s find out what 1 percentage point of the holiday is. We do this by dividing both sides by 44.
The non-sale price of the holiday is 100%, so we need to multiply both sides by 100.
Therefore, the original price of the holiday is £337.50.
Alternative Method
I will now work through this example using the other algebraic framework. We know that the price that I paid for my holiday is 44% of what the original/ non-sale price of the holiday was. We can convert 44% into a decimal by dividing by 100, which gives us a decimal of 0.44. Therefore, we have the following algebraic equation.
Alternative Method
I will now work through this example using the other algebraic framework. We know that the price that I paid for my holiday is 44% of what the original/ non-sale price of the holiday was. We can convert 44% into a decimal by dividing by 100, which gives us a decimal of 0.44. Therefore, we have the following algebraic equation.
We want to find the value for the original price, so we divide both sides by 0.44.
The original price of the holiday is £337.50, which is the same value that we obtained earlier.
Example 4
I want to go to a concert, but unfortunately, I missed out on purchasing a ticket, which means that I need to purchase a ticket off a secondary selling site. The price of the ticket is £65.67 on the secondary selling site, which is 65% more expensive than the original ticket. How much was the original ticket if I had purchased it from the original seller’s site and not from the secondary ticket selling site? You may use a calculator.
Like in the examples above, the original ticket price represents 100%. The ticket that I purchase off the secondary selling site is 65% more expensive than the original selling price. As it is 65% more expensive, it means that we add the percentage that it is more expensive by onto the 100% (before, the prices were decreased by a percentage, which meant that we took the percentage that they were cheaper by off of 100%).
I want to go to a concert, but unfortunately, I missed out on purchasing a ticket, which means that I need to purchase a ticket off a secondary selling site. The price of the ticket is £65.67 on the secondary selling site, which is 65% more expensive than the original ticket. How much was the original ticket if I had purchased it from the original seller’s site and not from the secondary ticket selling site? You may use a calculator.
Like in the examples above, the original ticket price represents 100%. The ticket that I purchase off the secondary selling site is 65% more expensive than the original selling price. As it is 65% more expensive, it means that we add the percentage that it is more expensive by onto the 100% (before, the prices were decreased by a percentage, which meant that we took the percentage that they were cheaper by off of 100%).
This means that the price of the ticket on the secondary seller’s site is 165% of the price of the ticket if it was to have been purchased from the initial site. We can now equal this percentage to the price that I paid for the tickets.
We want to know what 100% is. To get 100%, we first need to find what 1% is. We find what 1% is by dividing both sides of the equation by 165.
We find 100% by multiplying both sides by 100.
Therefore, the original price of the ticket was £39.80. This price makes sense because it is less than the price of the ticket on the secondary selling site and we are told in the question that the secondary selling site is more expensive than the original price of the ticket.
Alternative Method
Now let’s use the other algebraic framework. We have already established that the final price of the ticket is 165% of the initial price of the ticket. We are now going to convert 165% into a decimal, which we do by dividing by 100. 165% as a decimal is 1.65. Therefore, we have the following algebraic equation.
Alternative Method
Now let’s use the other algebraic framework. We have already established that the final price of the ticket is 165% of the initial price of the ticket. We are now going to convert 165% into a decimal, which we do by dividing by 100. 165% as a decimal is 1.65. Therefore, we have the following algebraic equation.
We want to know what the “original price” of the ticket is and we want to make that the subject. We make the “original price” the subject by dividing both sides by 1.65.
The original price of the ticket is £39.80, which is exactly the same price we found when we were using the previous method.