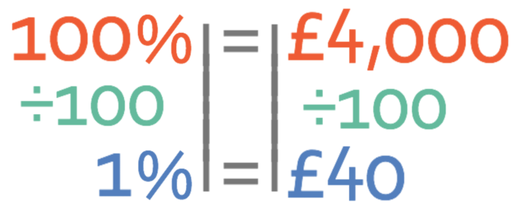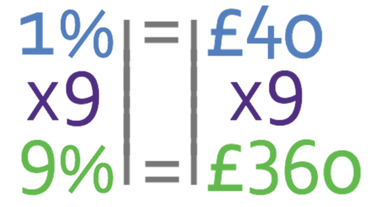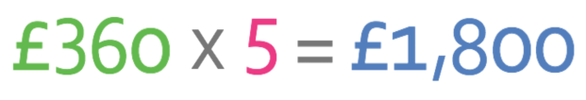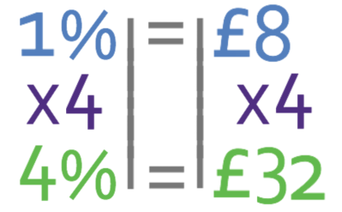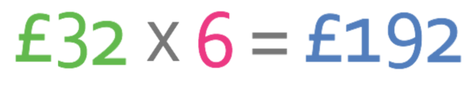Back to Edexcel Percentages (H) Home
3.2 M) Simple Interest
3.2 M) Simple Interest
There are two different types of interest that we look at in maths. These are simple interest and compound interest. We will look at simple interest in this section and compound interest in the next sections.
Simple Interest
With simple interest, the interest earnt per year is the same every year; the interest earnt in the first year will be the same as the interest earnt in the fifth year, ninth year, twentieth year etc…
With simple interest, the interest earnt per year is the same every year; the interest earnt in the first year will be the same as the interest earnt in the fifth year, ninth year, twentieth year etc…
Example 1
I place £4000 in a bank account that gives 9% simple interest per year for 5 years. How much interest will I have earnt after 5 years?
This is simple interest, which means that the interest earnt per year will be the same every year; the interest earnt in year 1 will be the same as the interest earnt in year 2, year 3, year 4 and year 5. Therefore, we work out the total interest earnt by working out the interest earnt in one year, and then we multiply it by the number of years (which for this question is 5).
We are able to work out the interest earnt in one year by using two different methods; working out 1% or by using the multiplier method.
Method 1: Finding 1%
This method involves finding 1% and multiplying 1% by the amount of percent that we need. To find 1%, we divide the amount of money (£4000) by 100.
I place £4000 in a bank account that gives 9% simple interest per year for 5 years. How much interest will I have earnt after 5 years?
This is simple interest, which means that the interest earnt per year will be the same every year; the interest earnt in year 1 will be the same as the interest earnt in year 2, year 3, year 4 and year 5. Therefore, we work out the total interest earnt by working out the interest earnt in one year, and then we multiply it by the number of years (which for this question is 5).
We are able to work out the interest earnt in one year by using two different methods; working out 1% or by using the multiplier method.
Method 1: Finding 1%
This method involves finding 1% and multiplying 1% by the amount of percent that we need. To find 1%, we divide the amount of money (£4000) by 100.
This tells us that 1% is £40. We want 9%, which means that we multiply our value for 1% by 9.
Method 2: Using a Multiplier
This method involves turning 9% into a multiplier (a decimal) and multiplying the multiplier by the amount of money saved.
9% as a multiplier is 0.09 (9 ÷ 100 = 0.09). The next step is to multiply 0.09 by the amount that was saved.
This method involves turning 9% into a multiplier (a decimal) and multiplying the multiplier by the amount of money saved.
9% as a multiplier is 0.09 (9 ÷ 100 = 0.09). The next step is to multiply 0.09 by the amount that was saved.
The interest earnt per year is £360, which is the same value as the previous method.
The multiplier method is quicker at finding the interest, but it is slightly more complex. Therefore, you should use the method that you feel more comfortable with.
Back to the Question
With simple interest, the amount of interest is the same for every year; the amount of interest is the same in year 1, year 2, year 3, year 4 and year 5. Therefore, we work out the total amount of interest earnt by multiplying the amount of interest earnt in one year (£360) by the number of years that the money was kept in the bank for (5).
The multiplier method is quicker at finding the interest, but it is slightly more complex. Therefore, you should use the method that you feel more comfortable with.
Back to the Question
With simple interest, the amount of interest is the same for every year; the amount of interest is the same in year 1, year 2, year 3, year 4 and year 5. Therefore, we work out the total amount of interest earnt by multiplying the amount of interest earnt in one year (£360) by the number of years that the money was kept in the bank for (5).
Therefore, the amount of interest that was earnt after 5 years was £1,800.
Example 2
I put £800 into a savings account that pays 4% simple interest per year. How much money will I have in my bank account after 6 years?
This is another simple interest question, which means that the interest that is paid per year will be the same for all of the years; the interest paid in the first year will be the same as the interest paid in the sixth year. We work out the total amount of interest earnt by finding the interest earnt in one year, and then we multiply this amount by the number of years that the money is kept in the bank (6 years).
The question tells us that the interest rate is 4% and the amount of money in the bank account is £800. From this information, we are able to work out the amount of interest earnt per year. Like the previous question, we can do this in two different ways.
Method 1: Finding 1%
This method involves finding 1% and multiplying 1% by the amount of percent that we need. To find 1%, we divide the amount of money (£800) by 100.
I put £800 into a savings account that pays 4% simple interest per year. How much money will I have in my bank account after 6 years?
This is another simple interest question, which means that the interest that is paid per year will be the same for all of the years; the interest paid in the first year will be the same as the interest paid in the sixth year. We work out the total amount of interest earnt by finding the interest earnt in one year, and then we multiply this amount by the number of years that the money is kept in the bank (6 years).
The question tells us that the interest rate is 4% and the amount of money in the bank account is £800. From this information, we are able to work out the amount of interest earnt per year. Like the previous question, we can do this in two different ways.
Method 1: Finding 1%
This method involves finding 1% and multiplying 1% by the amount of percent that we need. To find 1%, we divide the amount of money (£800) by 100.
This tells us that 1% is £8. We want 4%, which means that we multiply our value for 1% by 4:
The interest earnt per year is £32.
Method 2: Using a Multiplier
This method involves turning 4% into a multiplier (a decimal) and multiplying the multiplier by the amount of money saved.
4% as a multiplier is 0.04 (4 ÷ 100 = 0.04). The next step is to multiply 0.04 by the amount that was saved.
Method 2: Using a Multiplier
This method involves turning 4% into a multiplier (a decimal) and multiplying the multiplier by the amount of money saved.
4% as a multiplier is 0.04 (4 ÷ 100 = 0.04). The next step is to multiply 0.04 by the amount that was saved.
The interest earnt per year is £32, which is the same value as the previous method.
Back to the Question
We now know that the amount of interest per year is £32 and this will be the same for all years. The question tells us that our individual keeps their money in the bank for 6 years. Therefore, we can work out the total interest by multiplying the interest per year (£32) by the number of years that the money is kept in the bank (6).
Back to the Question
We now know that the amount of interest per year is £32 and this will be the same for all years. The question tells us that our individual keeps their money in the bank for 6 years. Therefore, we can work out the total interest by multiplying the interest per year (£32) by the number of years that the money is kept in the bank (6).
The total amount of interest that our individual earns is £192.
The question asks us to work out the amount of money that our individual has in the bank after the 6 years. We are able to work this out by adding the total amount of interest earnt (£192) to the amount of money that was in the bank (£800).
The question asks us to work out the amount of money that our individual has in the bank after the 6 years. We are able to work this out by adding the total amount of interest earnt (£192) to the amount of money that was in the bank (£800).
Therefore, at the end of the 6 years, our individual has £992 in their bank account.
Final Note
The key rule to remember with simple interest is that the amount of interest is the same EVERY year; the amount of interest will be the same in the first year, fifth year, twentieth year etc…. Therefore, we answer simple interest questions by working out the interest earnt in one year. We then multiply the interest earnt in one year by the number of years that the money is kept in the bank for.
Also, when answering simple interest questions, make sure that you read the question carefully to check whether you are asked to find the amount of interest earnt (question 1) or the amount of money in the bank account (question 2).
The key rule to remember with simple interest is that the amount of interest is the same EVERY year; the amount of interest will be the same in the first year, fifth year, twentieth year etc…. Therefore, we answer simple interest questions by working out the interest earnt in one year. We then multiply the interest earnt in one year by the number of years that the money is kept in the bank for.
Also, when answering simple interest questions, make sure that you read the question carefully to check whether you are asked to find the amount of interest earnt (question 1) or the amount of money in the bank account (question 2).