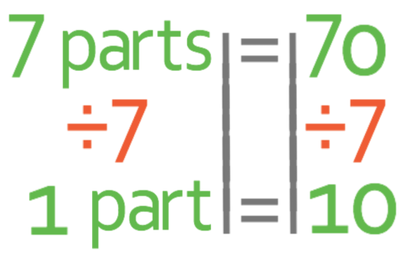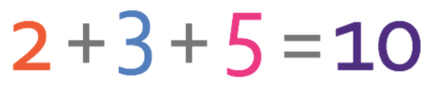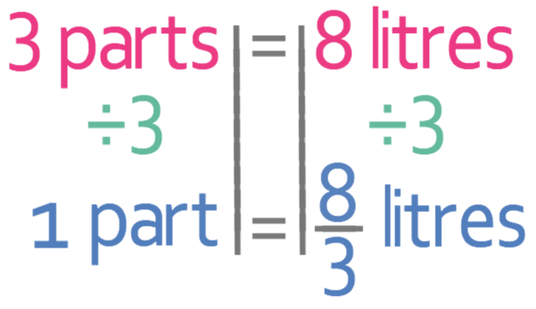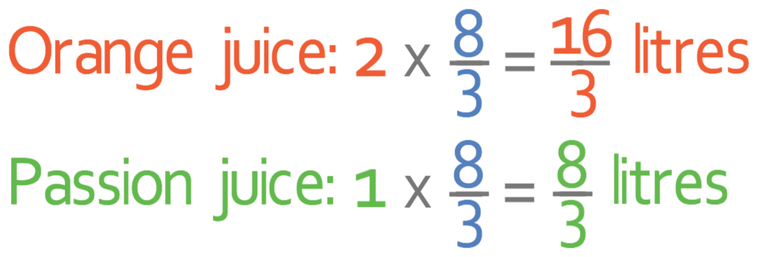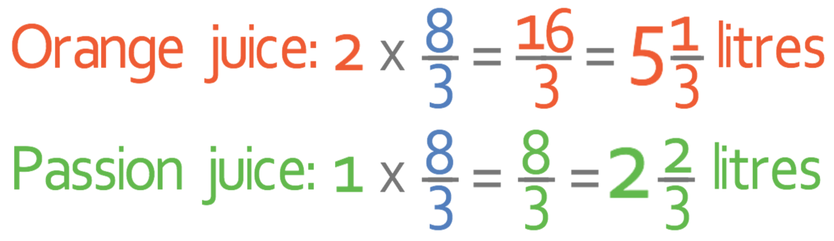Back to Edexcel Ratio (H) Home
3.3 E) Sharing Through a Ratio
3.3 E) Sharing Through a Ratio
Ratios are very useful at sharing different amounts. We use ratio in liquids (making squash or a cleaning solution), when we are sharing money or sweets and many more real-world examples.
Example 1
We have 70 sweets and they are given to John and Karen in the ratio 4 : 3. How many sweets do John and Karen get each?
We have 70 sweets and they are given to John and Karen in the ratio 4 : 3. How many sweets do John and Karen get each?
The first step to answering this question is to add the two numbers in the ratio together to give us the number of parts in the ratio.
The 7 parts in this ratio represent the total number of sweets that are being shared. Therefore, we have the equation:
The next step is to find how many sweets 1 part represents. At the moment, we have 7 parts and we are able to find what 1 part is by dividing both sides by 7.
This tells us that 1 part in the ratio is equal to 10 sweets. We are now able to work out how many sweets John and Karen get.
John has 4 parts and we work out the number of sweets that he gets by multiplying the number of parts that he has (4) by the number of sweets that 1 part represents (10).
John has 4 parts and we work out the number of sweets that he gets by multiplying the number of parts that he has (4) by the number of sweets that 1 part represents (10).
There is a similar process for Karen; she has 3 parts.
From our calculation, we have found that John gets 40 sweets and Karen gets 30 sweets. It is always a good idea to check whether the 70 sweets have actually been split up between John and Karen. We can do this by adding the number of sweets that John gets (40) and the number of sweets that Karen gets (30). This gives us 70, which is the number of sweets that are being shared, thus implying that we have the correct answer.
Example 2
£40 is shared between Steph, Suzie and Olivia in the ratio 2 : 3 : 5. How much money do they each get?
£40 is shared between Steph, Suzie and Olivia in the ratio 2 : 3 : 5. How much money do they each get?
The first step in answering this question is to find the total number of parts in the ratio. We do this by adding all of the components in the ratio together.
These 10 parts in the ratio represent the total money that is shared, which is £40. This gives us the equation that is shown below:
The next step is to work out what 1 part in the ratio represents. We do this by dividing both sides of the above equation by 10.
We now need to find out how much money each individual gets. We do this by multiplying the number of parts that they have in the ratio by what 1 part represents (which is £4).
Let’s start by finding out how much Steph gets. To find out how much Steph gets, we multiply the number of parts that she has (2) by what 1 part represents (£4).
Let’s start by finding out how much Steph gets. To find out how much Steph gets, we multiply the number of parts that she has (2) by what 1 part represents (£4).
We do the same for Suzie and Olivia. Suzie has 3 parts and Olivia has 5 parts.
Therefore, Steph gets £8, Suzie gets £12 and Olivia gets £20. It is a good idea to check that the amount of money that they each get adds up to amount of money that was shared out. In this example, £40 was shared out and the amount that they each got does add up to £40 (£8 + £12 + £20 = £40).
Example 3
The ratio of orange juice to passion fruit juice in orange and passion juice is 2:1. How much orange juice and passionfruit juice is needed to make 8 litres of orange and passion fruit juice?
The ratio of orange juice to passion fruit juice in orange and passion juice is 2:1. How much orange juice and passionfruit juice is needed to make 8 litres of orange and passion fruit juice?
We use the same method to answer this question as we did for the question above. The first step is to work out how many parts we have, and we have 3 parts (2 + 1 = 3).
We want to find what 1 part represents. We do this by dividing both sides of the equation by 3.
1 part of the ratio represents 8/3 litres. We now need to find out how much orange juice and passion fruit juice we need. We do this by multiplying the number of parts for each of the fruit juices by what 1 part of the ratio represents (which is 8/3 litres). Orange juice in the ratio is 2 parts and passion fruit juice is 1 part.
Both of the fractions that we have are improper. This is because the numerator (the number at the top of the fraction) is greater than the denominator (the number at the bottom of the fraction). We are able to convert improper fractions into mixed numbers by seeing how many wholes there are in the fraction. We do this by dividing the numerator by the denominator. The remainder of the division will be the numerator of the fraction that will be next to the whole number (the denominator of the fraction next to the whole number will be the same as it was before). More information about mixed number and improper fractions can be found in the fraction section.