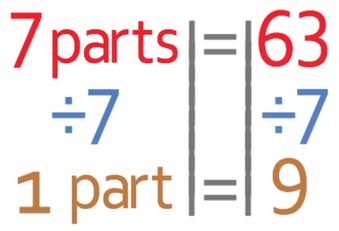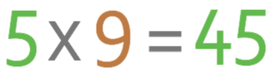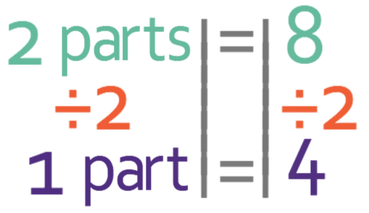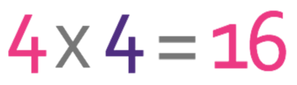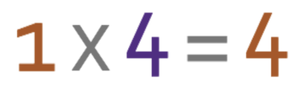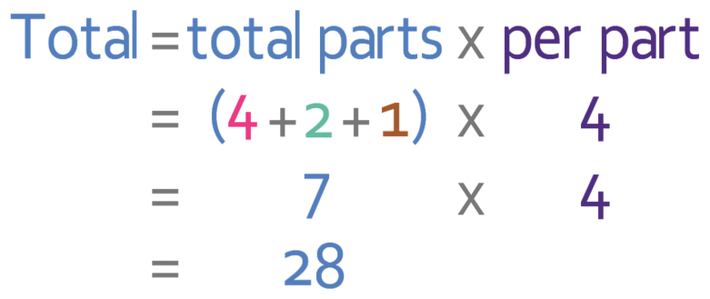Back to Edexcel Ratio (H) Home
3.3 F) Finding Unknowns in a Ratio
3.3 F) Finding Unknowns in a Ratio
Sometimes you may be given a ratio and told the number of what one of the components in the ratio represents. You may then be asked to work out what the other components in the ratio represents, or what all of the components represent (the total). The best way to learn how to answer these types of questions is to go through examples. There are 2 examples in this section.
Example 1
The ratio of red sweets to green sweets is 7:5. There are 63 red sweets. How many green sweets are there and how many sweets are there in total?
The ratio of red sweets to green sweets is 7:5. There are 63 red sweets. How many green sweets are there and how many sweets are there in total?
Let’s find out how many green sweets there are first. In the question, we are told that there are 63 red sweets and these red sweets equal 7 parts in the ratio. This gives us the following equation:
We are able to find out what 1 part represents by dividing both sides by 7.
We now know that 1 part of the ratio represents 9 sweets. As we know what 1 part is, we are now able to work out how many green sweets there are. We are told in the question that 5 parts of the ratio are red sweets and each part represents 9 sweets. To work out how many green sweets there are, we multiply the number of parts (5) by what 1 part represents (9).
This tells us that there are 45 green sweets.
The second part of the question asks us to work out how many sweets there are in total. We can work this out in two ways.
The first way is to add the number of red sweets to the number of green sweets. The number of red sweets is given in the question (63) and we have just worked out the number of green sweets (45). Therefore, the total number of sweets is 108.
The second method for working this out is to multiply the total number of parts in the ratio (12) by what one part represents (9). This gives us 108 sweets, which is the same answer that we had before. The working for this method is shown below.
The second part of the question asks us to work out how many sweets there are in total. We can work this out in two ways.
The first way is to add the number of red sweets to the number of green sweets. The number of red sweets is given in the question (63) and we have just worked out the number of green sweets (45). Therefore, the total number of sweets is 108.
The second method for working this out is to multiply the total number of parts in the ratio (12) by what one part represents (9). This gives us 108 sweets, which is the same answer that we had before. The working for this method is shown below.
Example 1
An orchestra has many instruments in it. The ratio of violinists to cellists to double bassists is 4 : 2 : 1. There are 8 cellists in the band. How many violinists and double bassists are there in the band and how many members are in the band in total?
An orchestra has many instruments in it. The ratio of violinists to cellists to double bassists is 4 : 2 : 1. There are 8 cellists in the band. How many violinists and double bassists are there in the band and how many members are in the band in total?
We answer this question by working out how much 1 part represents. The question tells us that there are 8 cellists in the band and these cellists represents two parts in the ratio. We can create the equation below from this information.
We are able to find what 1 part is by dividing both sides of the equation by 2.
Therefore, 1 part in the ratio represents 4 players. We are now able to work out the number of violinists and double bassists.
Violinists
4 parts in the ratio represent violinists and each part is 4 people. Therefore, we multiply the number of parts by the number of people that each part represents.
Violinists
4 parts in the ratio represent violinists and each part is 4 people. Therefore, we multiply the number of parts by the number of people that each part represents.
There are 16 violinists
Double bassists
1 part in the ratio represents double bassists, and each part represents 4 people.
Double bassists
1 part in the ratio represents double bassists, and each part represents 4 people.
There are 4 double bassists.
Total Number of Musicians
We are then asked to work out how many musicians there are in the band. Like the question before, there are two ways that we can work out how many members of the orchestra there are.
The first method is to add the number of cellists (which we are given in the question) to the number of violinists and double bassists that we found in the first part of this question. When we do this, we see that there are 28 members in the orchestra (8 + 16 + 4 = 28)
The second method is to work out how many parts there are in the ratio and multiply the number of parts by the amount that 1 part represents. There are 7 parts in the ratio (4 + 2 + 1) and each of these parts represents 4 members. We therefore multiply 7 by 4, which tells us that there are 28 members in the orchestra and this is the same answer that we obtained when we were using the previous method.
Total Number of Musicians
We are then asked to work out how many musicians there are in the band. Like the question before, there are two ways that we can work out how many members of the orchestra there are.
The first method is to add the number of cellists (which we are given in the question) to the number of violinists and double bassists that we found in the first part of this question. When we do this, we see that there are 28 members in the orchestra (8 + 16 + 4 = 28)
The second method is to work out how many parts there are in the ratio and multiply the number of parts by the amount that 1 part represents. There are 7 parts in the ratio (4 + 2 + 1) and each of these parts represents 4 members. We therefore multiply 7 by 4, which tells us that there are 28 members in the orchestra and this is the same answer that we obtained when we were using the previous method.