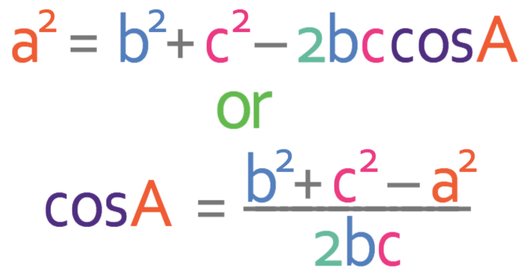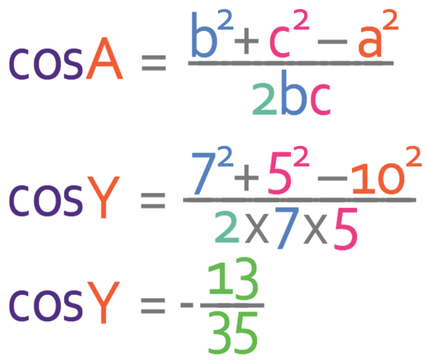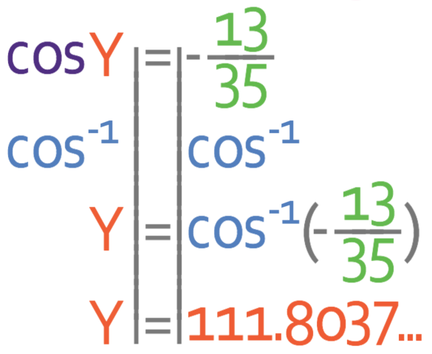Back to Edexcel Trigonometry (H) Home
4.10 O) The Cosine Rule – Finding an Angle
4.10 O) The Cosine Rule – Finding an Angle
The previous section introduced the cosine rule and we had an example of finding the length of an unknown side. In this section, we are going to be looking at an example whereby we are finding an angle.
The two versions of the cosine rule are given below.
The two versions of the cosine rule are given below.
Example 1 – Finding an Angle
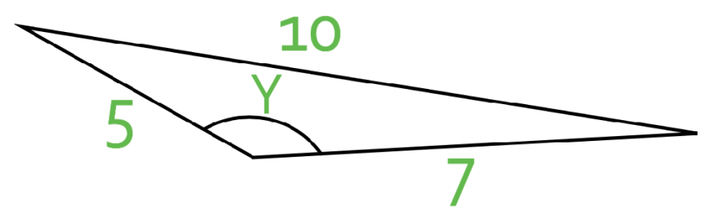
What is the size of the angle y in the triangle below? Give your answer to 1 decimal place.
What is the size of the angle y in the triangle below? Give your answer to 1 decimal place.
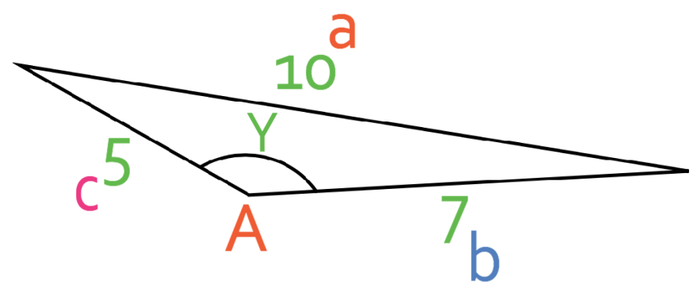
The first step in answering this question is to label up the sides and angles that we are given or asked to find. The best way to start labelling the triangle is to label the angle first. This is because there is only one angle in the cosine rule. The angle in the cosine rule is labelled A. This means that the side that is opposite angle A will be labelled a (this is the side that has a length of 10). It does not matter which of the other two sides are labelled b and c; I am going to label the side that has a length of 7 b and the side that has a length of 5 c.
We are now ready to use the cosine rule. As we are looking for an angle, it is easier to use the second version of the cosine rule that that has cosA as the subject.
We have found the value for cosY, but we are looking for Y. This means that we need to get rid of the cos, which we do by taking the inverse of cos for both sides; the inverse of cos is cos-1.
We are asked to give the answer to 1 decimal place.
Therefore, the answer is 111.8°.
Final Note
The best way to know whether you should use the sin rule or cosine rule is to label the triangle with all of the information that you are given/ want to find. After you have labelled the triangle, you can then see whether you need to use the sine or the cosine rule:
The best way to know whether you should use the sin rule or cosine rule is to label the triangle with all of the information that you are given/ want to find. After you have labelled the triangle, you can then see whether you need to use the sine or the cosine rule:
- To be able to use the sin rule, you need to have/ want to find 2 angle and 2 opposite side lengths
- To be able to use the cosine rule, you need to have/ want to find 1 angle and all 3 sides