Back to Edexcel Transformations (H) Home
4.3 A) Reflection: Undertaking – Part 1
4.3 A) Reflection: Undertaking – Part 1
Transformations change the size or position of a shape. We are going to be looking at a variety of different transformations during this section, such a reflections, rotations and enlargement.
We are going to start by looking at reflection.
We are going to start by looking at reflection.
Reflection
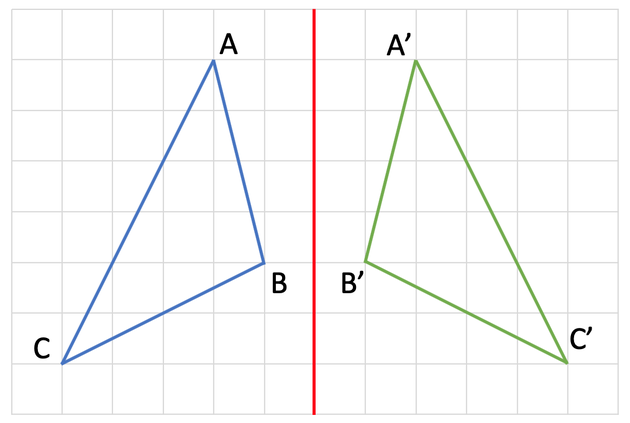
A shape can be reflected across a line of reflection (which is also known as a mirror line) to create an image. The triangle ABC has been reflected through the mirror line below to create the image, which is triangle A’B’C’. The mirror line on the diagram below is the red line.
A shape can be reflected across a line of reflection (which is also known as a mirror line) to create an image. The triangle ABC has been reflected through the mirror line below to create the image, which is triangle A’B’C’. The mirror line on the diagram below is the red line.
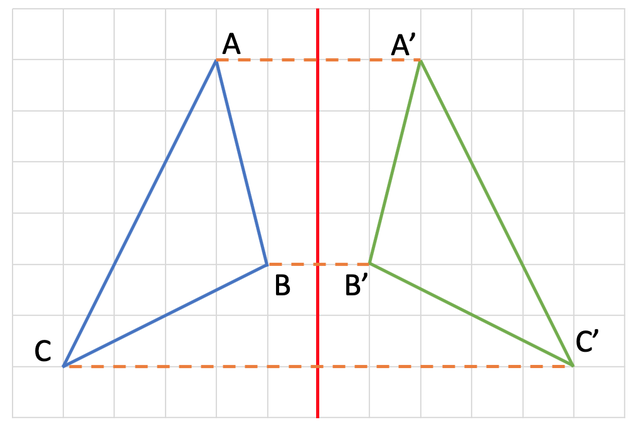
We are able to undertake a reflection by drawing lines that are perpendicular between the point on the shape and the line of reflection. Perpendicular means that the lines that we are drawing meet the reflection line at 90°. We then continue the line through the reflection line. I have drawn lines for these points on the diagram below.
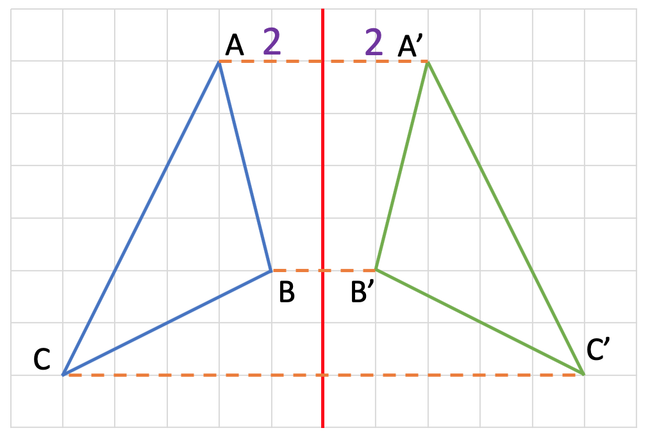
The distance between the point on the shape and the mirror line will be the same as the distance between the mirror line and the respective point on the image. Let’s see that this is the case by looking at point A on the shape and A’ on the image. The distance between point A and the mirror line is 2 squares. This is the same distance as the distance between A’ and the mirror line.
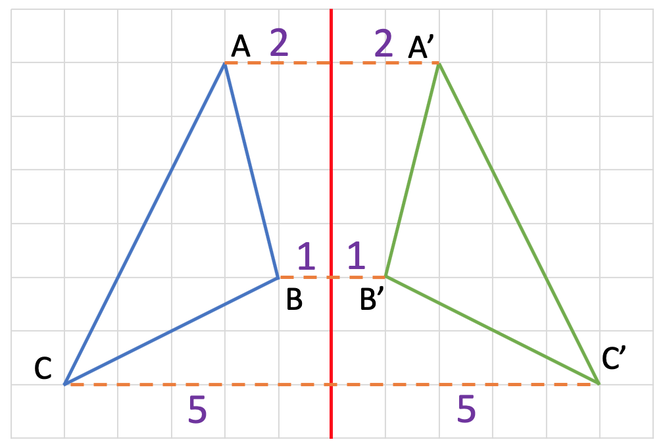
We can do the same for the other two points on the shape and the image. The distance between point B and the mirror line is 1 square, which is the same as the distance between B’ and the mirror line. Also, the distance between point C and the mirror line is 5 squares, which is the same as the distance between C’ and the mirror line.
Example 1
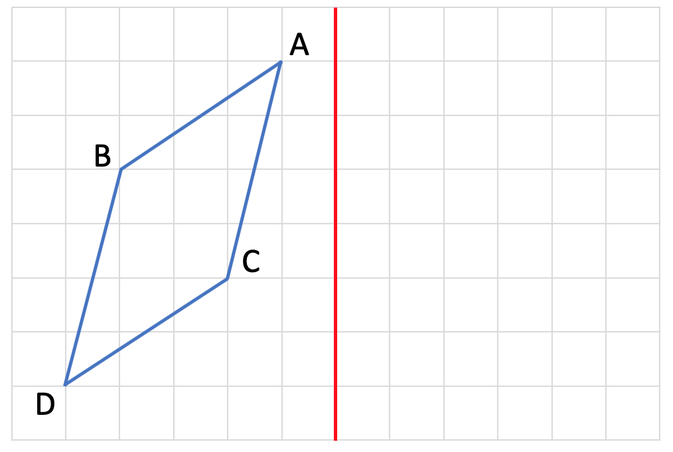
Reflect the shape below in the mirror line. The mirror line is the red line. Click here for a printable version of the examples in this section.
Reflect the shape below in the mirror line. The mirror line is the red line. Click here for a printable version of the examples in this section.
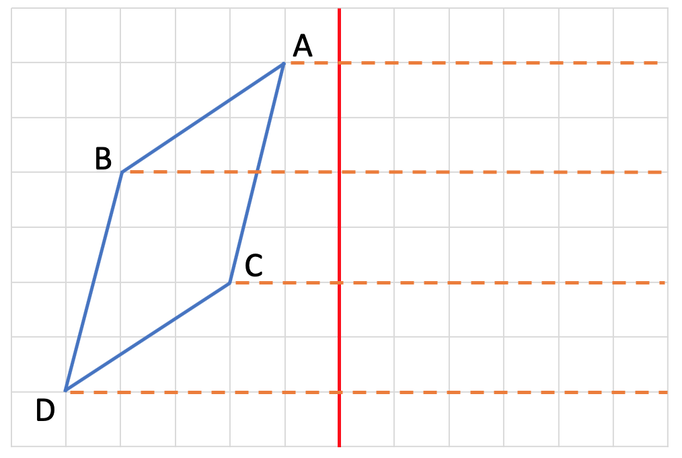
The first step in answering this question is to draw 4 lines going from the 4 points on the above shape to and through the mirror line. These lines need to be perpendicular to the mirror line (they need to meet the mirror line at 90°).
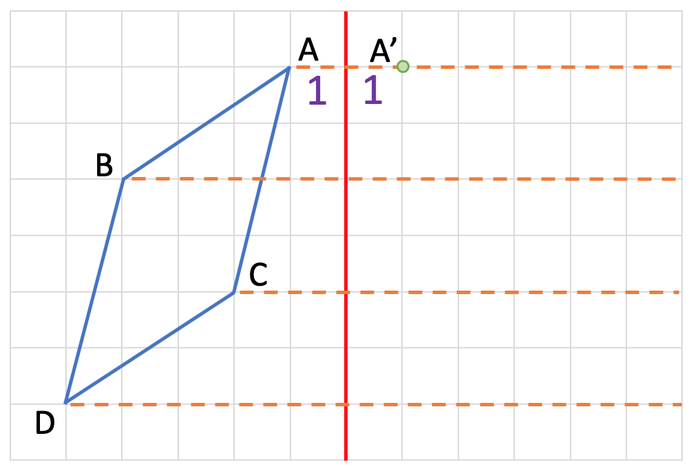
Let’s start by looking at the point A. The distance between point A and the mirror line will be the same as the distance between the respective point (A’) on the image. The distance between A and the mirror line is 1 square. Therefore, the distance between the mirror line and A’ will also be 1 square. A’ is shown on the diagram below:
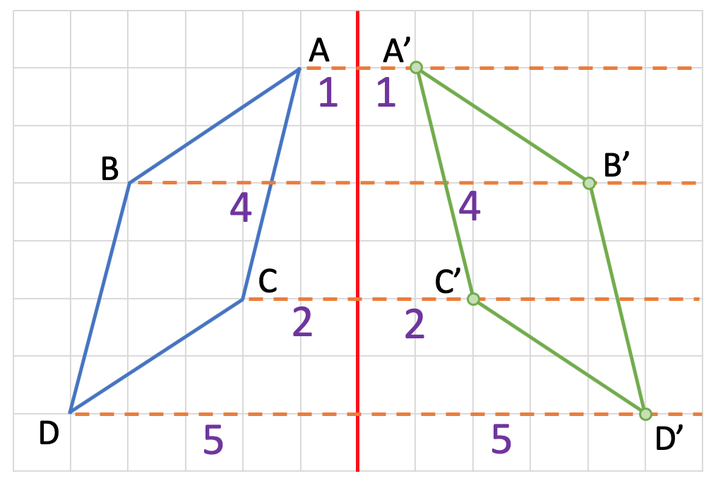
We now do the same for the other 3 points:
The final step is to connect all of the points together to create the image. The image is shown below.
- B is 4 squares away from the mirror line, so B’ will also be 4 squares from the mirror line
- C is 2 squares away from the mirror line, so C’ will also be 2 squares from the mirror line
- D is 5 squares away from the mirror line, so D’ will also be 5 squares from the mirror line
The final step is to connect all of the points together to create the image. The image is shown below.
Example 2
Sometimes it will be the case that we are given a shape on a graph and we are asked to reflect the shape through a line that has an equation. We are going to be using a horizontal and vertical line in this example (we are going to be looking at upwards or downwards sloping line in the next section).
In the linear graph section, we learnt that vertical lines take the form of x = “something” and horizontal lines take the form of y = “something”. Click here if you would like to know more about vertical and horizontal lines.
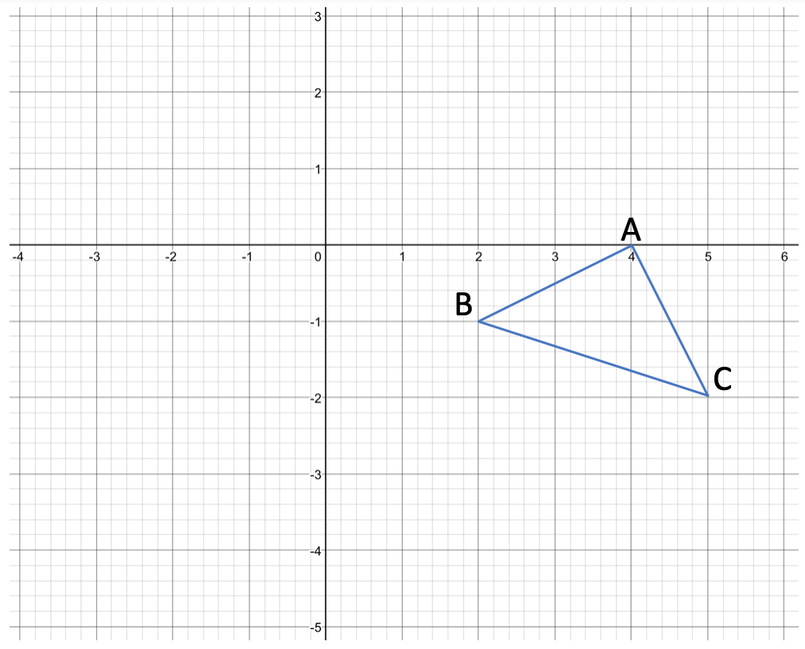
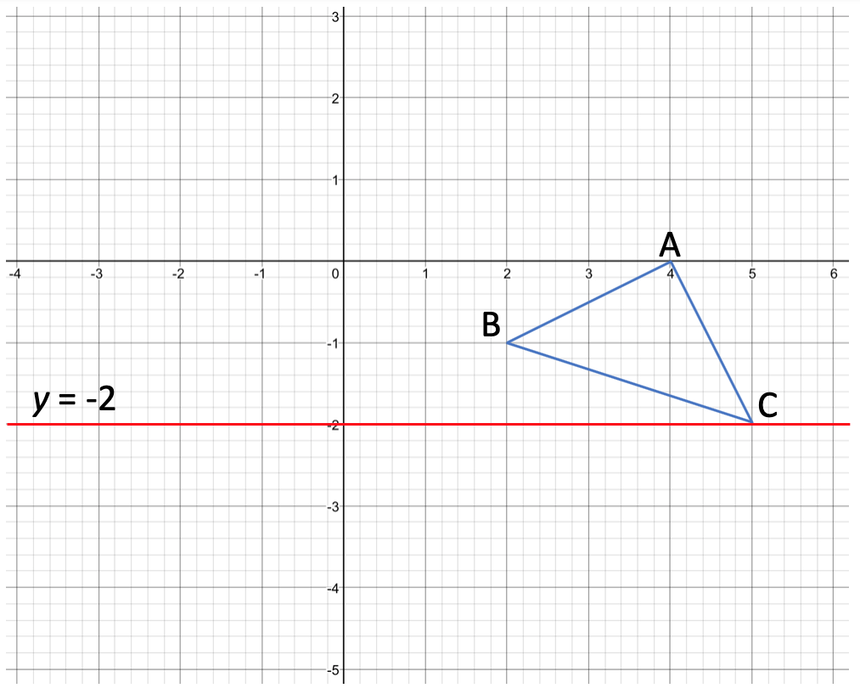
A triangle is drawn on the graph below.
Sometimes it will be the case that we are given a shape on a graph and we are asked to reflect the shape through a line that has an equation. We are going to be using a horizontal and vertical line in this example (we are going to be looking at upwards or downwards sloping line in the next section).
In the linear graph section, we learnt that vertical lines take the form of x = “something” and horizontal lines take the form of y = “something”. Click here if you would like to know more about vertical and horizontal lines.
A triangle is drawn on the graph below.
Complete the following:
Part 1
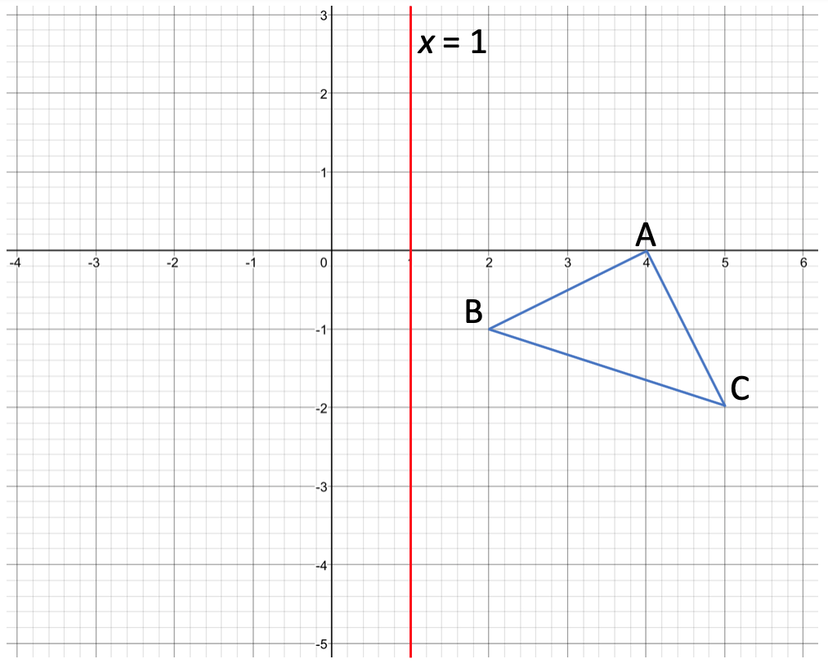
Part 1 asks us to reflect the triangle in the line x = 1. This line is a vertical line and we draw this line by finding where x is equal to 1 on the x axis. We then draw a vertical line passing through this point. The line is drawn on the graph below.
- Reflect the triangle through the line x = 1
- Reflect the triangle through the line y = -2
Part 1
Part 1 asks us to reflect the triangle in the line x = 1. This line is a vertical line and we draw this line by finding where x is equal to 1 on the x axis. We then draw a vertical line passing through this point. The line is drawn on the graph below.
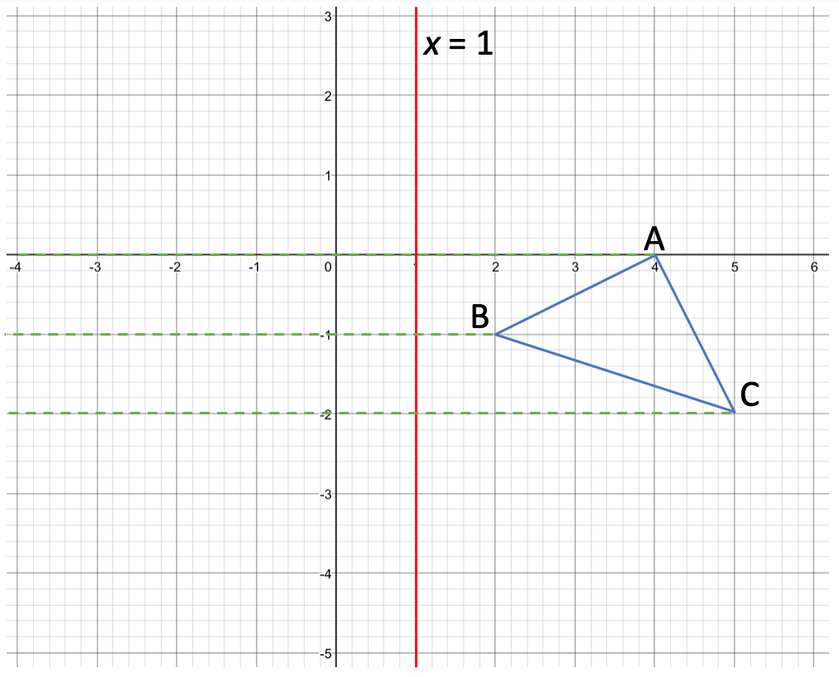
We now have the shape that we are reflecting and the mirror line. The next step is to draw lines going from the points on the shape to and through the mirror line. These lines must be perpendicular to the mirror line.
The next step is to plot the points on the image. We know that when reflecting a shape, the distance between a particular point on the shape and the mirror line will be the same as the distance between the respective point on the image and the mirror line.
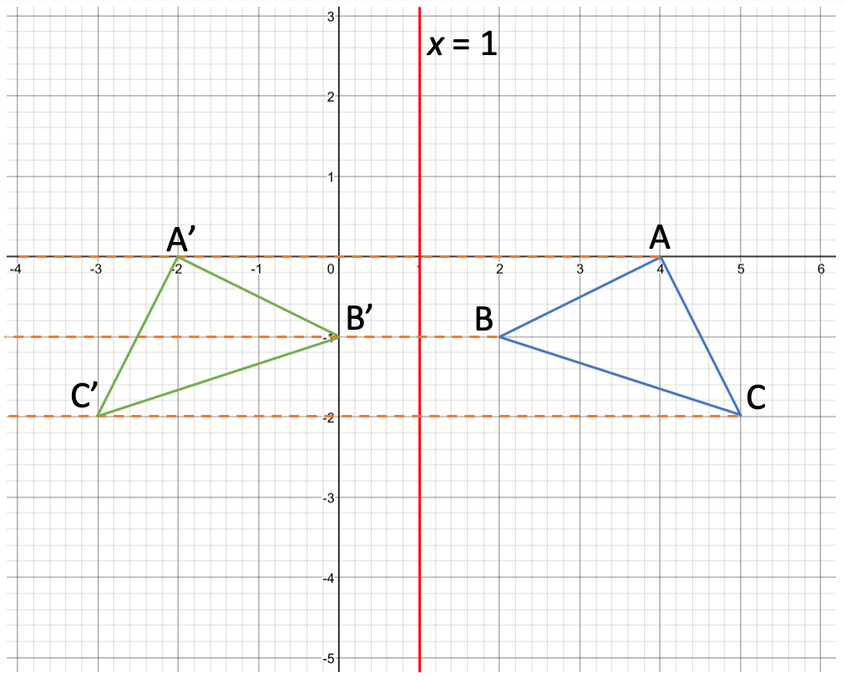
The final step is to connect all of the points to create the image. The image is shown on the diagram below.
The final step is to connect all of the points to create the image. The image is shown on the diagram below.
Part 2
Part 2 asks us to reflect the triangle in the line y = -2. This is a horizontal line and we draw the horizontal line by finding where y is equal to -2 on the y axis. We then draw a horizontal line passing through this point. The line y = -2 is shown below.
Part 2 asks us to reflect the triangle in the line y = -2. This is a horizontal line and we draw the horizontal line by finding where y is equal to -2 on the y axis. We then draw a horizontal line passing through this point. The line y = -2 is shown below.
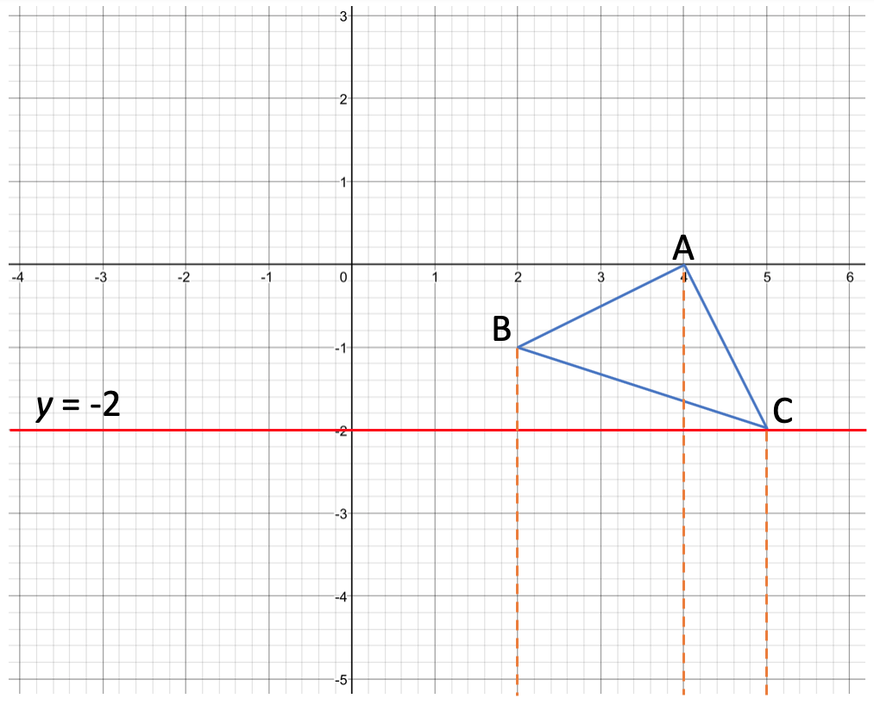
We now have a shape and a mirror line. The next step is to draw lines going from the points on the triangle to and through the mirror line; these lines need to be perpendicular to the mirror line.
We now make sure that the distances between the points on the shape and the mirror line are the same as the distances between the mirror line and the respective points on the image.
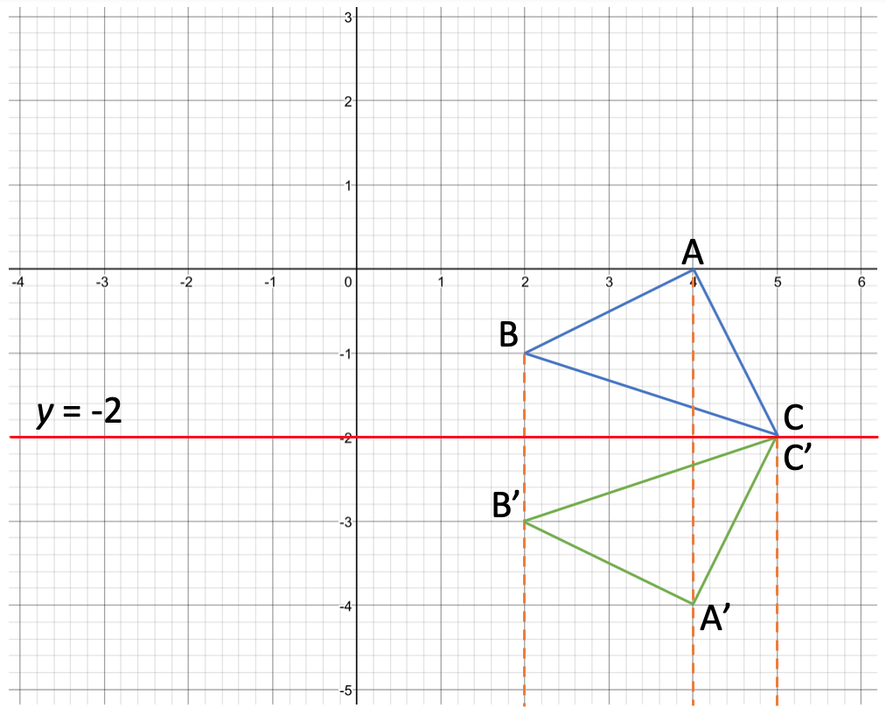
The final step is to connect all of the points to create the image. The image is shown on the diagram below.
The final step is to connect all of the points to create the image. The image is shown on the diagram below.