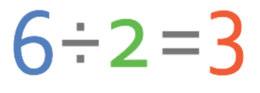Back to Edexcel Transformations (H) Home
4.3 H) Enlargements: Normal – Part 2
4.3 H) Enlargements: Normal – Part 2
We are now going to have a look at finding out what the enlargement is for a shape. Whenever we are giving the enlargement of a shape, we need to give the scale factor and the centre of enlargement.
Example 1
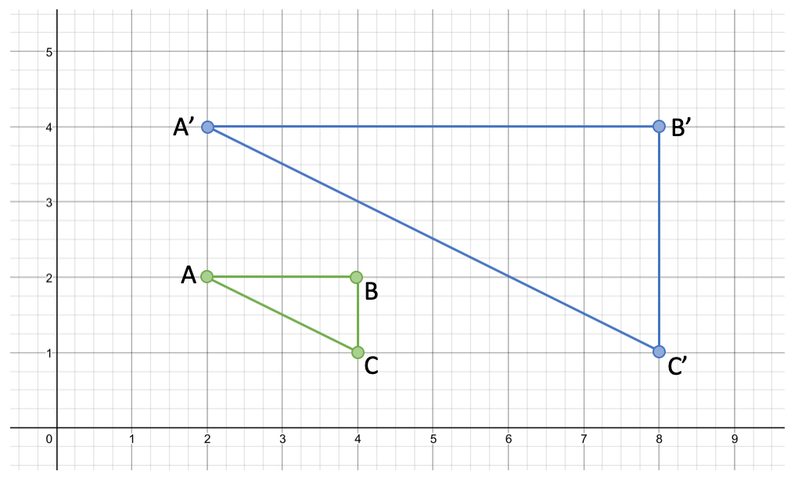
The shape ABC has been enlarged to make shape A’B’C’. Describe the enlargement. Click here for a printable version of this question.
The shape ABC has been enlarged to make shape A’B’C’. Describe the enlargement. Click here for a printable version of this question.
The easiest way to work out the scale factor is to look at the length of the respective sides for both the original shape and the enlarged shape. The respective lengths that I am going to use are A’B’ and AB. The length of A’B’ is 6 units and the length of AB is 2 units. We are able to work out the scale factor by dividing the length of one of the sides of the enlarged shape by the length of the respective side of the original shape. Therefore, we complete the calculation below:
This tells us that the scale factor is 3. It is worth using another side to double check that you have obtained the correct scale factor. I am going to use the sides B’C’ and BC. B’C’ is 3 units and BC is 1 unit. We work out the scale factor by dividing the length of a side in the enlarged shape by the length of the respective side in the original shape. Therefore, we divide 3 by 1, which gives us 3. This is exactly the same scale factor as we obtained from the previous sides, thus indicating that we have found the correct scale factor. You do not have to do this, but it worth doing this to check that you have obtained the correct scale factor.
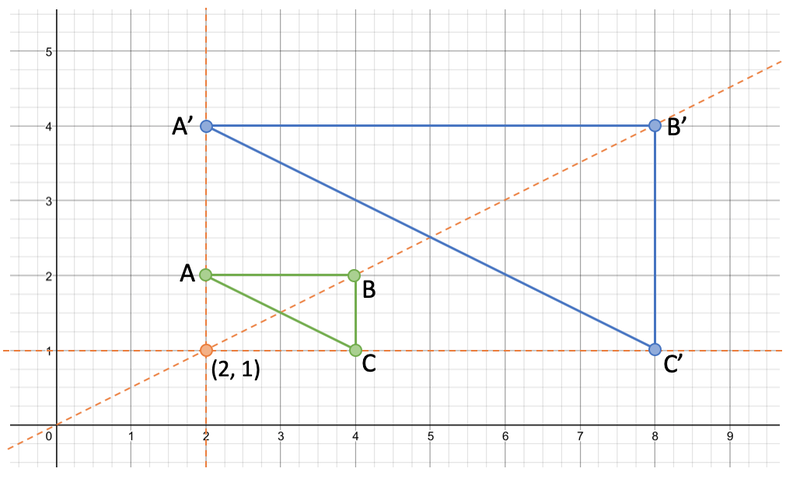
We now need to find the centre of enlargement. We are able to do this by drawing lines connecting the respective points/ corners of the original shape and the enlarged shape; we continue the lines past the points.
We now need to find the centre of enlargement. We are able to do this by drawing lines connecting the respective points/ corners of the original shape and the enlarged shape; we continue the lines past the points.
The point where all of the lines that you have drawn intercept one another is the centre of enlargement. On the above diagram, you can see that the centre of enlargement has the coordinates (2, 1).
Therefore, the shape A’B’C’ is an enlargement of shape ABC by a scale factor of 3 from the point (2, 1).
Therefore, the shape A’B’C’ is an enlargement of shape ABC by a scale factor of 3 from the point (2, 1).