Back to Edexcel Transformations (H) Home
4.3 L) Invariant Points
4.3 L) Invariant Points
Sometimes some of the points on a shape after a transformation has taken place are invariant. Invariant means that the point remains in the same position; the coordinates of the point before the transformation and after the transformation are the same. You may be asked at the end of a transformation question to give the coordinates of the point or points that are invariant. We are going to have a look at an example in this section.
Example 1
Click here for a printable PDF of the graph for this question.
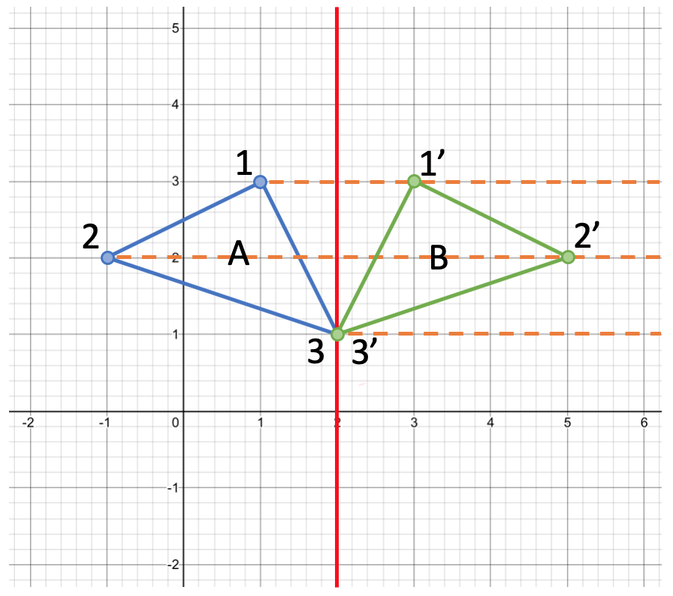
Triangle A is reflected in the line x = 2 to create triangle B.
Click here for a printable PDF of the graph for this question.
Triangle A is reflected in the line x = 2 to create triangle B.
One of points on triangle A is invariant under the transformation. Find the coordinates for this invariant point.
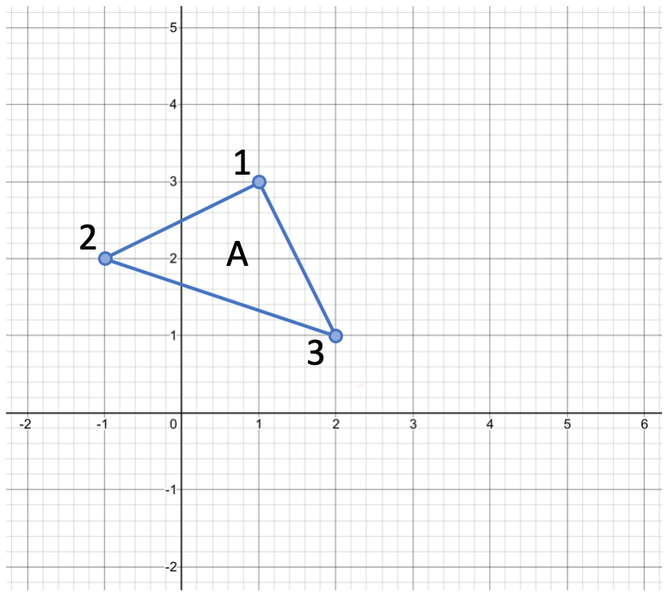
Before we start answering this question, I am going to label the points on the triangle 1, 2 and 3. The labelled points are shown below.
Before we start answering this question, I am going to label the points on the triangle 1, 2 and 3. The labelled points are shown below.
We now answer the question by carrying out the reflection in the usual way. After we have completed the reflection, we then compare the points on triangle A and triangle B (the reflected triangle) to find the point that is invariant (in the same position).
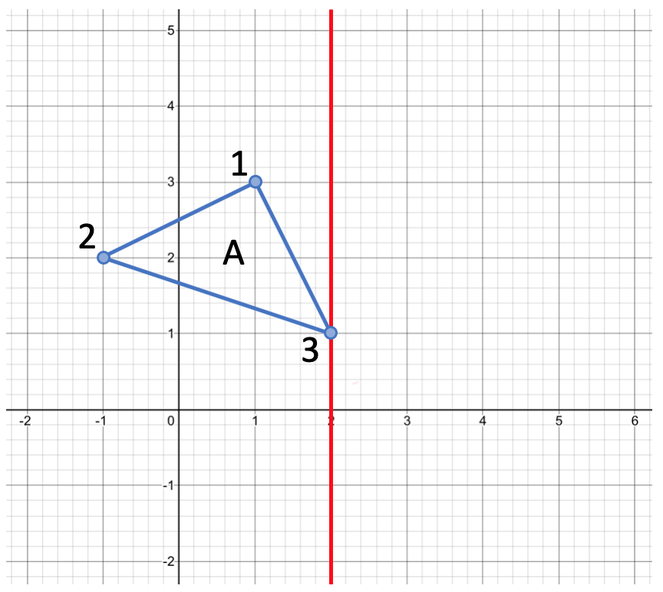
The first step when reflecting a shape is to draw the mirror line. The mirror line for this question is x = 2. This line takes the form x = “something”, which means that it is a vertical line. We draw the line x = 2 by finding where x is 2 and drawing vertically up and down. The line x = 2 is shown in red on the graph below.
The first step when reflecting a shape is to draw the mirror line. The mirror line for this question is x = 2. This line takes the form x = “something”, which means that it is a vertical line. We draw the line x = 2 by finding where x is 2 and drawing vertically up and down. The line x = 2 is shown in red on the graph below.
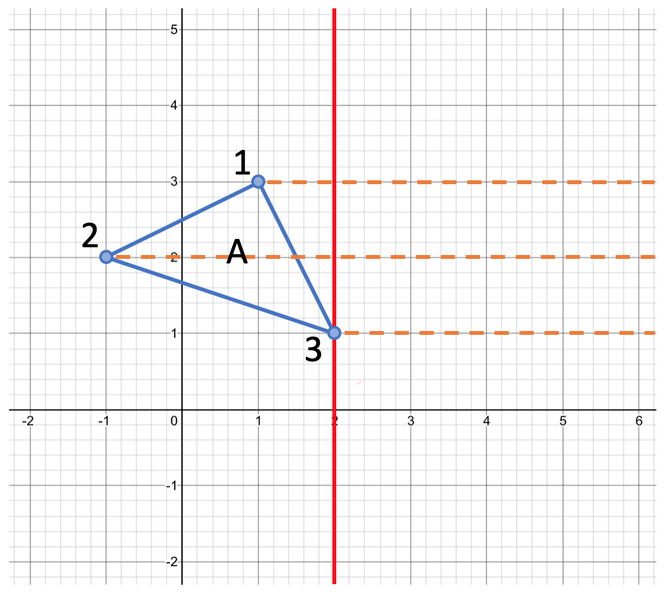
The next step is to draw faint lines from the corners of the triangle to and through the mirror line. These lines must be perpendicular to the mirror line (perpendicular means that the faint lines that we are drawing must pass through the mirror line at 90°).
The next step is to plot the corners on the image (the reflected triangle). We know that when we reflect a shape, the distance between a particular point on the shape and the mirror line will be the same as the distance between the respective point on the image and the mirror line. For example, the distance between point 1 and the mirror line is 1 square, and this means that the distance between point 1’ on the image and the mirror line will also be 1 square.
We do the same for the other two points on the triangle and join the points up to create triangle B. Triangle B is shown on the graph below.
We do the same for the other two points on the triangle and join the points up to create triangle B. Triangle B is shown on the graph below.
We now compare the points on triangle A and triangle B to find the point that is invariant (in the same position). When we compare points, we see that 3 and 3’ are the same, and this means that this point is invariant. The coordinates of this point are (2, 1). Therefore, the answer to this question is that the coordinates for the point that is invariant are (2, 1).
End Note
The key thing to remember from this section is that invariant means the same. It is worth getting this definition down on a revision card because it is an easy definition to forget.
Usually we only see invariant questions at the end of transformation questions. When this is the case, we complete the transformation in the usual way. We then we compare the points on the shape before and after the transformation has taken place to find the coordinates of the point/points that is/are invariant.
The key thing to remember from this section is that invariant means the same. It is worth getting this definition down on a revision card because it is an easy definition to forget.
Usually we only see invariant questions at the end of transformation questions. When this is the case, we complete the transformation in the usual way. We then we compare the points on the shape before and after the transformation has taken place to find the coordinates of the point/points that is/are invariant.