Back to Edexcel Similar Shapes (H) Home
4.4 B) Congruent Triangles – Part 1
4.4 B) Congruent Triangles – Part 1
Congruent triangles are triangles that are identical in shape and size. There are 4 different ways that we can prove that triangles are congruent. It is worth making a note of these rules on revision cards.
Way 1 – SSS
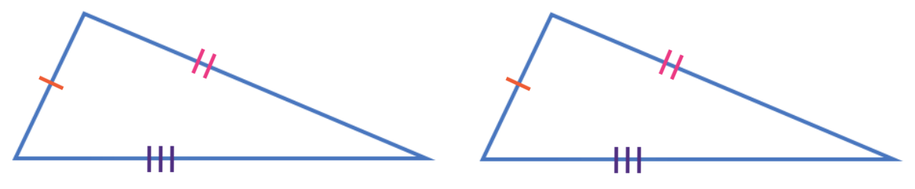
We can prove that two triangles are congruent if the triangles have three sides that are the same. This is known as the Side-Side-Side rule, which we refer to as SSS. The notation for equal sides is a dash through the sides that are equal. If we have a second pair of equal sides, we use two dashes, and we use 3 dashes for a third pair of equal sides etc…
We can prove that two triangles are congruent if the triangles have three sides that are the same. This is known as the Side-Side-Side rule, which we refer to as SSS. The notation for equal sides is a dash through the sides that are equal. If we have a second pair of equal sides, we use two dashes, and we use 3 dashes for a third pair of equal sides etc…
From the above diagram, we can see that we have 3 pairs of sides that are equal in length. Therefore, these two triangles are congruent.
Way 2 – AAS
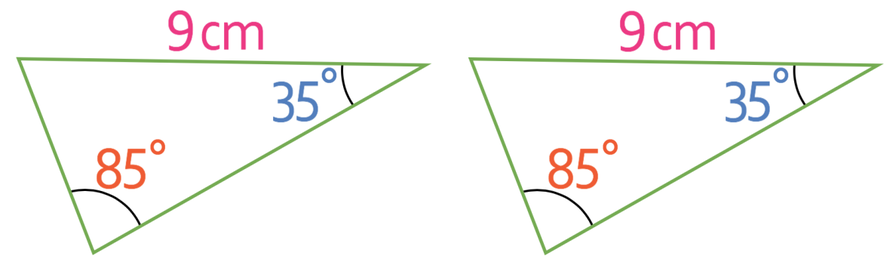
Another way that we can prove that triangles are congruent is if we have two angles that are the same and a corresponding side that is the same length (the corresponding side must be in the same location in both of the triangles). This rule is known as the Angle-Angle-Side rule (AAS) or the Angle-Side-Angle rule (ASA).
Another way that we can prove that triangles are congruent is if we have two angles that are the same and a corresponding side that is the same length (the corresponding side must be in the same location in both of the triangles). This rule is known as the Angle-Angle-Side rule (AAS) or the Angle-Side-Angle rule (ASA).
From the above diagram we can see that both of the triangles have an angle of 35° and 85°. Also, the side that creates the 35° angle and the angle that is unknown on both the triangles is the same length (they are both 9 cm). Therefore, we have two angles and a corresponding side that are the same, which means that these triangles are congruent.
Way 3 – SAS
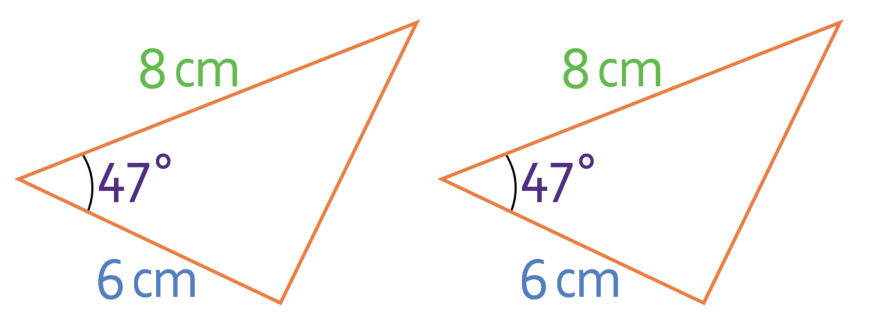
We can prove that two triangles are congruent if two lengths and the angle between the two lengths are equal to one another in the triangles. This rule is known as the Side-Angle-Side rule, which we can refer to as SAS.
We can prove that two triangles are congruent if two lengths and the angle between the two lengths are equal to one another in the triangles. This rule is known as the Side-Angle-Side rule, which we can refer to as SAS.
From the above diagram, we can see that both of the triangles have a side that is 6 cm and 8 cm. Also, the angle on both of the triangles that is between the sides that are 6 cm and 8 cm is 47°. Therefore, we can say that these two triangles are congruent to one another due to the SAS rule.
Way 4 – RHS
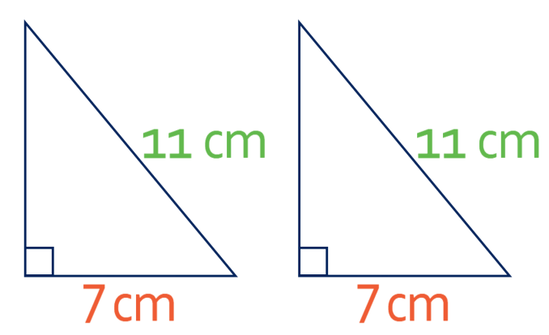
The final way of proving congruent triangles involves right-angle triangles and we can only use this rule for right-angle triangle. The rules states that right-angle triangles will be congruent if the triangles have a right-angle, a hypotenuse that is the same length and a corresponding side that is the same length. The hypotenuse of a right-angle triangle is the longest side in the right-angle triangle; it is the side that is on the other side to the right-angle.
The final way of proving congruent triangles involves right-angle triangles and we can only use this rule for right-angle triangle. The rules states that right-angle triangles will be congruent if the triangles have a right-angle, a hypotenuse that is the same length and a corresponding side that is the same length. The hypotenuse of a right-angle triangle is the longest side in the right-angle triangle; it is the side that is on the other side to the right-angle.
Both of the triangles are right-angled triangles. We can tell this because they both have a small square in one of their angles. The hypotenuses of both of the triangles are 11 cm. Also, for both triangles we have a corresponding length that is the same; this side is 7 cm for both triangles. Therefore, these two triangles are congruent because of the RHS rule (Right-angle-Hypotenuse-Side).
DO NOT
Congruent shapes are shapes that are the same in shape and size; both of these must be met in order for shapes to be congruent to one another.
The reason why I say this is because sometimes students make the mistake and say that triangles are congruent if all of the angles in the triangles are the same and this is not true. If all of the angles are the same in a triangle, it means that the shape of the triangles are the same; the triangles are similar to one another (we will look at similar shapes later in this section). However, it does not prove that the shapes are the same size. In order to prove that the shapes are the same size, we need one corresponding size.
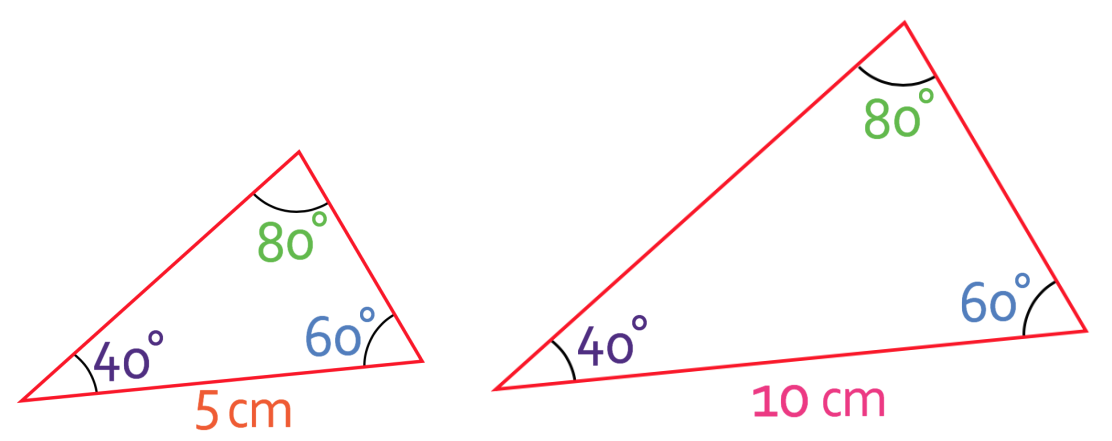
For example, there are two triangles below.
Congruent shapes are shapes that are the same in shape and size; both of these must be met in order for shapes to be congruent to one another.
The reason why I say this is because sometimes students make the mistake and say that triangles are congruent if all of the angles in the triangles are the same and this is not true. If all of the angles are the same in a triangle, it means that the shape of the triangles are the same; the triangles are similar to one another (we will look at similar shapes later in this section). However, it does not prove that the shapes are the same size. In order to prove that the shapes are the same size, we need one corresponding size.
For example, there are two triangles below.
The angles in the two triangles are the same, but we can see that the sides that connects the 40° and the 60° angles are not equal to one another; it is 5 cm in the smaller triangle and 10 cm in the larger triangle. This means that the shapes are not the same size, and therefore, they are not congruent to one another.
The key rule to take from this example is that you can never prove that triangles are congruent by having 3 angles.
The key rule to take from this example is that you can never prove that triangles are congruent by having 3 angles.