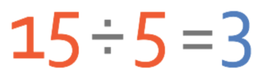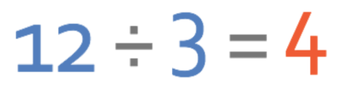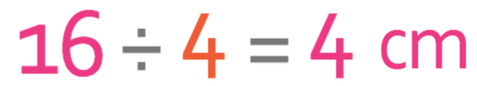Back to Edexcel Similar Shapes (H) Home
4.4 D) Similar Shapes: Length
4.4 D) Similar Shapes: Length
Scale factors appear in a few different sections in maths. We can use scale factors to compare different sized shapes that are mathematically similar. Mathematically similar shapes are where the respective angles in the two similar shapes are the same and the respective sides of the two similar shapes are in the same proportion.
A scale factor that is greater than 1 will increase the length (surface area and volume) of a shape and a scale factor that is less than 1 will decrease the length (surface area and volume) of a shape.
A scale factor that is greater than 1 will increase the length (surface area and volume) of a shape and a scale factor that is less than 1 will decrease the length (surface area and volume) of a shape.
Example 1
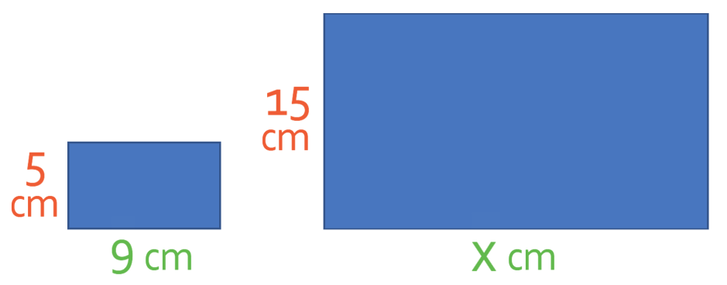
Let’s have an example. We have two rectangles that are mathematically similar. The smaller rectangle’s shortest side has a length of 5 cm and it’s longest side is 9 cm. The shortest side of the larger shape is 15 cm and it’s longest side is unknown. What is the scale factor and what is the length of the larger shape’s longest side?
Let’s have an example. We have two rectangles that are mathematically similar. The smaller rectangle’s shortest side has a length of 5 cm and it’s longest side is 9 cm. The shortest side of the larger shape is 15 cm and it’s longest side is unknown. What is the scale factor and what is the length of the larger shape’s longest side?
The first step to answering this question is to find out what the scale factor of enlargement is. In order to work the scale factor out, we need to use the values of corresponding side. In the question, we are given the values for the shortest sides of both of the rectangles. The shortest side of the smaller rectangle has a length of 5 cm and the shorter side in the larger rectangle has a length of 15 cm. We are able to work out the scale factor by dividing the larger length by the shorter length.
This tells us that the scale factor is 3. We are now able to find the length of the longer side in the larger rectangle and we do this by multiplying the longer side in the smaller shape by the scale factor that we have just found. The longer side in the small rectangle has a length of 9 cm.
Therefore, the larger rectangle’s longest side is 27cm.
Key Points
We always find the scale factor by dividing the larger corresponding side by the shorter corresponding side. What we do when we have found the scale factor depends on what we are looking for:
We always find the scale factor by dividing the larger corresponding side by the shorter corresponding side. What we do when we have found the scale factor depends on what we are looking for:
- If we are finding a length on the larger shape, we multiply by the scale factor. This was the case with example 1; we wanted to find the length on the larger shape, so we multiplied the corresponding side in the smaller shape by the scale factor (we multiplied by 3)
- If we are finding a length on the smaller shape, we divide by the scale factor. Example 2 is will involving dividing by the scale factor rather than multiplying by the scale factor.
Example 2
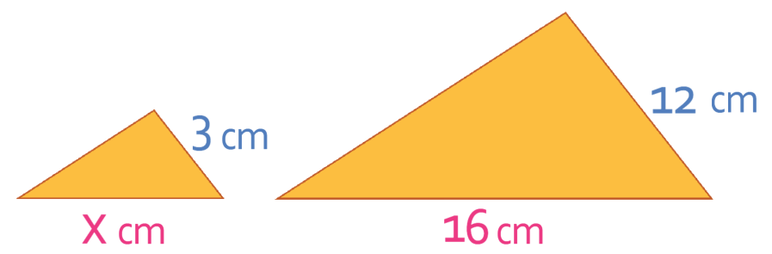
The two shapes below are mathematically similar. What is the length of the side labelled x?
The two shapes below are mathematically similar. What is the length of the side labelled x?
The first step in answering this question is to find out what the scale factor is. We find the scale factor by dividing the larger corresponding side by the shorter corresponding side. We are given the side on the right in both the larger and the smaller shape; the side on the right in the smaller shape is 3 cm and the side on the right in the larger shape is 12 cm. Therefore, we find the scale factor by dividing 12 by 3.
The scale factor for these two similar shapes is 4. We are finding the length of a side on the smaller shape. This means that we need to divide the corresponding side on the larger shape by the scale factor. The corresponding side on the larger shape is 16 cm and the scale factor is 4. The calculation that we undertake is shown below.
The length of the side labelled x is 4 cm.
It is always a good idea to check that our answer makes sense and we do this by checking that the lengths of all of the sides on the smaller shape are smaller than their respective sides on the larger shape. This is because it is quite easy to multiply by the scale factor instead of dividing by the scale factor or vice versa.
It is always a good idea to check that our answer makes sense and we do this by checking that the lengths of all of the sides on the smaller shape are smaller than their respective sides on the larger shape. This is because it is quite easy to multiply by the scale factor instead of dividing by the scale factor or vice versa.