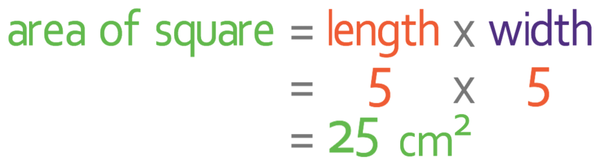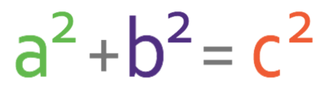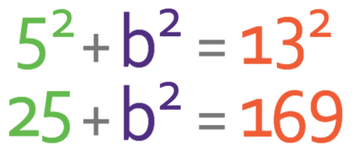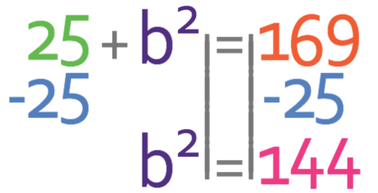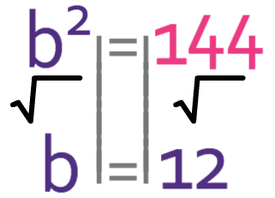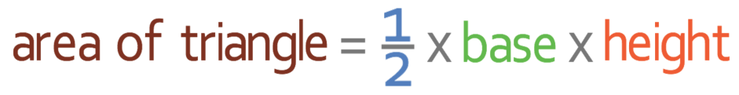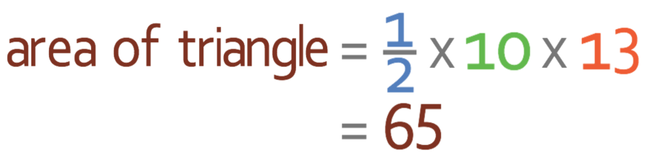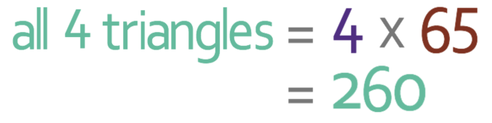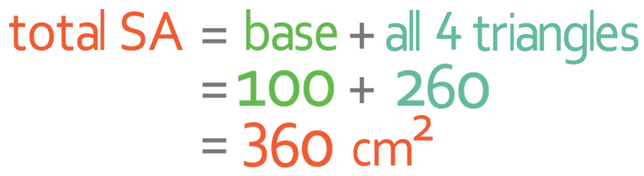Back to Edexcel 3D Shapes (H) Home
4.6 F) Pyramids
There are a few different types of pyramids that you will come across. The name of the pyramid comes from the polygon that is at the base of the pyramid. For example, a triangular-based pyramid has a triangle base; a square-based pyramid has a square base. The sides that are not the base of a pyramid are triangular and they all meet at the top. 
Volume of a Pyramid 
We are able to work out the volume of a pyramid by using the following formula:
Example 1 
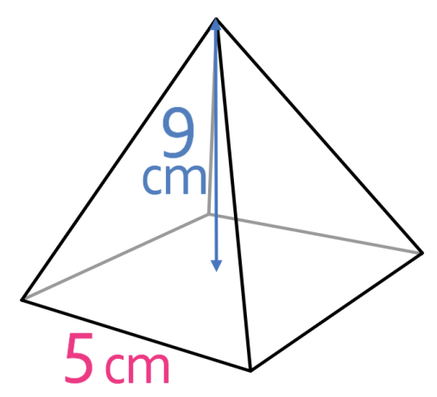
What is the volume of the following square-based pyramid?
We are going to be using the formula below to work out the volume of the pyramid:
In order to use the formula above, we need to know the area of the base and the perpendicular height. We know that the perpendicular height of the pyramid is 9 cm, but we do not know what the area of the base is.
 
The base of the pyramid is a square and we work out the area of a square by either multiplying the length by the width or squaring one of the sides. I am going to work out the area by multiplying the length by the width. The length and width for the square are 5 cm. 

The area of the base is 25 cm2.

 

We now sub in the area of the base (25 cm2) and the perpendicular height (9 cm) into the formula.

The volume of the pyramid is 75 cm3.

Example 2 
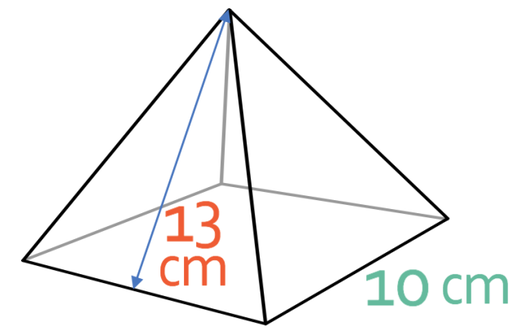
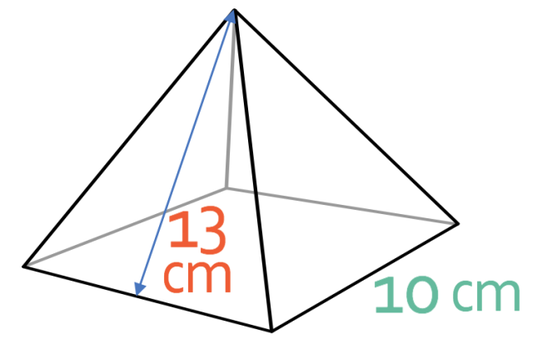
What is the volume of the square-base pyramid below?
We work out the volume of a pyramid by using the formula below:

We need to have the area of the base and the perpendicular height in order to use the above formula.

 

Let’s first work out the area of the base of the pyramid first. The base is a square and the lengths of each side of the square are 10 cm. We work out the area of a square by multiplying the length by the width (or squaring one of the sides). Therefore, the area of the base of the pyramid is 100 cm2 (10 x 10).

 

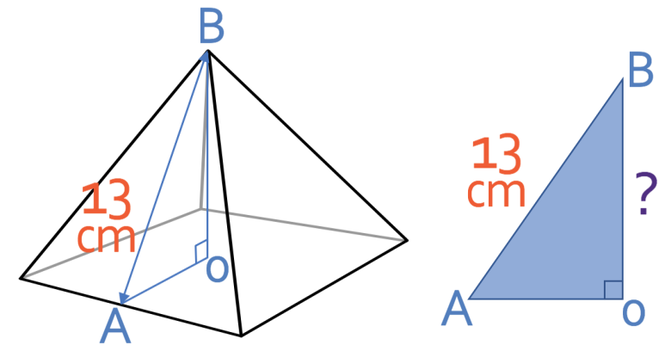
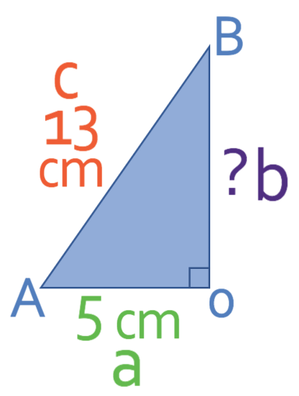
We also need to know the perpendicular height of the pyramid. The perpendicular height is measured at a right angle from the centre of the base of the pyramid to the top of the pyramid. The diagram does not give us the perpendicular height of the pyramid. However, we are given the slanted height, which is the distance between the edge of the base of the pyramid and the top of the pyramid; the slanted height for the pyramid is 13 cm. We are able to work out the perpendicular height of the pyramid by creating a right-angle triangle whereby the three sides are the perpendicular height, the slanted height and the distance between where the slanted height starts on the centre of the base. The right-angle triangle and the points on the pyramid that create the right-angle triangle are shown below.

We need to find the length of AO. Each of the sides on the square base of the pyramid are 10 cm. The length AO will be half of the length of one of the sides. This is because AO is going from one side of the square to the centre of the base. Therefore, AO is 5 cm.

​We now have two sides on the right-angle triangle, which means that we can find the third side by using Pythagoras’ theorem. His theorem states that the hypotenuse squared is the sum of the squares of the other two sides. The formula is shown below:
In the formula above, c is the hypotenuse, and a and b are the other two sides (it does not matter which side is a and which side is b). The side that is 13 is the hypotenuse, which means that this side has to be c. I am then going to let a be 5 and b be the perpendicular height (the side that is unknown). The labelled right-angle triangle is shown below.
We can now sub the values into the formula; we sub in a as 5 and c as 13.
​The first step in finding the value of b is to move the 25 from the left side to the right. We are able to do this by doing the opposite; we take 25 from both sides of the equation. 

We want to find the value of b and not b2. Therefore, we need to square root both sides of the equation.

The perpendicular height of the pyramid is 12 cm. We are now able to use the volume of a pyramid formula. 

The volume of the pyramid is 400 cm3.

Surface Area 
To find the surface area of a pyramid, we add the area of each of the individual faces together. The number of faces will depend on what the base of the pyramid is. For example, when we have a triangular-base pyramid, there will be 4 faces; 1 of these faces will be the base and the other 3 faces will be the faces that go from the base to the top point. A square-base pyramid will have 5 faces; 1 of the faces will be the base and the other 4 faces will be the faces that go from the base to the top of the pyramid.
 
Let’s work out the surface area of the square-based pyramid in the second example. 

There are 5 faces on this pyramid. We have already worked out the area of the base, which is 100 cm2 (10 x 10). We now need to work out the area of the other 4 faces and the area of all of these 4 faces are the same. These faces are triangles and the formula for working out the area of a triangle is:

​Each of the triangles has a base of 10 cm and a height of 13 cm. We sub these values into the formula to work out the area of one of the triangles. 

The area of one triangle is 65 cm2. There are four triangles, which means that we need to multiply 65 cm2 by 4 to work out the area of all four of the triangles.

The final step is to add this area to the area of the base.

The total surface area of this pyramid is 360 cm2.