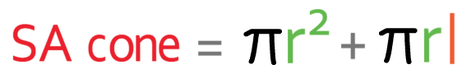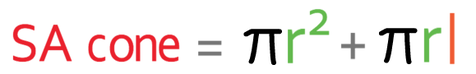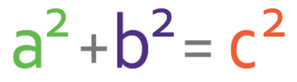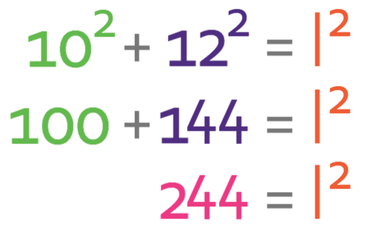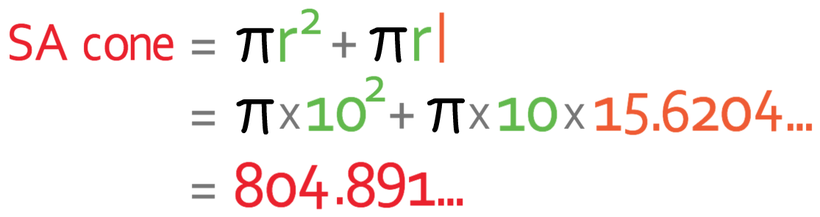Back to Edexcel 3D Shapes (H) Home
4.6 H) Cones – Part 2
​In the previous section, we learnt that the formula for working out the surface area of a cone is:
​r in the formula above is the radius an l is the slanted height.
Example 1 – Surface Area 
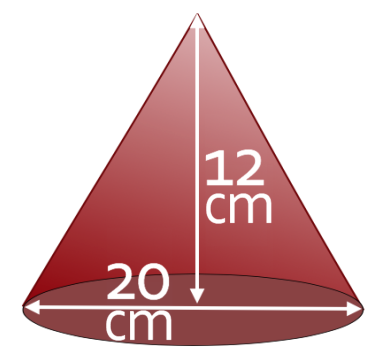
Find the surface area of the cone below and give your answer to one decimal place (the cone below is the same came as the cone in example 1 in the previous section). 
We can work out the surface area of a cone by using the formula below:
In order to use the above formula, we need to have the radius and the slanted height. We are told that the diameter of the cone is 20 cm. The radius is half the length of the diameter, and this means that the radius is 10 cm (20 ÷ 2).
 
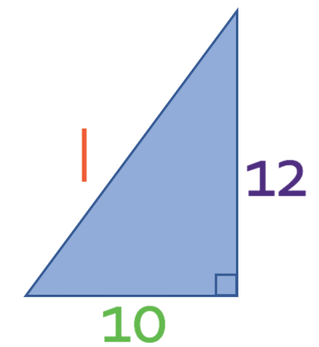
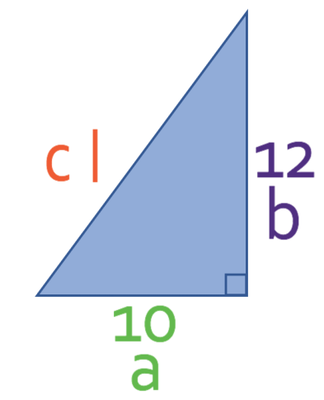
We now need to find the slanted height. We are able to find the slanted height by creating a right-angled triangle with the sides being the radius, the perpendicular height and the slanted height. The triangle is shown below.
We can work out the slanted height by using Pythagoras’ theorem, which states that the hypotenuse squared is equal to the sum of the squares of the other two sides. His formula is given below:
c in the formula above is the hypotenuse, and a and b are the other two sides. The slanted height is the hypotenuse, which means that this side will be c. The other two sides will be a and b; it does not matter which side is which. I am going to let a be 10 and b be 12. The labelled triangle is shown below:
We can now sub a in as 10, b in as 12 and c as l into Pythagoras’ theorem.

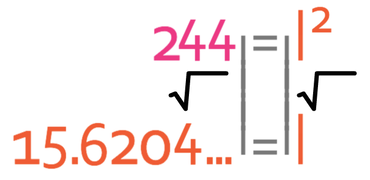
We want to find the value of l and not l2. Therefore, we square root both sides of the equation.

​Therefore, the slanted height of this cone is 15.6204… cm.
 
We are now able to work out the surface area of the cone because we know the radius (10 cm) and the slanted height (15.6204… cm)
The final step is to round to one decimal place. 

The total surface area of this cone is 804.9 cm2.