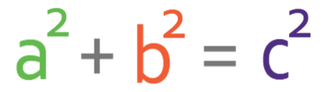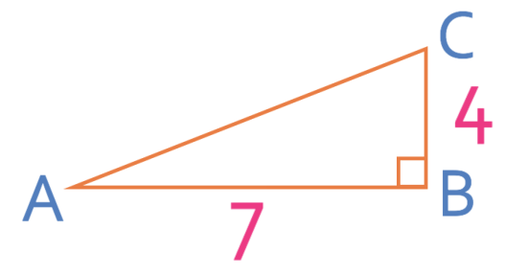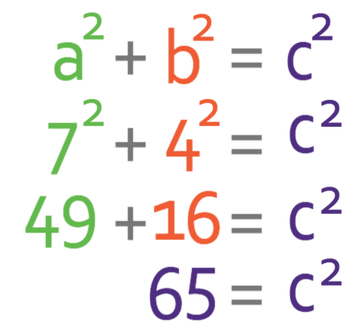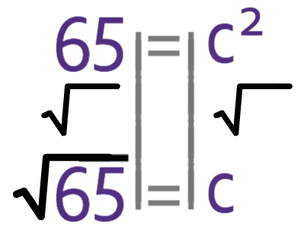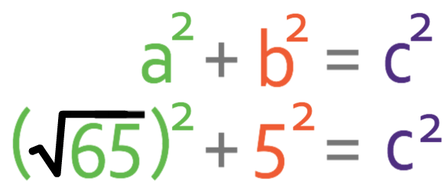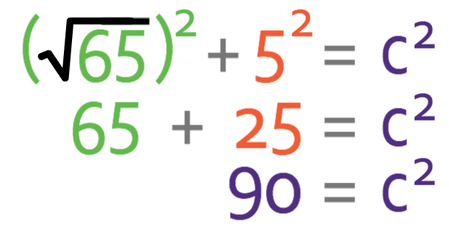Back to Edexcel Pythagoras’ Theorem (H) Home
4.9 E) Pythagoras 3D Shapes
4.9 E) Pythagoras 3D Shapes
Sometimes we will be asked to find the distance between different points in 3D shape by using Pythagoras’ theorem. We answer questions like this by creating right angled triangles within the 3D shape. It is worth looking at the formula for Pythagoras’ theorem before we have a look at an example. The formula for Pythagoras’ theorem is shown below:
c in the above formula is the hypotenuse, and a and b are the other two non-hypotenuse sides.
Example 1
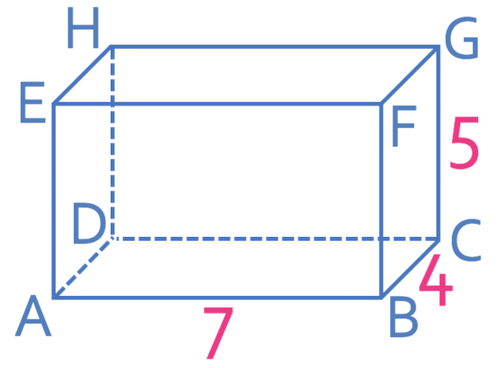
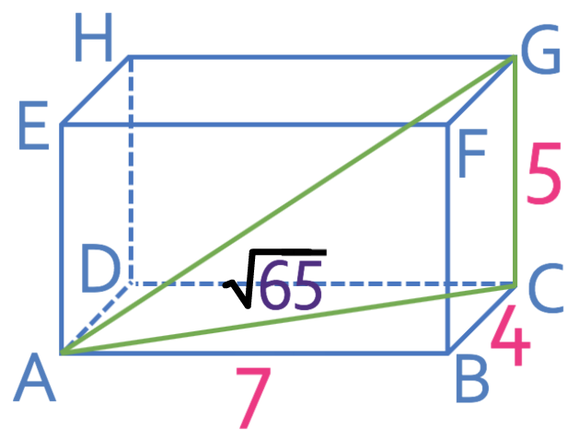
What is the distance between A and G? All of the values in the diagram below are in cm. Give you answer to one decimal place.
What is the distance between A and G? All of the values in the diagram below are in cm. Give you answer to one decimal place.
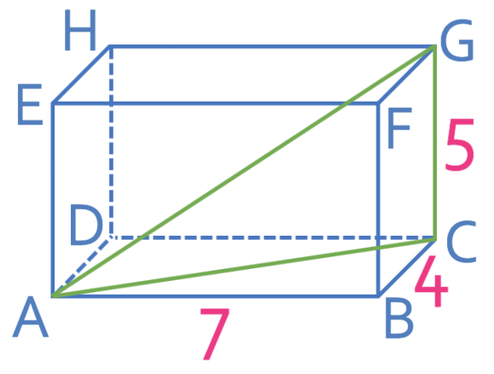
The question wants us to find what the distance is between A and G. We are going to be finding this distance by creating right-angled triangles. We can create a right-angled triangle between the point AGC. This triangle is drawn in green on the shape below.
However, we are unable to use this triangle to find the length of AG because we do not know what the length of AC is and this means that we have two unknown lengths, thus meaning that we cannot use Pythagoras’ theorem.
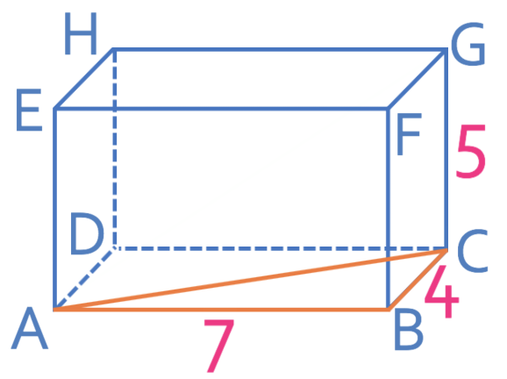
We are able to find the length of AC by creating another right-angled triangle. The second right-angled triangle will be ABC. We have the length AB and BC, which means that we can find the length AC. The triangle ABC is shown on the 3D shape in orange.
We are able to find the length of AC by creating another right-angled triangle. The second right-angled triangle will be ABC. We have the length AB and BC, which means that we can find the length AC. The triangle ABC is shown on the 3D shape in orange.
It is best to draw the right angle triangle that we are using out seperately. This is because it is so much easier to work with the triangle below rather than on the 3D shape.
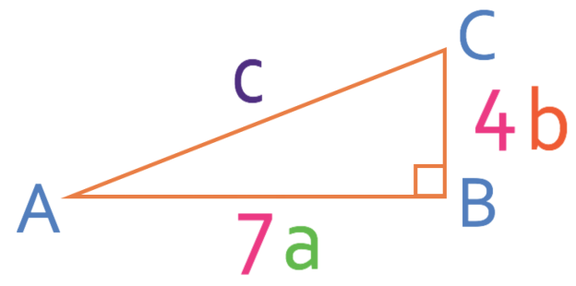
AC in this triangle is the hypotenuse, which means that it will be c. The other two non-hypotenuse sides are a and b. It does not matter which side is which; I am going to have a as 7 and b as 4.
The next step is to sub these values into Pythagoras’ theorem.
We want to find the value of c and not c2. Therefore, we square root both sides of the equation.
This is not our final answer, so it is best to keep the answer in exact form. Therefore, the length of AC is √65.
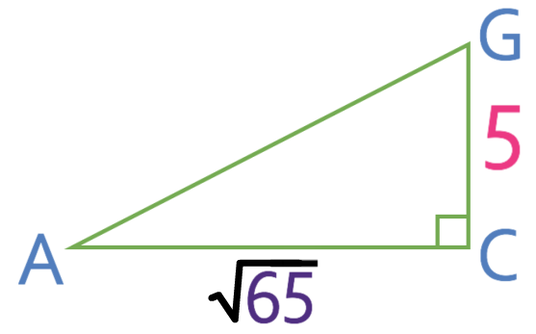
We now have the length of AC, which means we can find the length of AG by using the right-angle triangle AGC. This triangle is drawn in green on the 3D diagram below (I have added the length of AC to the diagram).
We now have the length of AC, which means we can find the length of AG by using the right-angle triangle AGC. This triangle is drawn in green on the 3D diagram below (I have added the length of AC to the diagram).
Like with the previous right angled triangle, it is best to draw this triangle out seperately.
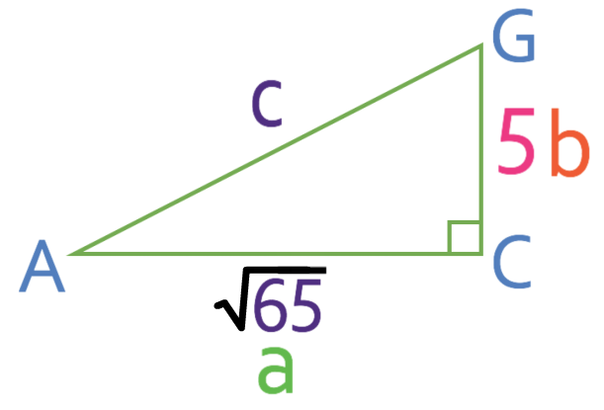
The hypotenuse of this right-angled triangle is AG, so I am going to label this side c. The other two non-hypotenuse sides are a and b, and it does not matter which is which; I am going to have AC as a (a is √65) and CG as b (b is 5).
We can sub these values into Pythagoras’ theorem to find the hypotenuse.
Squaring a square root gets rid of the square root, thus leaving the number that is inside the square root; √65 squared is 65.
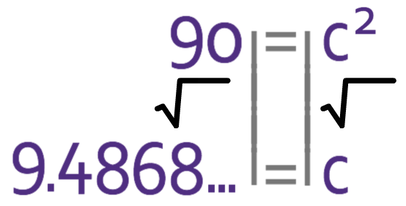
We want to find the value of c and not c2. Therefore, we square root both sides of the equation.
The final step is to round our answer to 1 decimal place.
Therefore, the distance between A and G is 9.5 cm.