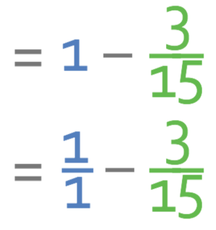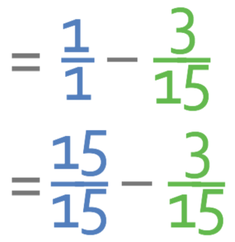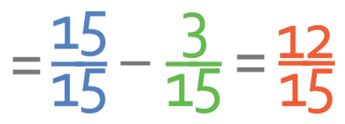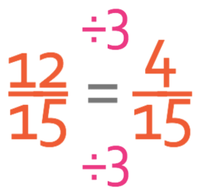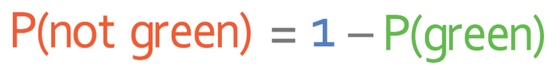5 D) Probability of an Event Not Happening
Example 1
A fridge contains 4 different flavoured yoghurts in the following quantities:
- 7 strawberry
- 1 apricot
- 3 blackcurrant
- 4 peach
What is the probability of not picking a blackcurrant yoghurt?
The first method is to use the following formula:
The denominator is the number of possible outcomes and we obtain this figure by finding the number of yoghurts that are in the fridge. There are 7 strawberry yoghurts, 1 apricot yoghurt, 3 blackcurrant yoghurts and 4 peach yoghurts. This means that there are 15 yoghurts in total, so the denominator is 15. Therefore, the probability of not picking a blackcurrant yoghurt is:
The probability of not picking a blackcurrant yoghurt is 4/5.
These events are mutually exclusive, which means that the event either does happen or does not happen; it cannot happen and not happen at the same time. This means that the probability that the event will happen and the probability that the event will not happen will add up to 1.
In order to use the equation above, we need to find out what the probability of the event happening is; in this case, we are looking for the probability of picking a blackcurrant yoghurt. There are 3 blackcurrant yoghurts and there are 15 yoghurts in total. This means that the probability of picking a blackcurrant yoghurt is 3/15. Let’s sub this into the equation.
As we are working with a fraction, it is easier if we convert the 1 in the equation to a fraction; I am going to write the 1 as 1/1.
When we are subtracting fractions, we need to make sure that the denominators of the fractions are the same. I am going to make the denominators of both fractions 15. This means that we multiply the numerator and denominator of the first fraction by 15 resulting in the fraction becoming 15/15.
A bag contains some balls. The probability of picking a green ball is 0.3. What is the probability of not picking a green ball?
We will only be able to answer this question by using the second method. The second method involves the formula below:
The formula to remember for working out the probability of an event not happening is given below.