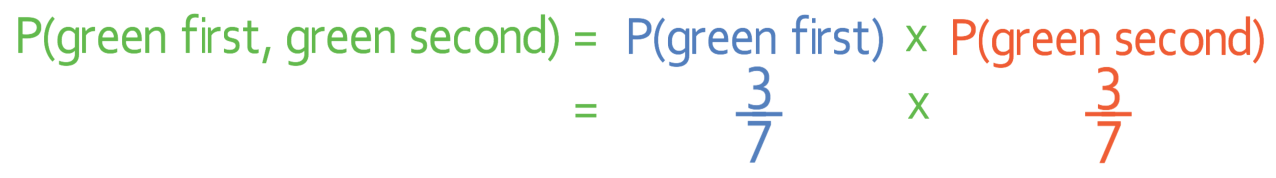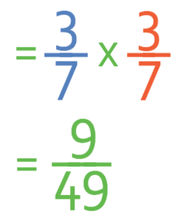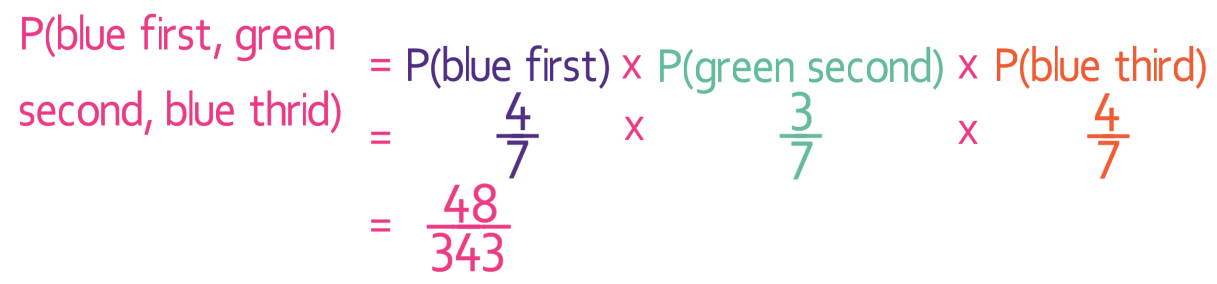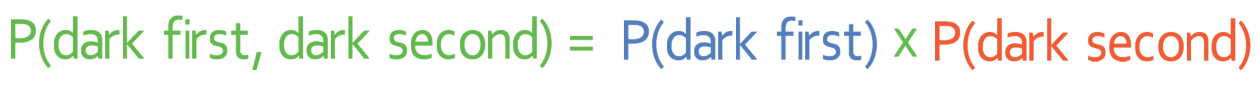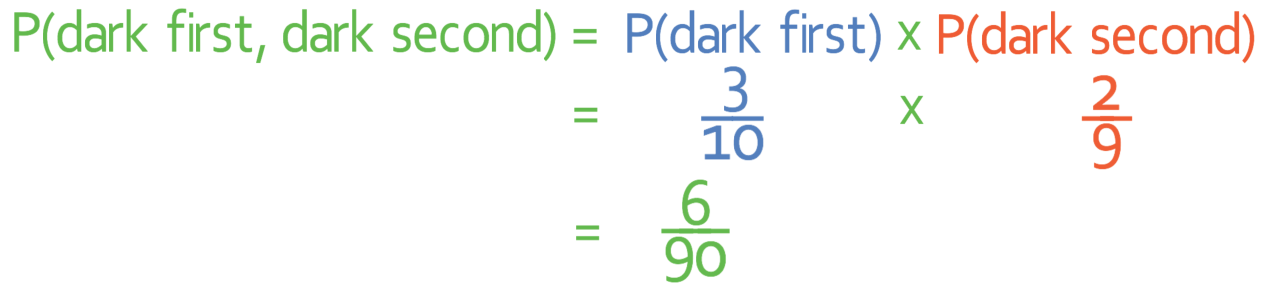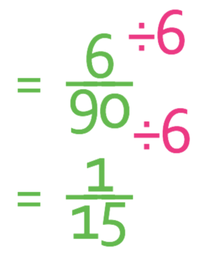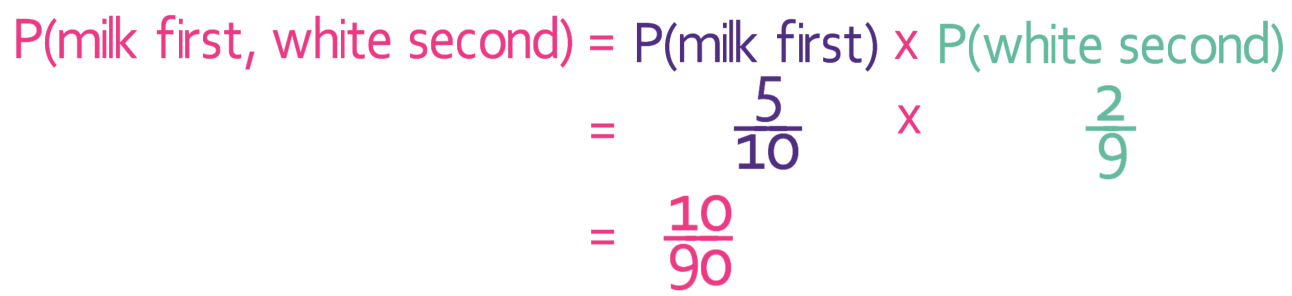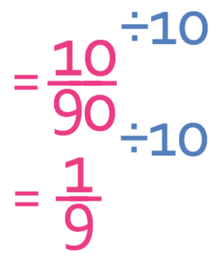Back to Edexcel Probability (H) Home
5 K) Combined Events – Probabilities: Part 2
The content in this section builds on the content in the previous section. Make sure that you have gone through the content in the previous section before working through the content in this section (click here to be taken through to the previous section). 
Example 1
A bag contains 7 balls; 3 of the balls are green and 4 of the balls are blue. Every time I pick a ball from the bag, I note the colour of the ball and then replace the ball back into the bag.
  1. I pick a ball from the bag twice. What is the probability that both of the balls are green?
  2. I pick a ball from the bag 3 times. What is the probability that the first ball is blue, the second ball is green, and the third ball is blue?
 
Part 1
We find the probability of picking two balls that are both green by multiplying the probability that the first ball is green by the probability that the second ball is green. 

In this example, the ball that has just been picked is replaced. This means that the probability that the first ball is green will be the same as the probability that the second ball is green. There are 3 green balls and 7 balls in total. This means that the probability of picking a green ball is 3/7 and this is the probability for both picking a green on the first pick and picking a green ball on the second pick.

When we are multiplying fraction, we multiply straight across; we multiply the numerators to obtain the numerator in the answer, and we multiply the denominators to obtain the denominator in the answer.

Therefore, the probability of picking a green ball on the first pick and also the second pick is 9/49.

 

Part 2

For part 2, we are looking for the probability that the first ball is blue, the second ball is green, and the third ball is blue. We obtain the answer by multiplying the probabilities for each of the three events together.

We already know what the probability of picking a green ball is (it is 3/7). The probability of picking a blue ball is 4/7 (there are 4 blue balls and 7 balls in total). As the balls are replaced, the probability of picking a blue ball on the first pick and on the third pick is the same. Let’s now sub these values into the equation above.  

Therefore, the probability of picking a blue ball first, a green ball second and a blue ball third is 48/343.

Example 2
A chocolate box contains 5 milk chocolates, 3 dark chocolates and 2 white chocolates. Whenever I take a chocolate from the box, I eat it, which means that the chocolate is not replaced.
  1. Work out the probability of picking a dark chocolate first and then another dark chocolate.
  2. Work out the probability of picking a milk chocolate and then a white chocolate.
 
Part 1
Part 1 asks us to find the probability of picking a dark chocolate and then another dark chocolate. In order to this this, we multiply the probability of picking a dark chocolate first by the probability of picking a dark chocolate second. 

When we are picking the first chocolate, there are 3 dark chocolates and 10 chocolates in total. This means that the probability of picking a dark chocolate on the first pick is 3/10.

 

After we pick a dark chocolate, the number of dark chocolates decreases by 1 and the total number of chocolates decreases by 1. This means that there are 2 dark chocolates left and 9 chocolates in total. Therefore, for the second pick, the probability of picking a dark chocolate is 2/9.

 

We can sub these values into the equation above to find the probability of picking two dark chocolates.

The final step is to check whether our fraction can be simplified. There is a common factor of 6 in the numerator and the denominator. Therefore, we simplify the fraction by dividing the numerator and the denominator by 6.

The probability is 1/15.

 

Part 2

Part 2 asks us to find the probability of choosing a milk chocolate and then a white chocolate. In order to find this probability, we multiply the probability of picking a milk chocolate first by the probability of picking a white chocolate second.

For the first pick, there are 10 chocolates in total and 5 of these chocolates are milk. This means that the probability of picking a milk chocolate on the first pick is 5/10.

 

After I have picked a milk chocolate, the total number of chocolates and the number of milk chocolates decreases by 1; there are now 9 chocolates in total and 4 milk chocolates. We are looking for the probability of choosing a white chocolate second. There are 2 white chocolates and 9 chocolates in total. This means that the probability of choosing a white chocolate second is 2/9. We can sub both of these probabilities into the equation above.

The final step is to simplify the fraction; we divide the numerator and the denominator by 10.

The probability of picking a milk chocolate first and then a white chocolate is 1/9.